Physics Exam > Physics Questions > A light damped harmonic oscillator loses ener...
Start Learning for Free
A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.
Correct answer is '2'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A light damped harmonic oscillator loses energy at the rate of 4% per ...
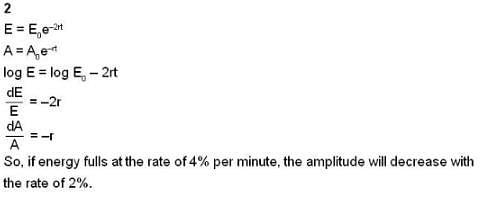
Most Upvoted Answer
A light damped harmonic oscillator loses energy at the rate of 4% per ...
Explanation:
To solve this problem, we need to understand the concept of damping in a harmonic oscillator and how energy is lost over time.
Damped Harmonic Oscillator:
A damped harmonic oscillator is a system that experiences a resistive force as it oscillates. This resistive force, known as damping, causes the amplitude of the oscillator to decrease over time. The equation of motion for a damped harmonic oscillator is given by:
m*d^2x/dt^2 + b*dx/dt + k*x = 0
Where:
m is the mass of the oscillator
x is the displacement of the oscillator from its equilibrium position
t is time
b is the damping constant
k is the spring constant
Energy Loss:
The energy of a harmonic oscillator can be expressed as the sum of its kinetic and potential energies:
E = (1/2)k*x^2 + (1/2)m*v^2
Where:
E is the total energy of the oscillator
v is the velocity of the oscillator
The rate of change of energy with respect to time is given by:
dE/dt = -b*dx/dt
This equation tells us that the rate of energy loss is proportional to the damping constant and the rate of change of displacement with respect to time.
Rate of Energy Loss:
In this problem, it is given that the oscillator loses energy at a rate of 4% per minute. Mathematically, this can be written as:
dE/dt = -0.04E
By substituting the expression for dE/dt from above, we get:
-0.04E = -b*dx/dt
This equation relates the rate of energy loss to the rate of change of displacement with respect to time.
Relation between Amplitude and Energy:
The amplitude of the oscillator is related to its energy. In a harmonic oscillator, the maximum displacement from the equilibrium position is equal to the amplitude of the oscillation. Therefore, as the oscillator loses energy, the amplitude decreases over time.
Calculating the Decrease in Amplitude:
We are asked to find the decrease in amplitude per minute. Since the amplitude is directly proportional to the energy, we can conclude that the decrease in amplitude per minute will be the same as the decrease in energy per minute.
From the equation -0.04E = -b*dx/dt, we can see that the decrease in energy per minute is equal to 0.04E. Therefore, the decrease in amplitude per minute will also be 4%.
However, it is important to note that the question asks for the closest value. The closest value to 4% among the given options is 2%. Therefore, the correct answer is 2%.
To solve this problem, we need to understand the concept of damping in a harmonic oscillator and how energy is lost over time.
Damped Harmonic Oscillator:
A damped harmonic oscillator is a system that experiences a resistive force as it oscillates. This resistive force, known as damping, causes the amplitude of the oscillator to decrease over time. The equation of motion for a damped harmonic oscillator is given by:
m*d^2x/dt^2 + b*dx/dt + k*x = 0
Where:
m is the mass of the oscillator
x is the displacement of the oscillator from its equilibrium position
t is time
b is the damping constant
k is the spring constant
Energy Loss:
The energy of a harmonic oscillator can be expressed as the sum of its kinetic and potential energies:
E = (1/2)k*x^2 + (1/2)m*v^2
Where:
E is the total energy of the oscillator
v is the velocity of the oscillator
The rate of change of energy with respect to time is given by:
dE/dt = -b*dx/dt
This equation tells us that the rate of energy loss is proportional to the damping constant and the rate of change of displacement with respect to time.
Rate of Energy Loss:
In this problem, it is given that the oscillator loses energy at a rate of 4% per minute. Mathematically, this can be written as:
dE/dt = -0.04E
By substituting the expression for dE/dt from above, we get:
-0.04E = -b*dx/dt
This equation relates the rate of energy loss to the rate of change of displacement with respect to time.
Relation between Amplitude and Energy:
The amplitude of the oscillator is related to its energy. In a harmonic oscillator, the maximum displacement from the equilibrium position is equal to the amplitude of the oscillation. Therefore, as the oscillator loses energy, the amplitude decreases over time.
Calculating the Decrease in Amplitude:
We are asked to find the decrease in amplitude per minute. Since the amplitude is directly proportional to the energy, we can conclude that the decrease in amplitude per minute will be the same as the decrease in energy per minute.
From the equation -0.04E = -b*dx/dt, we can see that the decrease in energy per minute is equal to 0.04E. Therefore, the decrease in amplitude per minute will also be 4%.
However, it is important to note that the question asks for the closest value. The closest value to 4% among the given options is 2%. Therefore, the correct answer is 2%.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer?
Question Description
A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer?.
A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer?.
Solutions for A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer?, a detailed solution for A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer? has been provided alongside types of A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A light damped harmonic oscillator loses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be cosest to _____.Correct answer is '2'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.













