Physics Exam > Physics Questions > An electron is moving inside a uniformly char...
Start Learning for Free
An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin of the charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .
- a)10-5 - 10-4 A0
- b)10-2 - 10-1 A0
- c)1 - 10 A0
- d)104 - 105 A0
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
An electron is moving inside a uniformly charged sphere with total cha...
Potential energy of interaction between electron and sphere
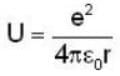
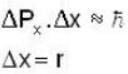
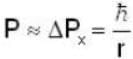
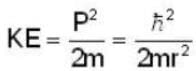
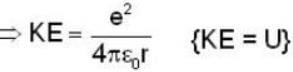
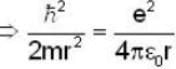
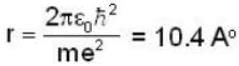
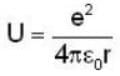
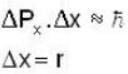
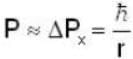
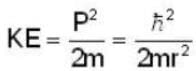
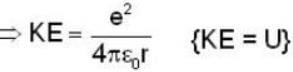
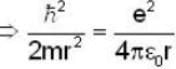
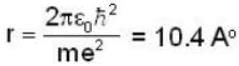
Most Upvoted Answer
An electron is moving inside a uniformly charged sphere with total cha...
States that the position and momentum of a particle cannot both be precisely determined at the same time. This means that there is an inherent uncertainty in the measurements of these properties.
In the case of the electron moving inside the uniformly charged sphere, the uncertainty principle implies that we cannot simultaneously know the exact position and momentum of the electron. This is because the electron's position and momentum are related through the uncertainty principle equation:
Δx * Δp ≥ h/4π
where Δx is the uncertainty in position, Δp is the uncertainty in momentum, and h is the Planck constant. The uncertainty principle sets a limit on how precisely we can know these properties.
In the context of the electron moving inside the uniformly charged sphere, this means that we cannot simultaneously know the exact position and momentum of the electron. The uncertainty in one property will necessarily lead to an uncertainty in the other property.
This uncertainty in position and momentum has important implications for the behavior of the electron. It means that the electron's motion cannot be precisely determined or predicted. Instead, we can only describe the electron's motion probabilistically, using wave functions and probability distributions.
Overall, the uncertainty principle implies that there are fundamental limits to our knowledge of the position and momentum of particles like electrons, and this has important consequences for our understanding of quantum mechanics.
In the case of the electron moving inside the uniformly charged sphere, the uncertainty principle implies that we cannot simultaneously know the exact position and momentum of the electron. This is because the electron's position and momentum are related through the uncertainty principle equation:
Δx * Δp ≥ h/4π
where Δx is the uncertainty in position, Δp is the uncertainty in momentum, and h is the Planck constant. The uncertainty principle sets a limit on how precisely we can know these properties.
In the context of the electron moving inside the uniformly charged sphere, this means that we cannot simultaneously know the exact position and momentum of the electron. The uncertainty in one property will necessarily lead to an uncertainty in the other property.
This uncertainty in position and momentum has important implications for the behavior of the electron. It means that the electron's motion cannot be precisely determined or predicted. Instead, we can only describe the electron's motion probabilistically, using wave functions and probability distributions.
Overall, the uncertainty principle implies that there are fundamental limits to our knowledge of the position and momentum of particles like electrons, and this has important consequences for our understanding of quantum mechanics.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer?
Question Description
An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer?.
An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer?.
Solutions for An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer?, a detailed solution for An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An electron is moving inside a uniformly charged sphere with total charge +ve. The uncertainty principle ΔPxΔx ≥ n is used for finding the smallest radius rmin ofthe charged sphere such that the kinetic energy of the electron is equal to its potential energy on the surface of the sphere. The rmin is approximately in the range .a)10-5 - 10-4 A0b)10-2 - 10-1 A0c)1 - 10 A0d)104 - 105 A0Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















