Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Questions > A signal x(t) = 100 cos (24p x 103t) is ideal...
Start Learning for Free
A signal x(t) = 100 cos (24
p
x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?- a)12 kHz only
- b)8 kHz only
- c)12 kHz and 9 kHz
- d)12 kHz and 8 kHz
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a samplin...
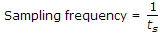
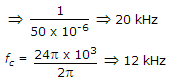
Frequency pass by L.P.F. are, fc fs - fc
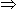 12 kHz, 8 kHz.
12 kHz, 8 kHz.Most Upvoted Answer
A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a samplin...
Sampling of Signal x(t)
- The signal x(t) = 100 cos (24π × 10^3t) is sampled with a sampling period of 50 μs.
- The sampling frequency is given by fs = 1/Ts, where Ts is the sampling period.
- Therefore, fs = 1/50 μs = 20 kHz.
- According to the Nyquist sampling theorem, the signal can be reconstructed perfectly if the sampling frequency is at least twice the highest frequency component of the signal.
- The highest frequency component of x(t) is 24π × 10^3 Hz, which is less than half of the sampling frequency of 20 kHz.
- Hence, the sampling is ideal and there is no aliasing.
Filtering of Sampled Signal
- The sampled signal can be expressed as x(nTs) = 100 cos (24π × 10^3nTs), where n is an integer.
- The sampled signal is passed through an ideal low-pass filter with a cutoff frequency of 15 kHz.
- The frequency response of the ideal low-pass filter is given by H(f) = 1 for |f| ≤ 15 kHz and H(f) = 0 for |f| > 15 kHz.
- The output of the filter can be obtained by convolving the input signal with the impulse response of the filter, which is a sinc function.
- The Fourier transform of the sinc function is a rectangular function, which is equal to 1 for frequencies between -fc and fc, and zero otherwise.
- Therefore, the output of the filter will be the product of the Fourier transforms of the input signal and the filter impulse response.
Calculation of Filter Output Frequencies
- The Fourier transform of the sampled signal x(nTs) is given by X(f) = 0.5[δ(f - fs) + δ(f + fs)] * Xc(f), where Xc(f) is the Fourier transform of the continuous-time signal x(t).
- The Fourier transform of the ideal low-pass filter impulse response is given by H(f) = rect(f/2fc), where fc is the cutoff frequency.
- Therefore, the Fourier transform of the filter output can be obtained as Y(f) = X(f) * H(f), where * denotes convolution.
- Substituting the expressions for X(f) and H(f), we get Y(f) = 0.5[rect((f - fs)/2fc) + rect((f + fs)/2fc)] * Xc(f).
- The rectangular functions can be simplified using the identity rect(a)rect(b) = rect(min(a, b)).
- Therefore, Y(f) = rect((f - fs)/2fc) * Xc(f) for |f - fs| ≤ fc, and Y(f) = rect((f + fs)/2fc) * Xc(f) for |f + fs| ≤ fc.
- Substituting the values of fs and fc, we get Y(f) = rect((f - 20 kHz)/30 kHz) * Xc(f) for 5 kHz ≤ f ≤ 35 kHz, and Y(f) = rect((f + 20 kHz)/30 kHz) * Xc(f) for -35 kHz ≤ f ≤ -5 kHz.
- The Fourier transform of the filter output can be inverse-transformed to obtain the time-domain signal.
- The time
- The signal x(t) = 100 cos (24π × 10^3t) is sampled with a sampling period of 50 μs.
- The sampling frequency is given by fs = 1/Ts, where Ts is the sampling period.
- Therefore, fs = 1/50 μs = 20 kHz.
- According to the Nyquist sampling theorem, the signal can be reconstructed perfectly if the sampling frequency is at least twice the highest frequency component of the signal.
- The highest frequency component of x(t) is 24π × 10^3 Hz, which is less than half of the sampling frequency of 20 kHz.
- Hence, the sampling is ideal and there is no aliasing.
Filtering of Sampled Signal
- The sampled signal can be expressed as x(nTs) = 100 cos (24π × 10^3nTs), where n is an integer.
- The sampled signal is passed through an ideal low-pass filter with a cutoff frequency of 15 kHz.
- The frequency response of the ideal low-pass filter is given by H(f) = 1 for |f| ≤ 15 kHz and H(f) = 0 for |f| > 15 kHz.
- The output of the filter can be obtained by convolving the input signal with the impulse response of the filter, which is a sinc function.
- The Fourier transform of the sinc function is a rectangular function, which is equal to 1 for frequencies between -fc and fc, and zero otherwise.
- Therefore, the output of the filter will be the product of the Fourier transforms of the input signal and the filter impulse response.
Calculation of Filter Output Frequencies
- The Fourier transform of the sampled signal x(nTs) is given by X(f) = 0.5[δ(f - fs) + δ(f + fs)] * Xc(f), where Xc(f) is the Fourier transform of the continuous-time signal x(t).
- The Fourier transform of the ideal low-pass filter impulse response is given by H(f) = rect(f/2fc), where fc is the cutoff frequency.
- Therefore, the Fourier transform of the filter output can be obtained as Y(f) = X(f) * H(f), where * denotes convolution.
- Substituting the expressions for X(f) and H(f), we get Y(f) = 0.5[rect((f - fs)/2fc) + rect((f + fs)/2fc)] * Xc(f).
- The rectangular functions can be simplified using the identity rect(a)rect(b) = rect(min(a, b)).
- Therefore, Y(f) = rect((f - fs)/2fc) * Xc(f) for |f - fs| ≤ fc, and Y(f) = rect((f + fs)/2fc) * Xc(f) for |f + fs| ≤ fc.
- Substituting the values of fs and fc, we get Y(f) = rect((f - 20 kHz)/30 kHz) * Xc(f) for 5 kHz ≤ f ≤ 35 kHz, and Y(f) = rect((f + 20 kHz)/30 kHz) * Xc(f) for -35 kHz ≤ f ≤ -5 kHz.
- The Fourier transform of the filter output can be inverse-transformed to obtain the time-domain signal.
- The time
Attention Electronics and Communication Engineering (ECE) Students!
To make sure you are not studying endlessly, EduRev has designed Electronics and Communication Engineering (ECE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Electronics and Communication Engineering (ECE).

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Similar Electronics and Communication Engineering (ECE) Doubts
A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer?
Question Description
A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2024 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer?.
A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2024 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer?.
Solutions for A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electronics and Communication Engineering (ECE).
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Here you can find the meaning of A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A signal x(t) = 100 cos (24p x 103t) is ideally sampled with a sampling period of 50 μ sec and then passed through an ideal low pass filter with cut off frequency of 15 kHz Which of the following frequencies are present at the filter output?a)12 kHz onlyb)8 kHz onlyc)12 kHz and 9 kHzd)12 kHz and 8 kHzCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Electronics and Communication Engineering (ECE) tests.

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























