Physics Exam > Physics Questions > The solution to the Schrodinger equation for ...
Start Learning for Free
The solution to the Schrodinger equation for a particle bound in a one-dimensional, infinitely deep potential well, indexed by a quantum number n, indicates that in the middle of the well, the probability density vanishes for.
- a)all states except the ground state
- b)states of even n(n = 2, 4...)
- c)Ground state (n = 1) only.
- d)states of odd n(n = 1, 2, 3...)
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The solution to the Schrodinger equation for a particle bound inaone-d...
For particle in a box
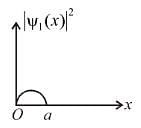
For ψ1(x), probability density does not vanish in the middle
for
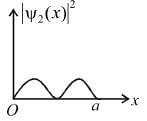
for

probability density vanishes in the middle
Similarly, it does not vanish for 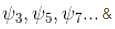 vanishes for
vanishes for  in the middle of the well.
in the middle of the well.
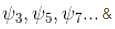 vanishes for
vanishes for  in the middle of the well.
in the middle of the well.The correct answer is: states of even n(n = 2, 4...)
Most Upvoted Answer
The solution to the Schrodinger equation for a particle bound inaone-d...
Solution to the Schrodinger equation for a particle bound in a one-dimensional, infinitely deep potential well
The Schrodinger equation is a fundamental equation in quantum mechanics that describes the behavior of particles in terms of wave functions. When a particle is bound in a one-dimensional, infinitely deep potential well, the Schrodinger equation can be solved to determine the wave function and the corresponding probability density.
Understanding the potential well
In a one-dimensional, infinitely deep potential well, the particle is confined to a finite region. The potential energy inside the well is zero, while outside the well it is infinite. This means that the particle cannot escape from the well. The potential well can be visualized as a box with impenetrable walls.
Solving the Schrodinger equation
The Schrodinger equation for a particle in a one-dimensional, infinitely deep potential well is given by:
Hψ = Eψ
Here, H is the Hamiltonian operator, ψ is the wave function, E is the energy, and ħ is the reduced Planck's constant.
Solving this equation involves finding the wave function ψ and the corresponding energy E. The solution to the Schrodinger equation yields a set of quantized energy levels, indexed by a quantum number n.
Probabilty density in the middle of the well
In the middle of the potential well, the probability density is given by |ψ|^2, where |ψ| represents the modulus squared of the wave function ψ.
The wave function for a particle in a one-dimensional, infinitely deep potential well is given by:
ψ(x) = √(2/L)sin(nπx/L)
Here, L is the length of the well, x is the position coordinate, and n is the quantum number.
When n is even (n = 2, 4, ...), the wave function ψ(x) is an odd function. This means that ψ(x) changes sign when x is reflected about the center of the well. As a result, the probability density |ψ|^2 is symmetric about the center of the well and vanishes at the center. This is because the positive and negative contributions to the probability density from the wave function cancel each other out.
On the other hand, when n is odd (n = 1, 3, ...), the wave function ψ(x) is an even function. This means that ψ(x) remains unchanged when x is reflected about the center of the well. As a result, the probability density |ψ|^2 is anti-symmetric about the center of the well and does not vanish at the center.
Therefore, the solution to the Schrodinger equation indicates that in the middle of the well, the probability density vanishes for states of even n (n = 2, 4, ...), but does not vanish for states of odd n (n = 1, 3, ...).
In conclusion
The solution to the Schrodinger equation for a particle bound in a one-dimensional, infinitely deep potential well indicates that in the middle of the well, the probability density vanishes for states of even n (n = 2, 4, ...), while it does not vanish for states of odd n (n = 1, 3, ...). This is because the wave function
The Schrodinger equation is a fundamental equation in quantum mechanics that describes the behavior of particles in terms of wave functions. When a particle is bound in a one-dimensional, infinitely deep potential well, the Schrodinger equation can be solved to determine the wave function and the corresponding probability density.
Understanding the potential well
In a one-dimensional, infinitely deep potential well, the particle is confined to a finite region. The potential energy inside the well is zero, while outside the well it is infinite. This means that the particle cannot escape from the well. The potential well can be visualized as a box with impenetrable walls.
Solving the Schrodinger equation
The Schrodinger equation for a particle in a one-dimensional, infinitely deep potential well is given by:
Hψ = Eψ
Here, H is the Hamiltonian operator, ψ is the wave function, E is the energy, and ħ is the reduced Planck's constant.
Solving this equation involves finding the wave function ψ and the corresponding energy E. The solution to the Schrodinger equation yields a set of quantized energy levels, indexed by a quantum number n.
Probabilty density in the middle of the well
In the middle of the potential well, the probability density is given by |ψ|^2, where |ψ| represents the modulus squared of the wave function ψ.
The wave function for a particle in a one-dimensional, infinitely deep potential well is given by:
ψ(x) = √(2/L)sin(nπx/L)
Here, L is the length of the well, x is the position coordinate, and n is the quantum number.
When n is even (n = 2, 4, ...), the wave function ψ(x) is an odd function. This means that ψ(x) changes sign when x is reflected about the center of the well. As a result, the probability density |ψ|^2 is symmetric about the center of the well and vanishes at the center. This is because the positive and negative contributions to the probability density from the wave function cancel each other out.
On the other hand, when n is odd (n = 1, 3, ...), the wave function ψ(x) is an even function. This means that ψ(x) remains unchanged when x is reflected about the center of the well. As a result, the probability density |ψ|^2 is anti-symmetric about the center of the well and does not vanish at the center.
Therefore, the solution to the Schrodinger equation indicates that in the middle of the well, the probability density vanishes for states of even n (n = 2, 4, ...), but does not vanish for states of odd n (n = 1, 3, ...).
In conclusion
The solution to the Schrodinger equation for a particle bound in a one-dimensional, infinitely deep potential well indicates that in the middle of the well, the probability density vanishes for states of even n (n = 2, 4, ...), while it does not vanish for states of odd n (n = 1, 3, ...). This is because the wave function
Free Test
FREE
| Start Free Test |
Community Answer
The solution to the Schrodinger equation for a particle bound inaone-d...
For particle in a box

For ψ1(x), probability density does not vanish in the middle
for

for

probability density vanishes in the middle
Similarly, it does not vanish for 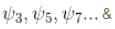 vanishes for
vanishes for 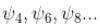 in the middle of the well.
in the middle of the well.
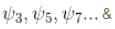 vanishes for
vanishes for 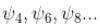 in the middle of the well.
in the middle of the well.The correct answer is: states of even n(n = 2, 4...)

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer?
Question Description
The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer?.
The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer?.
Solutions for The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer?, a detailed solution for The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The solution to the Schrodinger equation for a particle bound inaone-dimensional, infinitely deep potential well, indexed by a quantum numbern, indicates that in the middle of the well, the probability density vanishes for.a)all states except the ground stateb)states of evenn(n= 2, 4...)c)Ground state (n= 1) only.d)states of oddn(n= 1, 2, 3...)Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















