Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > For 64 bit virtual addresses, a 4 KB page siz...
Start Learning for Free
For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requires
- a)240 entries
- b)252 entries
- c)216 entries
- d)278 entries
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an i...
Virtul address space = 264 bytes
Page size = 4 KB
= 212 Bytes
Physical Memotry = 256 MB.
= 228 Bytes
Number of entries in inverted page table = Number of frames in physical memory
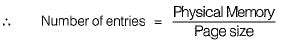
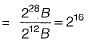
Page size = 4 KB
= 212 Bytes
Physical Memotry = 256 MB.
= 228 Bytes
Number of entries in inverted page table = Number of frames in physical memory
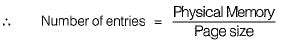
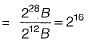
Most Upvoted Answer
For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an i...
Explanation:
An inverted page table is a data structure used by the operating system to keep track of which virtual addresses are mapped to which physical addresses. In an inverted page table, instead of each process having its own page table, there is a single table that maps physical addresses to virtual addresses.
Given:
- 64 bit virtual addresses
- 4 KB page size
- 256 MB of RAM
To calculate the number of entries required for an inverted page table, we need to consider the following:
1. Virtual address space:
- 64 bit virtual addresses allow for a maximum of 2^64 possible addresses.
- Since the page size is 4 KB, each page can hold 2^12 bytes of memory.
- Therefore, the virtual address space can be divided into 2^64 / 2^12 = 2^52 pages.
2. Physical address space:
- There is 256 MB of RAM available.
- Since the page size is 4 KB, the physical address space can be divided into 256 MB / 4 KB = 2^18 pages.
3. Inverted page table:
- In an inverted page table, each entry corresponds to a physical page frame.
- Since there are 2^18 physical page frames available, the inverted page table requires 2^18 entries.
4. Hash table:
- Since the number of virtual pages (2^52) is much larger than the number of physical pages (2^18), a hash table is used to map virtual pages to physical page frames.
- The size of the hash table depends on the number of entries in the inverted page table.
- A commonly used formula for the size of the hash table is:
size of hash table = (number of entries in inverted page table) / 0.7
- Using this formula, the size of the hash table for our case is:
size of hash table = 2^18 / 0.7 = 245760.87
- Since the size of a hash table must be a power of 2, the next larger power of 2 is 2^18.
Therefore, the inverted page table requires 2^18 entries, or 262144 (216) entries.
An inverted page table is a data structure used by the operating system to keep track of which virtual addresses are mapped to which physical addresses. In an inverted page table, instead of each process having its own page table, there is a single table that maps physical addresses to virtual addresses.
Given:
- 64 bit virtual addresses
- 4 KB page size
- 256 MB of RAM
To calculate the number of entries required for an inverted page table, we need to consider the following:
1. Virtual address space:
- 64 bit virtual addresses allow for a maximum of 2^64 possible addresses.
- Since the page size is 4 KB, each page can hold 2^12 bytes of memory.
- Therefore, the virtual address space can be divided into 2^64 / 2^12 = 2^52 pages.
2. Physical address space:
- There is 256 MB of RAM available.
- Since the page size is 4 KB, the physical address space can be divided into 256 MB / 4 KB = 2^18 pages.
3. Inverted page table:
- In an inverted page table, each entry corresponds to a physical page frame.
- Since there are 2^18 physical page frames available, the inverted page table requires 2^18 entries.
4. Hash table:
- Since the number of virtual pages (2^52) is much larger than the number of physical pages (2^18), a hash table is used to map virtual pages to physical page frames.
- The size of the hash table depends on the number of entries in the inverted page table.
- A commonly used formula for the size of the hash table is:
size of hash table = (number of entries in inverted page table) / 0.7
- Using this formula, the size of the hash table for our case is:
size of hash table = 2^18 / 0.7 = 245760.87
- Since the size of a hash table must be a power of 2, the next larger power of 2 is 2^18.
Therefore, the inverted page table requires 2^18 entries, or 262144 (216) entries.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Similar Computer Science Engineering (CSE) Doubts
For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer?
Question Description
For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer?.
For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer?.
Solutions for For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice For 64 bit virtual addresses, a 4 KB page size and 256 MB of RAM, an inverted page table requiresa)240 entriesb)252 entriesc)216 entriesd)278 entriesCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























