Physics Exam > Physics Questions > An ideal gas having initial pressure P, volum...
Start Learning for Free
An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?
Select one:
Select one:
- a)10
- b)7
- c)5
- d)3
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
An ideal gas having initial pressure P, volume V and temperature T is ...
In adiabatic process 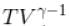 = constant
= constant
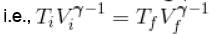
Here,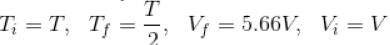
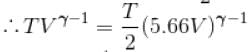
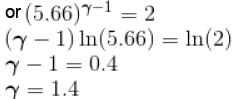
We know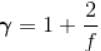
Here f = degree of freedom
So, putting the value of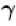
f = 5
The correct answer is: 5
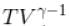 = constant
= constant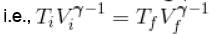
Here,
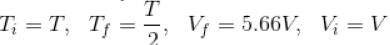
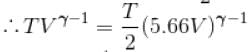
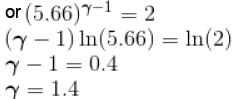
We know
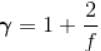
Here f = degree of freedom
So, putting the value of
f = 5
The correct answer is: 5
Free Test
FREE
| Start Free Test |
Community Answer
An ideal gas having initial pressure P, volume V and temperature T is ...
Gas molecules have three degrees of freedom for translational motion along the x, y, and z directions. Additionally, for a diatomic gas molecule, there are two more degrees of freedom for rotational motion. Therefore, the total number of degrees of freedom for a diatomic gas molecule is five.
For an ideal gas, the internal energy depends only on temperature and is given by the equation:
U = (f/2) * N * k * T
where U is the internal energy, f is the number of degrees of freedom, N is the number of gas molecules, k is the Boltzmann constant, and T is the temperature.
Since the gas is expanding adiabatically, there is no heat exchange with the surroundings, and the process is reversible. In an adiabatic expansion, the relationship between pressure (P), volume (V), and temperature (T) is given by:
PV^(gamma) = constant
where gamma is the ratio of specific heat capacities (Cp/Cv) for the gas.
In this case, the volume increases to 5.66V and the temperature decreases. Therefore, using the adiabatic expansion formula, we can write:
(P * V^gamma) / T = constant
Since the initial and final states of the gas are known, we can use the above equation to find the new temperature (T') at the final volume (5.66V).
Now, let's consider the initial and final states of the gas:
Initial state:
Pressure = P
Volume = V
Temperature = T
Final state:
Pressure = ?
Volume = 5.66V
Temperature = T'
Using the adiabatic expansion formula, we can write:
(P * V^gamma) / T = (P' * (5.66V)^gamma) / T'
Since the process is adiabatic, the initial and final pressures can be related using the ideal gas law equation:
P * V = P' * (5.66V)
Simplifying the equation:
P' = (P * V) / (5.66V)
P' = P / 5.66
Substituting this value of P' into the adiabatic expansion formula:
(P * V^gamma) / T = (P / 5.66 * (5.66V)^gamma) / T'
Simplifying the equation:
V^gamma / T = (1 / 5.66 * (5.66V)^gamma) / T'
V^gamma / T = V^gamma / (5.66 * T')
Since the initial and final volumes are not equal to zero, we can cancel out V^gamma from both sides of the equation:
1 / T = 1 / (5.66 * T')
Solving for T':
T' = 5.66 * T
Therefore, the final temperature is 5.66 times the initial temperature.
Since the temperature has changed, but the gas molecules have not gained or lost any degrees of freedom, the number of degrees of freedom for the gas molecules remains the same. Thus, the gas molecules still have five degrees of freedom.
Therefore, the correct answer is option C) 5.
For an ideal gas, the internal energy depends only on temperature and is given by the equation:
U = (f/2) * N * k * T
where U is the internal energy, f is the number of degrees of freedom, N is the number of gas molecules, k is the Boltzmann constant, and T is the temperature.
Since the gas is expanding adiabatically, there is no heat exchange with the surroundings, and the process is reversible. In an adiabatic expansion, the relationship between pressure (P), volume (V), and temperature (T) is given by:
PV^(gamma) = constant
where gamma is the ratio of specific heat capacities (Cp/Cv) for the gas.
In this case, the volume increases to 5.66V and the temperature decreases. Therefore, using the adiabatic expansion formula, we can write:
(P * V^gamma) / T = constant
Since the initial and final states of the gas are known, we can use the above equation to find the new temperature (T') at the final volume (5.66V).
Now, let's consider the initial and final states of the gas:
Initial state:
Pressure = P
Volume = V
Temperature = T
Final state:
Pressure = ?
Volume = 5.66V
Temperature = T'
Using the adiabatic expansion formula, we can write:
(P * V^gamma) / T = (P' * (5.66V)^gamma) / T'
Since the process is adiabatic, the initial and final pressures can be related using the ideal gas law equation:
P * V = P' * (5.66V)
Simplifying the equation:
P' = (P * V) / (5.66V)
P' = P / 5.66
Substituting this value of P' into the adiabatic expansion formula:
(P * V^gamma) / T = (P / 5.66 * (5.66V)^gamma) / T'
Simplifying the equation:
V^gamma / T = (1 / 5.66 * (5.66V)^gamma) / T'
V^gamma / T = V^gamma / (5.66 * T')
Since the initial and final volumes are not equal to zero, we can cancel out V^gamma from both sides of the equation:
1 / T = 1 / (5.66 * T')
Solving for T':
T' = 5.66 * T
Therefore, the final temperature is 5.66 times the initial temperature.
Since the temperature has changed, but the gas molecules have not gained or lost any degrees of freedom, the number of degrees of freedom for the gas molecules remains the same. Thus, the gas molecules still have five degrees of freedom.
Therefore, the correct answer is option C) 5.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer?
Question Description
An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer?.
An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer?.
Solutions for An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer?, a detailed solution for An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An ideal gas having initial pressure P, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V and its temperature falls to How many degree of freedom do gas molecule have?Select one:a)10b)7c)5d)3Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
















