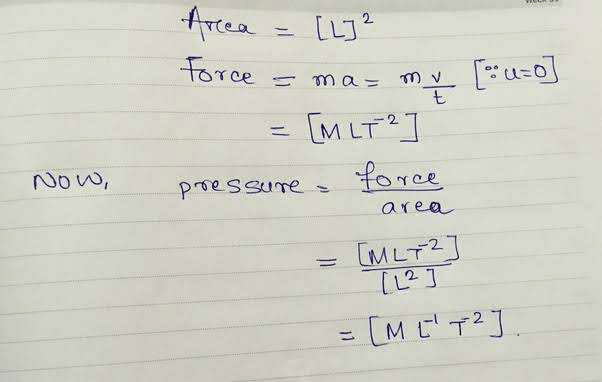Class 10 Exam > Class 10 Questions > Dimensional formula of pressure?
Start Learning for Free
Dimensional formula of pressure?
Community Answer
Dimensional formula of pressure?
Definition of Pressure
Pressure is defined as the force exerted per unit area. It is a scalar quantity and is expressed in units of pascal (Pa).
Dimensional Formula of Pressure
The dimensional formula of pressure is [M L^-1 T^-2], which means that pressure is directly proportional to the force applied and inversely proportional to the area over which the force is applied.
Explanation
To understand the dimensional formula of pressure, let's break it down into its fundamental dimensions:
- [M] stands for mass, which represents the amount of matter in an object.
- [L^-1] stands for length raised to the power of negative one, which represents the inverse of distance. This dimension is used to express area, which is the amount of space enclosed by a two-dimensional shape.
- [T^-2] stands for time raised to the power of negative two, which represents the inverse of time squared. This dimension is used to express acceleration, which is the rate of change of velocity over time.
When we combine these dimensions, we get [M L^-1 T^-2], which represents the dimensional formula of pressure. This formula shows that pressure is directly proportional to the force applied (which has the dimension [M L T^-2]) and inversely proportional to the area over which the force is applied (which has the dimension [L^2]).
Conclusion
In summary, the dimensional formula of pressure is [M L^-1 T^-2], which represents the relationship between force, area, and time. Understanding the dimensional formula of pressure can help us better understand the physical properties of pressure and how it relates to other quantities in physics.
Pressure is defined as the force exerted per unit area. It is a scalar quantity and is expressed in units of pascal (Pa).
Dimensional Formula of Pressure
The dimensional formula of pressure is [M L^-1 T^-2], which means that pressure is directly proportional to the force applied and inversely proportional to the area over which the force is applied.
Explanation
To understand the dimensional formula of pressure, let's break it down into its fundamental dimensions:
- [M] stands for mass, which represents the amount of matter in an object.
- [L^-1] stands for length raised to the power of negative one, which represents the inverse of distance. This dimension is used to express area, which is the amount of space enclosed by a two-dimensional shape.
- [T^-2] stands for time raised to the power of negative two, which represents the inverse of time squared. This dimension is used to express acceleration, which is the rate of change of velocity over time.
When we combine these dimensions, we get [M L^-1 T^-2], which represents the dimensional formula of pressure. This formula shows that pressure is directly proportional to the force applied (which has the dimension [M L T^-2]) and inversely proportional to the area over which the force is applied (which has the dimension [L^2]).
Conclusion
In summary, the dimensional formula of pressure is [M L^-1 T^-2], which represents the relationship between force, area, and time. Understanding the dimensional formula of pressure can help us better understand the physical properties of pressure and how it relates to other quantities in physics.

|
Explore Courses for Class 10 exam
|

|
Similar Class 10 Doubts
Dimensional formula of pressure?
Question Description
Dimensional formula of pressure? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about Dimensional formula of pressure? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Dimensional formula of pressure?.
Dimensional formula of pressure? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about Dimensional formula of pressure? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Dimensional formula of pressure?.
Solutions for Dimensional formula of pressure? in English & in Hindi are available as part of our courses for Class 10.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Here you can find the meaning of Dimensional formula of pressure? defined & explained in the simplest way possible. Besides giving the explanation of
Dimensional formula of pressure?, a detailed solution for Dimensional formula of pressure? has been provided alongside types of Dimensional formula of pressure? theory, EduRev gives you an
ample number of questions to practice Dimensional formula of pressure? tests, examples and also practice Class 10 tests.

|
Explore Courses for Class 10 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.