Mathematics Exam > Mathematics Questions > The degree of a differential equation is defi...
Start Learning for Free
The degree of a differential equation is defined as the
- a)Highest of the orders of the differential coefficients occuring in it
- b)Highest power of the highest order differential coefficient occurring in it
- c)Any power of the highest order differential coefficient occurring in it
- d)Highest power among the powers of the dif ferential coefficients occurring in it
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The degree of a differential equation is defined as thea)Highest of th...
Definition : The degree of a differential equation is defined as the highest power of the highest order derivative involved in the differential, where the equation has been made rational and integral as far as the derivatives are concerned.
degree of DE (1) = 2
degree of DE (2) = 1
degree of DE (3) = 1
An Important Example : Find the degree of the differential equation.
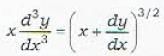
In order to rationalize this equation, we first square this equation and get
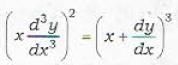
Now clearly the degree of the differential equation is 2.
Thus statement (b) gives the correct definition of the degee of a differential equation.
degree of DE (1) = 2
degree of DE (2) = 1
degree of DE (3) = 1
An Important Example : Find the degree of the differential equation.
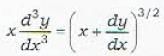
In order to rationalize this equation, we first square this equation and get
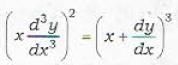
Now clearly the degree of the differential equation is 2.
Thus statement (b) gives the correct definition of the degee of a differential equation.
Most Upvoted Answer
The degree of a differential equation is defined as thea)Highest of th...
Explanation:
The degree of a differential equation is a measure of the highest power of the highest order derivative that appears in the equation. It helps us classify the type of differential equation and determine the appropriate methods for solving it.
Degree of a differential equation:
The degree of a differential equation is determined by the highest power of the highest order derivative present in the equation. In other words, it is the power to which the highest order derivative is raised.
Let's consider an example to understand this concept better:
Example:
Consider the following differential equation:
dy/dx + 3y^2 + 2x = 0
In this equation, the highest order derivative is dy/dx, and it is raised to the power of 1. Therefore, the degree of this differential equation is 1.
Another example:
Example:
Consider the following differential equation:
d^3y/dx^3 + 5(dy/dx)^2 + 2x = 0
In this equation, the highest order derivative is d^3y/dx^3, and it is raised to the power of 1. Therefore, the degree of this differential equation is 1.
Why is the answer option 'B'?
In the given options, option 'B' correctly defines the degree of a differential equation as the highest power of the highest order differential coefficient occurring in it. It aligns with the concept discussed above, where the degree is determined by the highest power to which the highest order derivative is raised.
The other options are incorrect because:
- Option 'A' states that the degree is the highest of the orders of the differential coefficients occurring in the equation, which is not true. The degree only considers the highest power of the highest order derivative.
- Option 'C' states that any power of the highest order differential coefficient can determine the degree, which is not correct. The degree is defined by the highest power.
- Option 'D' states that the degree is the highest power among the powers of the differential coefficients occurring in the equation, which is inaccurate. The degree only considers the highest power of the highest order derivative.
Therefore, the correct answer is option 'B' as it accurately defines the degree of a differential equation.
The degree of a differential equation is a measure of the highest power of the highest order derivative that appears in the equation. It helps us classify the type of differential equation and determine the appropriate methods for solving it.
Degree of a differential equation:
The degree of a differential equation is determined by the highest power of the highest order derivative present in the equation. In other words, it is the power to which the highest order derivative is raised.
Let's consider an example to understand this concept better:
Example:
Consider the following differential equation:
dy/dx + 3y^2 + 2x = 0
In this equation, the highest order derivative is dy/dx, and it is raised to the power of 1. Therefore, the degree of this differential equation is 1.
Another example:
Example:
Consider the following differential equation:
d^3y/dx^3 + 5(dy/dx)^2 + 2x = 0
In this equation, the highest order derivative is d^3y/dx^3, and it is raised to the power of 1. Therefore, the degree of this differential equation is 1.
Why is the answer option 'B'?
In the given options, option 'B' correctly defines the degree of a differential equation as the highest power of the highest order differential coefficient occurring in it. It aligns with the concept discussed above, where the degree is determined by the highest power to which the highest order derivative is raised.
The other options are incorrect because:
- Option 'A' states that the degree is the highest of the orders of the differential coefficients occurring in the equation, which is not true. The degree only considers the highest power of the highest order derivative.
- Option 'C' states that any power of the highest order differential coefficient can determine the degree, which is not correct. The degree is defined by the highest power.
- Option 'D' states that the degree is the highest power among the powers of the differential coefficients occurring in the equation, which is inaccurate. The degree only considers the highest power of the highest order derivative.
Therefore, the correct answer is option 'B' as it accurately defines the degree of a differential equation.
Free Test
FREE
| Start Free Test |
Community Answer
The degree of a differential equation is defined as thea)Highest of th...
Definition : The degree of a differential equation is defined as the highest power of the highest order derivative involved in the differential, where the equation has been made rational and integral as far as the derivatives are concerned.
degree of DE (1) = 2
degree of DE (2) = 1
degree of DE (3) = 1
An Important Example : Find the degree of the differential equation.
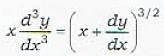
In order to rationalize this equation, we first square this equation and get

Now clearly the degree of the differential equation is 2.
Thus statement (b) gives the correct definition of the degee of a differential equation.
degree of DE (1) = 2
degree of DE (2) = 1
degree of DE (3) = 1
An Important Example : Find the degree of the differential equation.
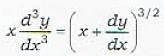
In order to rationalize this equation, we first square this equation and get

Now clearly the degree of the differential equation is 2.
Thus statement (b) gives the correct definition of the degee of a differential equation.

|
Explore Courses for Mathematics exam
|

|
Similar Mathematics Doubts
The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer?
Question Description
The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer?.
The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer?.
Solutions for The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mathematics.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Here you can find the meaning of The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The degree of a differential equation is defined as thea)Highest of the orders of the differential coefficients occuring in itb)Highest power of the highest order differential coefficient occurring in itc)Any power of the highest order differential coefficient occurring in itd)Highest power among the powers of the dif ferential coefficients occurring in itCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Mathematics tests.

|
Explore Courses for Mathematics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















