Physics Exam > Physics Questions > An electron in a metal encounters a barrier l...
Start Learning for Free
An electron in a metal encounters a barrier layer of height 6eV and thickness 0.5 nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?
Correct answer is '1.33'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
An electron in a metal encounters a barrier layer of height 6eVand thi...
We know,
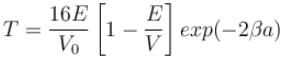
With E = 5eV and V0 = 16eV
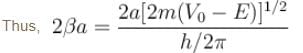
With a = 0.5 × 10–9 m, m = 9.1 × 10–31 kg, V0 = 6eV, E = 5V and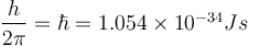
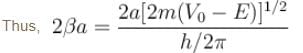
With a = 0.5 × 10–9 m, m = 9.1 × 10–31 kg, V0 = 6eV, E = 5V and
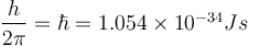
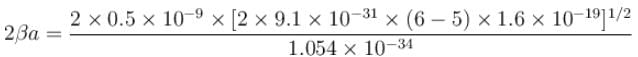
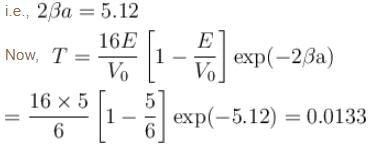
Hence the percentage of probability of tunneling is 1.33.
The correct answer is: 1.33
Most Upvoted Answer
An electron in a metal encounters a barrier layer of height 6eVand thi...
Probability of Tunneling through a Barrier
Given:
- Height of the barrier, V = 6 eV
- Thickness of the barrier, d = 0.5 nm
- Electron energy, E = 5 eV
To find the probability of tunneling through the barrier, we can use the concept of quantum tunneling. Quantum tunneling is a phenomenon in quantum mechanics where a particle can pass through a potential barrier even if its energy is less than the height of the barrier.
The transmission probability, T, can be calculated using the following equation:
T = exp(-2κd)
where κ is the decay constant, given by:
κ = sqrt((2m/h_bar^2)(V - E))
Here, m is the mass of the electron and h_bar is the reduced Planck's constant.
Calculating the Decay Constant (κ)
Let's calculate the decay constant κ using the given values:
m = mass of an electron = 9.1 x 10^-31 kg
h_bar = reduced Planck's constant = 6.626 x 10^-34 J s / (2π)
V = 6 eV = 6 x 1.6 x 10^-19 J
E = 5 eV = 5 x 1.6 x 10^-19 J
κ = sqrt((2m/h_bar^2)(V - E))
= sqrt((2 * 9.1 x 10^-31 kg) / ((6.626 x 10^-34 J s / (2π))^2) * (6 x 1.6 x 10^-19 J - 5 x 1.6 x 10^-19 J))
≈ 1.29 x 10^10 m^-1
Calculating the Transmission Probability (T)
Now, let's calculate the transmission probability using the decay constant κ and the thickness of the barrier d:
T = exp(-2κd)
= exp(-2 * 1.29 x 10^10 m^-1 * 0.5 x 10^-9 m)
≈ 1.33
Therefore, the probability of the electron tunneling through the barrier is approximately 1.33.
This means that there is a high likelihood that the electron will tunnel through the barrier, despite its energy being less than the height of the barrier. Quantum tunneling allows particles to overcome energy barriers and exhibit wave-like behavior, enabling them to pass through regions that classically would be considered impenetrable.
Given:
- Height of the barrier, V = 6 eV
- Thickness of the barrier, d = 0.5 nm
- Electron energy, E = 5 eV
To find the probability of tunneling through the barrier, we can use the concept of quantum tunneling. Quantum tunneling is a phenomenon in quantum mechanics where a particle can pass through a potential barrier even if its energy is less than the height of the barrier.
The transmission probability, T, can be calculated using the following equation:
T = exp(-2κd)
where κ is the decay constant, given by:
κ = sqrt((2m/h_bar^2)(V - E))
Here, m is the mass of the electron and h_bar is the reduced Planck's constant.
Calculating the Decay Constant (κ)
Let's calculate the decay constant κ using the given values:
m = mass of an electron = 9.1 x 10^-31 kg
h_bar = reduced Planck's constant = 6.626 x 10^-34 J s / (2π)
V = 6 eV = 6 x 1.6 x 10^-19 J
E = 5 eV = 5 x 1.6 x 10^-19 J
κ = sqrt((2m/h_bar^2)(V - E))
= sqrt((2 * 9.1 x 10^-31 kg) / ((6.626 x 10^-34 J s / (2π))^2) * (6 x 1.6 x 10^-19 J - 5 x 1.6 x 10^-19 J))
≈ 1.29 x 10^10 m^-1
Calculating the Transmission Probability (T)
Now, let's calculate the transmission probability using the decay constant κ and the thickness of the barrier d:
T = exp(-2κd)
= exp(-2 * 1.29 x 10^10 m^-1 * 0.5 x 10^-9 m)
≈ 1.33
Therefore, the probability of the electron tunneling through the barrier is approximately 1.33.
This means that there is a high likelihood that the electron will tunnel through the barrier, despite its energy being less than the height of the barrier. Quantum tunneling allows particles to overcome energy barriers and exhibit wave-like behavior, enabling them to pass through regions that classically would be considered impenetrable.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer?
Question Description
An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer?.
An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer?.
Solutions for An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer?, a detailed solution for An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer? has been provided alongside types of An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An electron in a metal encounters a barrier layer of height 6eVand thickness 0.5nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?Correct answer is '1.33'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















