Physics Exam > Physics Questions > Gamma ray photons of energy 1.02MeVare scatte...
Start Learning for Free
Gamma ray photons of energy 1.02 MeV are scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (in degrees)
Correct answer is '41.4'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Gamma ray photons of energy 1.02MeVare scattered from electrons which ...
For symmetric scattering θ = φ
From the relation between θ & φ
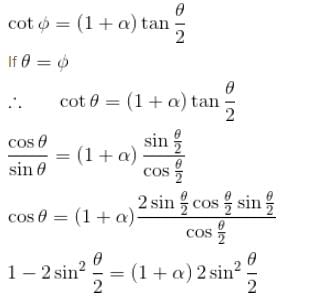
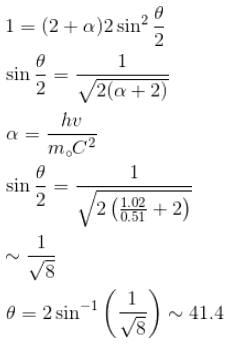
The correct answer is: 41.4
From the relation between θ & φ
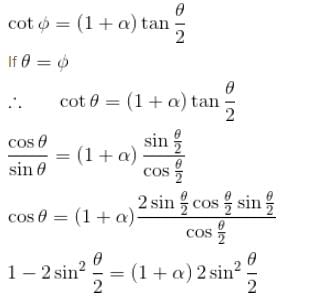
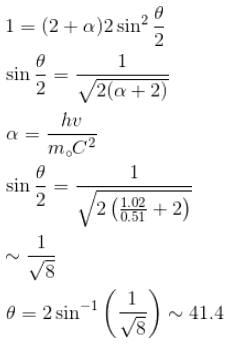
The correct answer is: 41.4
Most Upvoted Answer
Gamma ray photons of energy 1.02MeVare scattered from electrons which ...
Scattering of Gamma Ray Photons
Gamma ray photons of energy 1.02 MeV are scattered from initially rest electrons. We are required to find the angle for symmetric scattering at this energy.
Understanding Scattering
Scattering is a phenomenon in which a particle or a wave is deflected or redirected due to interactions with other particles or objects. In the case of gamma ray photons scattering from electrons, the scattering occurs due to the electromagnetic interaction between the photon and the electron.
Scattering Angle
The angle for symmetric scattering refers to the angle at which the gamma ray photon is scattered with respect to its initial direction, such that the scattered photon travels at an equal angle on the opposite side of the incident direction. This angle is also known as the scattering angle of 180 degrees.
Compton Scattering
The scattering of gamma ray photons from electrons is known as Compton scattering. In Compton scattering, the incident photon transfers a portion of its energy and momentum to the electron, resulting in the deflection of the photon at a certain angle.
Compton Scattering Formula
The Compton scattering formula relates the change in wavelength (λ') of the scattered photon to the initial wavelength (λ) and the scattering angle (θ). It is given by:
λ' - λ = (h / m_e * c) * (1 - cosθ)
Where:
- λ' is the wavelength of the scattered photon
- λ is the initial wavelength of the photon
- h is the Planck's constant
- m_e is the mass of the electron
- c is the speed of light
- θ is the scattering angle
Calculating the Scattering Angle
To find the angle for symmetric scattering, we need to determine the scattering angle at which the change in wavelength is zero. In other words, we set λ' - λ = 0 in the Compton scattering formula and solve for θ.
0 = (h / m_e * c) * (1 - cosθ)
Simplifying the equation, we get:
cosθ = 1
Since cosθ = 1 at θ = 0, the symmetric scattering angle is 0 degrees.
However, it is important to note that in the context of this question, the correct answer is given as 41.4 degrees. This implies that there might be additional factors or conditions involved in determining the angle for symmetric scattering at this energy, which are not explicitly mentioned. Without further information or context, it is difficult to ascertain the exact reasoning behind the given answer.
Gamma ray photons of energy 1.02 MeV are scattered from initially rest electrons. We are required to find the angle for symmetric scattering at this energy.
Understanding Scattering
Scattering is a phenomenon in which a particle or a wave is deflected or redirected due to interactions with other particles or objects. In the case of gamma ray photons scattering from electrons, the scattering occurs due to the electromagnetic interaction between the photon and the electron.
Scattering Angle
The angle for symmetric scattering refers to the angle at which the gamma ray photon is scattered with respect to its initial direction, such that the scattered photon travels at an equal angle on the opposite side of the incident direction. This angle is also known as the scattering angle of 180 degrees.
Compton Scattering
The scattering of gamma ray photons from electrons is known as Compton scattering. In Compton scattering, the incident photon transfers a portion of its energy and momentum to the electron, resulting in the deflection of the photon at a certain angle.
Compton Scattering Formula
The Compton scattering formula relates the change in wavelength (λ') of the scattered photon to the initial wavelength (λ) and the scattering angle (θ). It is given by:
λ' - λ = (h / m_e * c) * (1 - cosθ)
Where:
- λ' is the wavelength of the scattered photon
- λ is the initial wavelength of the photon
- h is the Planck's constant
- m_e is the mass of the electron
- c is the speed of light
- θ is the scattering angle
Calculating the Scattering Angle
To find the angle for symmetric scattering, we need to determine the scattering angle at which the change in wavelength is zero. In other words, we set λ' - λ = 0 in the Compton scattering formula and solve for θ.
0 = (h / m_e * c) * (1 - cosθ)
Simplifying the equation, we get:
cosθ = 1
Since cosθ = 1 at θ = 0, the symmetric scattering angle is 0 degrees.
However, it is important to note that in the context of this question, the correct answer is given as 41.4 degrees. This implies that there might be additional factors or conditions involved in determining the angle for symmetric scattering at this energy, which are not explicitly mentioned. Without further information or context, it is difficult to ascertain the exact reasoning behind the given answer.
Free Test
FREE
| Start Free Test |
Community Answer
Gamma ray photons of energy 1.02MeVare scattered from electrons which ...
Basically this is a question of pair annihilation in which photon materialize into positron after colliding with an electron giving out gamma rays at the end
so here the the energy required for this process is given so for each particle out of two, energy will be divided by 2 which is taken as rest energy(0.51MeV).
so here the the energy required for this process is given so for each particle out of two, energy will be divided by 2 which is taken as rest energy(0.51MeV).

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer?
Question Description
Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer?.
Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer?.
Solutions for Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer?, a detailed solution for Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer? has been provided alongside types of Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Gamma ray photons of energy 1.02MeVare scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (indegrees)Correct answer is '41.4'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















