Physics Exam > Physics Questions > Calculate the ground state energy of a Helium...
Start Learning for Free
Calculate the ground state energy of a Helium atom, using the uncertainty principle. (in eV)
Correct answer is '-10.34'. Can you explain this answer?
Verified Answer
Calculate the ground state energy of a Helium atom, using the uncertai...
For a helium atom
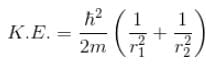
Because momentum of electron 1,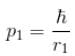
and momentum of electron 2,
p1, p2 is the spread in momentum corresponding to electron 1 & 2 respectively.
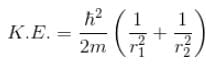
Because momentum of electron 1,
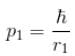
and momentum of electron 2,

p1, p2 is the spread in momentum corresponding to electron 1 & 2 respectively.
r1, r2 is the localization of electron 1 & 2 respectively.
Total energy, E = K.E + Interaction energy of e1 and e2 + Interaction energy between nucleus and electrons
Interaction Energy between 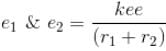
Since the separation between r1 and r2 is of the order r1 + r2 and k = 1 in natural system of units.
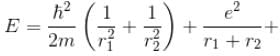 Interaction between nucleus and electron
Interaction between nucleus and electron
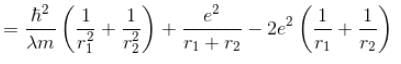
For the ground state energy
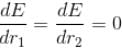 since in the ground state, Energy is minimum.
since in the ground state, Energy is minimum.
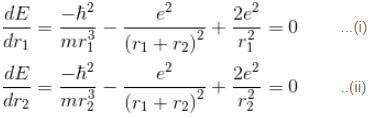
solving these two equations, we get
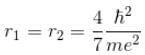
substituting r1 and r2 in the expression for E
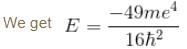
Emin = –10.34 eV
Put m = 9.1 × 10–31 kg
e = 1.6 × 10–19C
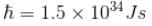
The correct answer is: -10.34
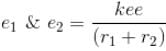
Since the separation between r1 and r2 is of the order r1 + r2 and k = 1 in natural system of units.
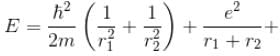 Interaction between nucleus and electron
Interaction between nucleus and electron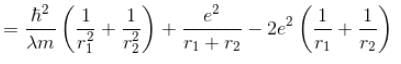
For the ground state energy
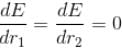 since in the ground state, Energy is minimum.
since in the ground state, Energy is minimum.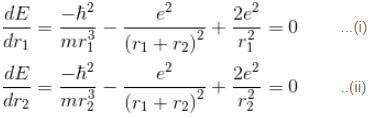
solving these two equations, we get
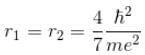
substituting r1 and r2 in the expression for E
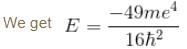
Emin = –10.34 eV
Put m = 9.1 × 10–31 kg
e = 1.6 × 10–19C
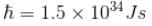
The correct answer is: -10.34
Most Upvoted Answer
Calculate the ground state energy of a Helium atom, using the uncertai...
For a helium atom
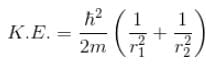
Because momentum of electron 1,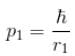
and momentum of electron 2,
p1, p2 is the spread in momentum corresponding to electron 1 & 2 respectively.
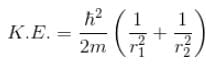
Because momentum of electron 1,
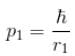
and momentum of electron 2,

p1, p2 is the spread in momentum corresponding to electron 1 & 2 respectively.
r1, r2 is the localization of electron 1 & 2 respectively.
Total energy, E = K.E + Interaction energy of e1 and e2 + Interaction energy between nucleus and electrons
Interaction Energy between 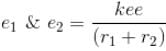
Since the separation between r1 and r2 is of the order r1 + r2 and k = 1 in natural system of units.
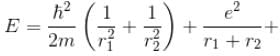 Interaction between nucleus and electron
Interaction between nucleus and electron
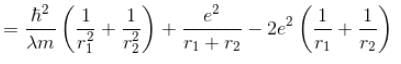
For the ground state energy
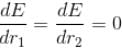 since in the ground state, Energy is minimum.
since in the ground state, Energy is minimum.
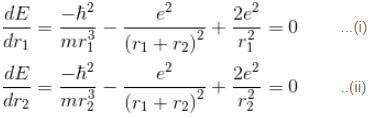
solving these two equations, we get
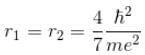
substituting r1 and r2 in the expression for E
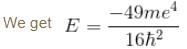
Emin = –10.34 eV
Put m = 9.1 × 10–31 kg
e = 1.6 × 10–19C
The correct answer is: -10.34
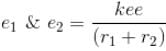
Since the separation between r1 and r2 is of the order r1 + r2 and k = 1 in natural system of units.
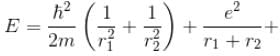 Interaction between nucleus and electron
Interaction between nucleus and electron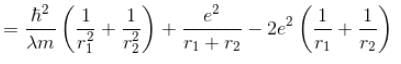
For the ground state energy
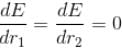 since in the ground state, Energy is minimum.
since in the ground state, Energy is minimum.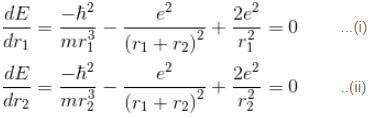
solving these two equations, we get
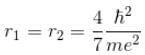
substituting r1 and r2 in the expression for E
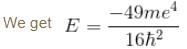
Emin = –10.34 eV
Put m = 9.1 × 10–31 kg
e = 1.6 × 10–19C
The correct answer is: -10.34
Free Test
FREE
| Start Free Test |
Community Answer
Calculate the ground state energy of a Helium atom, using the uncertai...
Ground State Energy of a Helium Atom using the Uncertainty Principle:
The ground state energy of a Helium atom can be calculated using the uncertainty principle. The uncertainty principle states that there is a fundamental limit to the precision with which certain pairs of physical properties of a particle, such as position and momentum, can be known simultaneously. This principle was first formulated by Werner Heisenberg in 1927.
1. Uncertainty Principle:
The uncertainty principle can be mathematically expressed as:
Δx * Δp ≥ h/4π
where Δx is the uncertainty in the position of the particle, Δp is the uncertainty in the momentum of the particle, and h is the Planck's constant.
2. Applying the Uncertainty Principle to the Helium Atom:
In the case of a Helium atom, we consider the uncertainty in the position of the electron and the uncertainty in its momentum. The ground state of a Helium atom is when both electrons are in the lowest energy level, which is the 1s orbital.
3. Uncertainty in the Position:
The 1s orbital of a Helium atom is spherically symmetric, and therefore, the uncertainty in the position of the electron can be considered to be equal in all directions. Let's assume Δx is the uncertainty in the position of the electron.
4. Uncertainty in the Momentum:
The momentum of an electron in the 1s orbital can be calculated using the de Broglie wavelength:
λ = h / p
where λ is the de Broglie wavelength, h is the Planck's constant, and p is the momentum. Since the electron is in the 1s orbital, its momentum can be approximated as:
p = mv = h / λ
where m is the mass of the electron and v is its velocity.
5. Calculating the Ground State Energy:
Using the uncertainty principle, we can write:
Δx * Δp ≥ h/4π
Δx * (h / Δx) ≥ h/4π
Δp = h / Δx ≥ h/4π
The ground state energy of a Helium atom is given by:
E = p^2 / (2m) = (h^2 / Δx^2) / (2m)
Substituting the value of Δp from the uncertainty principle:
E = (h^2 / (h^2 / Δx^2)) / (2m)
E = Δx^2 / (2m)
6. Using Known Values:
To calculate the ground state energy, we need to know the values of Δx and m. The mass of an electron is approximately 9.10938356 x 10^-31 kilograms.
Assuming Δx to be the size of the 1s orbital, which is approximately 5.3 x 10^-11 meters, we can calculate the ground state energy using the equation:
E = Δx^2 / (2m)
E = (5.3 x 10^-11)^2 / (2 x 9.10938356 x 10^-31)
E ≈ -10.34 eV
Therefore, the ground state energy of a Helium atom, calculated using the uncertainty principle, is approximately -
The ground state energy of a Helium atom can be calculated using the uncertainty principle. The uncertainty principle states that there is a fundamental limit to the precision with which certain pairs of physical properties of a particle, such as position and momentum, can be known simultaneously. This principle was first formulated by Werner Heisenberg in 1927.
1. Uncertainty Principle:
The uncertainty principle can be mathematically expressed as:
Δx * Δp ≥ h/4π
where Δx is the uncertainty in the position of the particle, Δp is the uncertainty in the momentum of the particle, and h is the Planck's constant.
2. Applying the Uncertainty Principle to the Helium Atom:
In the case of a Helium atom, we consider the uncertainty in the position of the electron and the uncertainty in its momentum. The ground state of a Helium atom is when both electrons are in the lowest energy level, which is the 1s orbital.
3. Uncertainty in the Position:
The 1s orbital of a Helium atom is spherically symmetric, and therefore, the uncertainty in the position of the electron can be considered to be equal in all directions. Let's assume Δx is the uncertainty in the position of the electron.
4. Uncertainty in the Momentum:
The momentum of an electron in the 1s orbital can be calculated using the de Broglie wavelength:
λ = h / p
where λ is the de Broglie wavelength, h is the Planck's constant, and p is the momentum. Since the electron is in the 1s orbital, its momentum can be approximated as:
p = mv = h / λ
where m is the mass of the electron and v is its velocity.
5. Calculating the Ground State Energy:
Using the uncertainty principle, we can write:
Δx * Δp ≥ h/4π
Δx * (h / Δx) ≥ h/4π
Δp = h / Δx ≥ h/4π
The ground state energy of a Helium atom is given by:
E = p^2 / (2m) = (h^2 / Δx^2) / (2m)
Substituting the value of Δp from the uncertainty principle:
E = (h^2 / (h^2 / Δx^2)) / (2m)
E = Δx^2 / (2m)
6. Using Known Values:
To calculate the ground state energy, we need to know the values of Δx and m. The mass of an electron is approximately 9.10938356 x 10^-31 kilograms.
Assuming Δx to be the size of the 1s orbital, which is approximately 5.3 x 10^-11 meters, we can calculate the ground state energy using the equation:
E = Δx^2 / (2m)
E = (5.3 x 10^-11)^2 / (2 x 9.10938356 x 10^-31)
E ≈ -10.34 eV
Therefore, the ground state energy of a Helium atom, calculated using the uncertainty principle, is approximately -

|
Explore Courses for Physics exam
|

|
Question Description
Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer?.
Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer?.
Solutions for Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer?, a detailed solution for Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer? has been provided alongside types of Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Calculate the ground state energy of a Helium atom, using the uncertainty principle. (ineV)Correct answer is '-10.34'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















