Physics Exam > Physics Questions > A man stands on a weighing machine placed on ...
Start Learning for Free
A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2
- a)Between 1 0 .5 kg force and 90 .5 kg force
- b)Between 9 .5 kg force and 90 .5 kg force
- c)Between 8 .9 kg force and 89 .5 kg force
- d)Between 10.5 kg force and 89 .5 kg force
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A man stands on a weighing machine placed on a horizontal platform. Th...
Here, m = 50kg, v = 2s-1
a = 5 cm = 0.05m
Max. acceleration, amax = ω2a
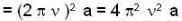
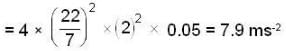
∴ Max. force on the man
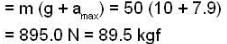
Mini. force on the man
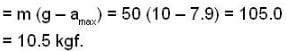
a = 5 cm = 0.05m
Max. acceleration, amax = ω2a
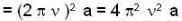
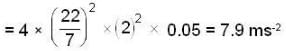
∴ Max. force on the man
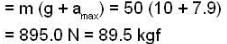
Mini. force on the man
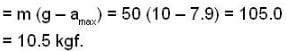
Most Upvoted Answer
A man stands on a weighing machine placed on a horizontal platform. Th...
Effect of Harmonic Vibrations on the Reading of the Weighing Machine
The effect of harmonic vibrations on the reading of the weighing machine can be analyzed by considering the forces acting on the man and the platform during the vibrations.
1. Forces acting on the man:
The man experiences two types of forces while standing on the weighing machine:
- Gravitational force (mg): This force always acts vertically downwards and is constant.
- Normal force (N): This force is exerted by the weighing machine to balance the gravitational force and prevent the man from sinking into the machine. It is equal in magnitude and opposite in direction to the gravitational force.
2. Forces acting on the platform:
The platform undergoes harmonic vibrations with a frequency of 2 vibrations per second and an amplitude of 5 cm. As a result, the platform experiences an oscillating vertical displacement.
- Spring force (Fs): The spring force acts in the opposite direction to the displacement of the platform. It is given by Hooke's Law: Fs = -kx, where k is the spring constant and x is the displacement of the platform from its equilibrium position. The spring force varies sinusoidally with time as the platform oscillates.
- Inertia force (Fi): The inertia force acts in the same direction as the displacement of the platform and is given by Fi = mω²x, where m is the mass of the platform and ω is the angular frequency of oscillation (2πf).
3. Effect on the reading of the weighing machine:
The reading on the weighing machine is determined by the balance between the gravitational force and the normal force. As the platform oscillates, the normal force will vary due to the forces acting on the platform. This will result in a variation in the reading of the weighing machine.
- When the platform is at its extreme positions, the spring force is maximum and the inertia force is minimum. At these positions, the normal force will be greater than the gravitational force, leading to an increase in the reading of the weighing machine.
- When the platform is at its equilibrium position, the spring force and the inertia force are zero. At this position, the normal force will be equal to the gravitational force, resulting in the correct reading of the weighing machine.
- When the platform is at the mid-positions between the extreme positions, the spring force and the inertia force are both present but in opposite directions. The normal force will be less than the gravitational force, leading to a decrease in the reading of the weighing machine.
Considering the given options, it can be concluded that the effect on the reading of the weighing machine will be between 10.5 kg force and 89.5 kg force.
The effect of harmonic vibrations on the reading of the weighing machine can be analyzed by considering the forces acting on the man and the platform during the vibrations.
1. Forces acting on the man:
The man experiences two types of forces while standing on the weighing machine:
- Gravitational force (mg): This force always acts vertically downwards and is constant.
- Normal force (N): This force is exerted by the weighing machine to balance the gravitational force and prevent the man from sinking into the machine. It is equal in magnitude and opposite in direction to the gravitational force.
2. Forces acting on the platform:
The platform undergoes harmonic vibrations with a frequency of 2 vibrations per second and an amplitude of 5 cm. As a result, the platform experiences an oscillating vertical displacement.
- Spring force (Fs): The spring force acts in the opposite direction to the displacement of the platform. It is given by Hooke's Law: Fs = -kx, where k is the spring constant and x is the displacement of the platform from its equilibrium position. The spring force varies sinusoidally with time as the platform oscillates.
- Inertia force (Fi): The inertia force acts in the same direction as the displacement of the platform and is given by Fi = mω²x, where m is the mass of the platform and ω is the angular frequency of oscillation (2πf).
3. Effect on the reading of the weighing machine:
The reading on the weighing machine is determined by the balance between the gravitational force and the normal force. As the platform oscillates, the normal force will vary due to the forces acting on the platform. This will result in a variation in the reading of the weighing machine.
- When the platform is at its extreme positions, the spring force is maximum and the inertia force is minimum. At these positions, the normal force will be greater than the gravitational force, leading to an increase in the reading of the weighing machine.
- When the platform is at its equilibrium position, the spring force and the inertia force are zero. At this position, the normal force will be equal to the gravitational force, resulting in the correct reading of the weighing machine.
- When the platform is at the mid-positions between the extreme positions, the spring force and the inertia force are both present but in opposite directions. The normal force will be less than the gravitational force, leading to a decrease in the reading of the weighing machine.
Considering the given options, it can be concluded that the effect on the reading of the weighing machine will be between 10.5 kg force and 89.5 kg force.
Free Test
FREE
| Start Free Test |
Community Answer
A man stands on a weighing machine placed on a horizontal platform. Th...
Here, m = 50kg, v = 2s-1
a = 5 cm = 0.05m
Max. acceleration, amax = ω2a

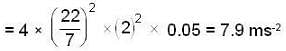
∴ Max. force on the man
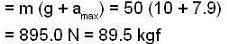
Mini. force on the man
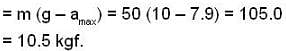
a = 5 cm = 0.05m
Max. acceleration, amax = ω2a

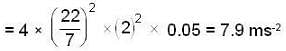
∴ Max. force on the man
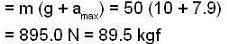
Mini. force on the man
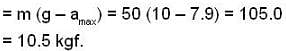

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer?
Question Description
A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer?.
A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer?.
Solutions for A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2a)Between 1 0 .5 kg force and 90 .5 kg forceb)Between 9 .5 kg force and 90 .5 kg forcec)Between 8 .9 kg force and 89 .5 kg forced)Between 10.5 kg force and 89 .5 kg forceCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















