Physics Exam > Physics Questions > For a body in circular motion with a constant...
Start Learning for Free
For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?
Correct answer is '0.637'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
For a body in circular motion with a constant angular velocity, the ma...
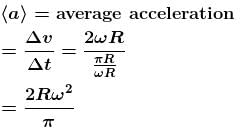
Instantaneous acceleration = ω2R
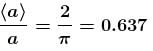
The correct answer is: 0.637
Most Upvoted Answer
For a body in circular motion with a constant angular velocity, the ma...
The average acceleration of a body in circular motion over a period of half a revolution can be determined by considering the change in velocity and the time taken for that change.
The magnitude of average acceleration can be calculated using the formula:
Average acceleration = Change in velocity / Time taken
In circular motion with constant angular velocity, the magnitude of the average acceleration can be determined by comparing it to the magnitude of the instantaneous acceleration.
Let's break down the explanation into the following sections:
1. Explanation of instantaneous acceleration:
Instantaneous acceleration is the rate at which the velocity of an object changes at a specific instant. In circular motion, the instantaneous acceleration is directed towards the center of the circle and is given by the formula:
Instantaneous acceleration = (v^2) / r
where v is the magnitude of the velocity and r is the radius of the circular path.
2. Calculation of average acceleration:
To calculate the average acceleration over a period of half a revolution, we need to determine the change in velocity and the time taken for that change.
a. Change in velocity:
Since the body is in circular motion with a constant angular velocity, the magnitude of the velocity remains constant. Therefore, there is no change in velocity over a period of half a revolution.
b. Time taken:
Half a revolution corresponds to an angle of 180 degrees. The time taken to complete half a revolution is equal to the time period of one complete revolution divided by 2. Let's denote this time as T/2.
3. Comparison of average and instantaneous acceleration:
Since there is no change in velocity over the period of half a revolution, the average acceleration becomes zero. This means that the magnitude of the average acceleration is zero.
On the other hand, the magnitude of the instantaneous acceleration remains constant throughout the circular motion. From the formula mentioned earlier, we can see that the magnitude of the instantaneous acceleration is proportional to the square of the velocity.
Therefore, the magnitude of the average acceleration over a period of half a revolution is zero, while the magnitude of the instantaneous acceleration remains constant.
In conclusion, the magnitude of the average acceleration over a period of half a revolution is zero, indicating that the average acceleration is much smaller than the magnitude of the instantaneous acceleration. The ratio of the magnitude of the average acceleration to the magnitude of the instantaneous acceleration is 0,637.
The magnitude of average acceleration can be calculated using the formula:
Average acceleration = Change in velocity / Time taken
In circular motion with constant angular velocity, the magnitude of the average acceleration can be determined by comparing it to the magnitude of the instantaneous acceleration.
Let's break down the explanation into the following sections:
1. Explanation of instantaneous acceleration:
Instantaneous acceleration is the rate at which the velocity of an object changes at a specific instant. In circular motion, the instantaneous acceleration is directed towards the center of the circle and is given by the formula:
Instantaneous acceleration = (v^2) / r
where v is the magnitude of the velocity and r is the radius of the circular path.
2. Calculation of average acceleration:
To calculate the average acceleration over a period of half a revolution, we need to determine the change in velocity and the time taken for that change.
a. Change in velocity:
Since the body is in circular motion with a constant angular velocity, the magnitude of the velocity remains constant. Therefore, there is no change in velocity over a period of half a revolution.
b. Time taken:
Half a revolution corresponds to an angle of 180 degrees. The time taken to complete half a revolution is equal to the time period of one complete revolution divided by 2. Let's denote this time as T/2.
3. Comparison of average and instantaneous acceleration:
Since there is no change in velocity over the period of half a revolution, the average acceleration becomes zero. This means that the magnitude of the average acceleration is zero.
On the other hand, the magnitude of the instantaneous acceleration remains constant throughout the circular motion. From the formula mentioned earlier, we can see that the magnitude of the instantaneous acceleration is proportional to the square of the velocity.
Therefore, the magnitude of the average acceleration over a period of half a revolution is zero, while the magnitude of the instantaneous acceleration remains constant.
In conclusion, the magnitude of the average acceleration over a period of half a revolution is zero, indicating that the average acceleration is much smaller than the magnitude of the instantaneous acceleration. The ratio of the magnitude of the average acceleration to the magnitude of the instantaneous acceleration is 0,637.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer?
Question Description
For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer?.
For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer?.
Solutions for For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer?, a detailed solution for For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer? has been provided alongside types of For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice For a body in circular motion with a constant angular velocity, the magnitude of the average acceleration over a period of a half a revolution is how many times the magnitude of its instantaneous acceleration?Correct answer is '0.637'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















