Physics Exam > Physics Questions > A particle is projected horizontally from the...
Start Learning for Free
A particle is projected horizontally from the top of a tower with a velocity v0. If v be its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :
- a)v2
- b)1/v
- c)v
- d)v3
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A particle is projected horizontally from the top of a tower with a ve...
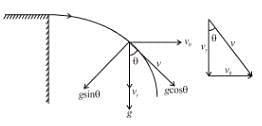
As we know :
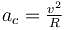 (centripetal acceleration)
(centripetal acceleration)From figure : 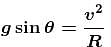
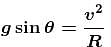
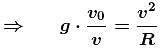


The correct answer is: v3
Most Upvoted Answer
A particle is projected horizontally from the top of a tower with a ve...
The Path of the Projectile
When a particle is projected horizontally from the top of a tower with a velocity v0, it follows a curved path due to the influence of gravity. This path is called the trajectory of the projectile.
The Velocity of the Projectile
The velocity of the projectile can be broken down into two components: the horizontal component (v_x) and the vertical component (v_y). Since the particle is projected horizontally, the initial vertical velocity is zero (v_y0 = 0). The horizontal velocity remains constant throughout the motion, while the vertical velocity changes due to the acceleration of gravity.
At any instant during the projectile's motion, the total velocity (v) can be calculated using the Pythagorean theorem:
v = √(v_x^2 + v_y^2)
The Radius of Curvature
The radius of curvature of the path of the particle at a given instant is a measure of how sharply the trajectory is curved at that point. It is the radius of the circle that best approximates the shape of the curve at that instant.
Proportional Relationship
Now, let's consider the relationship between the radius of curvature and the velocity of the particle. As the velocity of the particle increases, the radius of curvature decreases, indicating a sharper curve. Conversely, as the velocity decreases, the radius of curvature increases, indicating a gentler curve.
Applying the Options
a) v^2: If the radius of curvature is directly proportional to v^2, it means that as the velocity increases, the radius of curvature increases. However, we know that the radius of curvature actually decreases with increasing velocity. Therefore, option 'a' is incorrect.
b) 1/v: If the radius of curvature is directly proportional to 1/v, it means that as the velocity increases, the radius of curvature decreases. This is in line with what we just discussed. Therefore, option 'b' is incorrect.
c) v: If the radius of curvature is directly proportional to v, it means that as the velocity increases, the radius of curvature increases. However, we know that the radius of curvature actually decreases with increasing velocity. Therefore, option 'c' is incorrect.
d) v^3: If the radius of curvature is directly proportional to v^3, it means that as the velocity increases, the radius of curvature decreases. This matches our understanding of the relationship between velocity and the radius of curvature. Therefore, option 'd' is correct.
Conclusion
The correct option is 'd' because the radius of curvature of the path of the projectile at any instant is directly proportional to v^3. As the velocity of the particle increases, the radius of curvature decreases, indicating a sharper curve.
When a particle is projected horizontally from the top of a tower with a velocity v0, it follows a curved path due to the influence of gravity. This path is called the trajectory of the projectile.
The Velocity of the Projectile
The velocity of the projectile can be broken down into two components: the horizontal component (v_x) and the vertical component (v_y). Since the particle is projected horizontally, the initial vertical velocity is zero (v_y0 = 0). The horizontal velocity remains constant throughout the motion, while the vertical velocity changes due to the acceleration of gravity.
At any instant during the projectile's motion, the total velocity (v) can be calculated using the Pythagorean theorem:
v = √(v_x^2 + v_y^2)
The Radius of Curvature
The radius of curvature of the path of the particle at a given instant is a measure of how sharply the trajectory is curved at that point. It is the radius of the circle that best approximates the shape of the curve at that instant.
Proportional Relationship
Now, let's consider the relationship between the radius of curvature and the velocity of the particle. As the velocity of the particle increases, the radius of curvature decreases, indicating a sharper curve. Conversely, as the velocity decreases, the radius of curvature increases, indicating a gentler curve.
Applying the Options
a) v^2: If the radius of curvature is directly proportional to v^2, it means that as the velocity increases, the radius of curvature increases. However, we know that the radius of curvature actually decreases with increasing velocity. Therefore, option 'a' is incorrect.
b) 1/v: If the radius of curvature is directly proportional to 1/v, it means that as the velocity increases, the radius of curvature decreases. This is in line with what we just discussed. Therefore, option 'b' is incorrect.
c) v: If the radius of curvature is directly proportional to v, it means that as the velocity increases, the radius of curvature increases. However, we know that the radius of curvature actually decreases with increasing velocity. Therefore, option 'c' is incorrect.
d) v^3: If the radius of curvature is directly proportional to v^3, it means that as the velocity increases, the radius of curvature decreases. This matches our understanding of the relationship between velocity and the radius of curvature. Therefore, option 'd' is correct.
Conclusion
The correct option is 'd' because the radius of curvature of the path of the projectile at any instant is directly proportional to v^3. As the velocity of the particle increases, the radius of curvature decreases, indicating a sharper curve.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer?
Question Description
A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer?.
A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer?.
Solutions for A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer?, a detailed solution for A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A particle is projected horizontally from the top of a tower with a velocity v0.Ifvbe its velocity at any instant, then from radius of curvature of the path of the particle at that instant is directly proportional to :a)v2b)1/vc)vd)v3Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















