NEET Exam > NEET Questions > An inclined plane sin theta is equals to 7 by...
Start Learning for Free
An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is?
Most Upvoted Answer
An inclined plane sin theta is equals to 7 by 25 a block is placed on ...
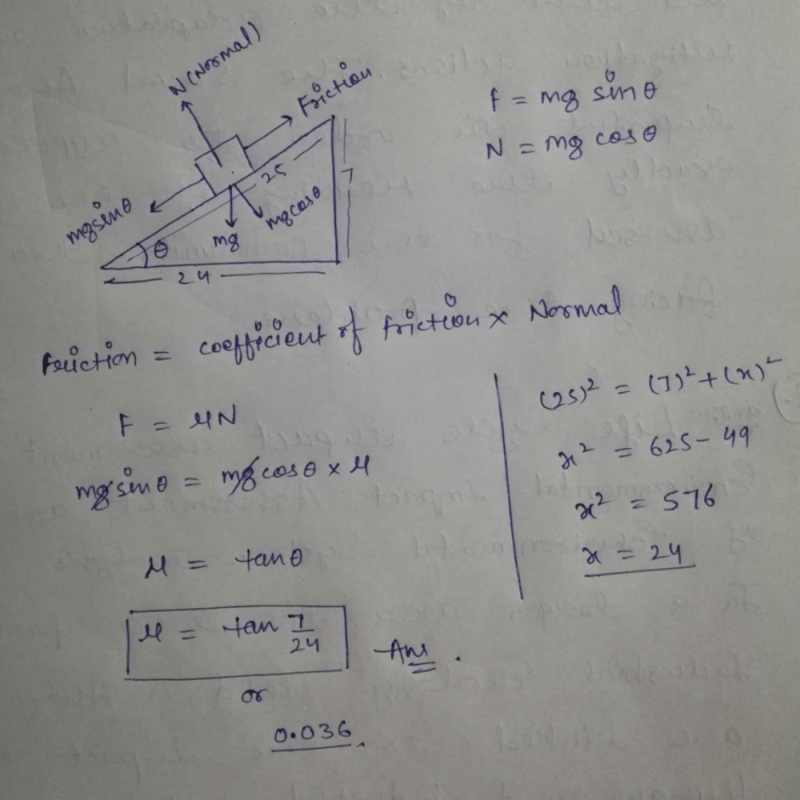
Community Answer
An inclined plane sin theta is equals to 7 by 25 a block is placed on ...
**Inclined Plane and the Block on it**
An inclined plane is a sloping surface that connects a lower point to a higher point. When an object is placed on an inclined plane, it experiences a gravitational force pulling it downwards. This force can be resolved into two components: one parallel to the plane and one perpendicular to the plane.
In this case, the inclined plane is described by the angle theta (θ). The given equation, sin θ = 7/25, tells us the ratio of the length of the side opposite to the angle to the length of the hypotenuse of a right triangle formed by the inclined plane.
**Static Friction and the Block**
Static friction is the force that opposes the motion between two surfaces in contact when there is no relative motion between them. It prevents the block from sliding down the inclined plane until a certain threshold is reached.
When the block is just about to slide down the inclined plane, the force of static friction is at its maximum value. We can denote this force as F_static_max.
**Calculating the Coefficient of Static Friction**
The coefficient of static friction (μ_static) is a dimensionless constant that represents the frictional force between two surfaces in contact. It is given by the equation:
μ_static = F_static_max / N
where N is the normal force exerted by the block on the inclined plane. The normal force is equal to the component of the weight of the block perpendicular to the inclined plane, which is given by:
N = mg cos θ
where m is the mass of the block and g is the acceleration due to gravity.
**Substituting Values and Calculating the Coefficient of Static Friction**
From the given equation sin θ = 7/25, we can find the value of cos θ by using the identity sin² θ + cos² θ = 1:
cos θ = √(1 - sin² θ) = √(1 - (7/25)²) = 24/25
Substituting this value into the equation for N:
N = mg cos θ = mg * (24/25)
Now, substituting the expression for N into the equation for μ_static:
μ_static = F_static_max / N = F_static_max / (mg * (24/25))
Unfortunately, we need more information to calculate the coefficient of static friction. We would require the mass of the block (m) and the acceleration due to gravity (g) to proceed with the calculation.
An inclined plane is a sloping surface that connects a lower point to a higher point. When an object is placed on an inclined plane, it experiences a gravitational force pulling it downwards. This force can be resolved into two components: one parallel to the plane and one perpendicular to the plane.
In this case, the inclined plane is described by the angle theta (θ). The given equation, sin θ = 7/25, tells us the ratio of the length of the side opposite to the angle to the length of the hypotenuse of a right triangle formed by the inclined plane.
**Static Friction and the Block**
Static friction is the force that opposes the motion between two surfaces in contact when there is no relative motion between them. It prevents the block from sliding down the inclined plane until a certain threshold is reached.
When the block is just about to slide down the inclined plane, the force of static friction is at its maximum value. We can denote this force as F_static_max.
**Calculating the Coefficient of Static Friction**
The coefficient of static friction (μ_static) is a dimensionless constant that represents the frictional force between two surfaces in contact. It is given by the equation:
μ_static = F_static_max / N
where N is the normal force exerted by the block on the inclined plane. The normal force is equal to the component of the weight of the block perpendicular to the inclined plane, which is given by:
N = mg cos θ
where m is the mass of the block and g is the acceleration due to gravity.
**Substituting Values and Calculating the Coefficient of Static Friction**
From the given equation sin θ = 7/25, we can find the value of cos θ by using the identity sin² θ + cos² θ = 1:
cos θ = √(1 - sin² θ) = √(1 - (7/25)²) = 24/25
Substituting this value into the equation for N:
N = mg cos θ = mg * (24/25)
Now, substituting the expression for N into the equation for μ_static:
μ_static = F_static_max / N = F_static_max / (mg * (24/25))
Unfortunately, we need more information to calculate the coefficient of static friction. We would require the mass of the block (m) and the acceleration due to gravity (g) to proceed with the calculation.

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is?
Question Description
An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is?.
An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is?.
Solutions for An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is? defined & explained in the simplest way possible. Besides giving the explanation of
An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is?, a detailed solution for An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is? has been provided alongside types of An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is? theory, EduRev gives you an
ample number of questions to practice An inclined plane sin theta is equals to 7 by 25 a block is placed on it just about to slide down the coefficient of static friction between the block and the inclined plane is? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



























