Class 10 Exam > Class 10 Questions > pythagoras theotem Related: Pythagoras Theor...
Start Learning for Free
pythagoras theotem
? Related: Pythagoras Theorem
Most Upvoted Answer
pythagoras theotem Related: Pythagoras Theorem?
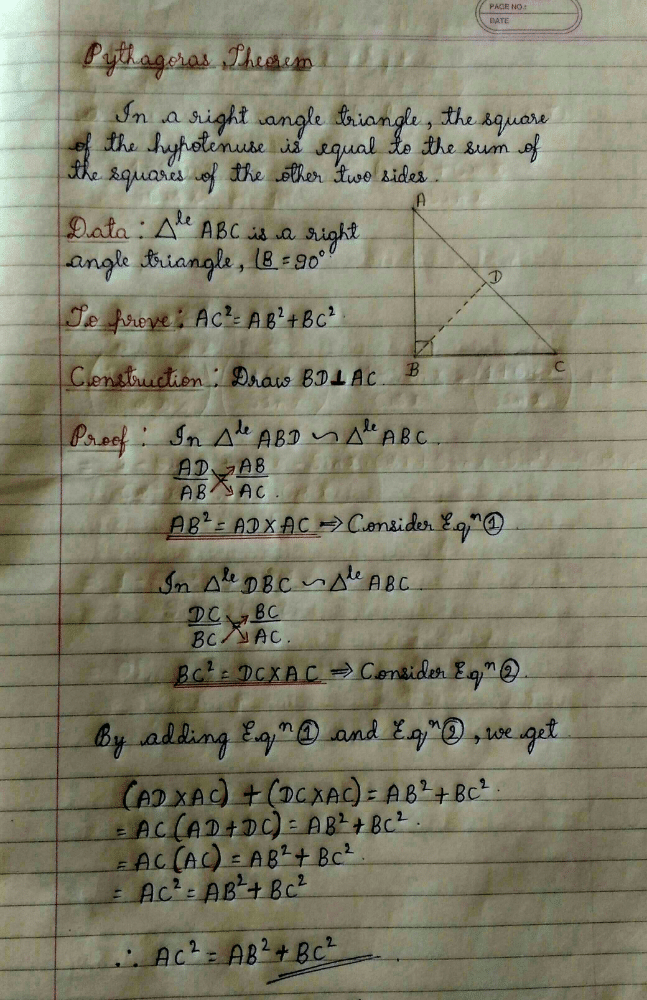
Community Answer
pythagoras theotem Related: Pythagoras Theorem?
**Pythagoras Theorem**
**Introduction:**
Pythagoras Theorem is a fundamental concept in mathematics that relates to the sides of a right-angled triangle. It is named after the ancient Greek mathematician Pythagoras, who is credited with its discovery. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
**The Theorem:**
The Pythagorean Theorem can be stated mathematically as:
c² = a² + b²
where c represents the length of the hypotenuse, and a and b represent the lengths of the other two sides of the right-angled triangle.
**Proof of the Theorem:**
There are various mathematical proofs to establish the validity of the Pythagorean Theorem. One of the most common proofs is the geometric proof, which involves using squares to demonstrate the relationship between the sides of a right-angled triangle.
**Geometric Proof:**
1. Start with a right-angled triangle ABC, where angle C is the right angle.
2. Construct squares on each side of the triangle, forming squares ABDE, BCFG, and ACHI.
3. The area of square ABDE is equal to the sum of the areas of squares BCFG and ACHI.
4. Using the formulas for the areas of squares, we can derive the equation:
(a + b)² = a² + b² + 2ab
5. Simplifying this equation gives:
a² + b² = (a + b)² - 2ab
6. Since the areas of squares ABDE, BCFG, and ACHI are equal, we can equate their respective side lengths:
c² = a² + b²
7. Thus, the Pythagorean Theorem is proven.
**Application of the Theorem:**
The Pythagorean Theorem has numerous applications in mathematics, physics, engineering, and everyday life. Some common applications include:
- Calculating the distance between two points in a coordinate plane.
- Determining the length of a diagonal or a side of a rectangle.
- Solving problems involving right-angled triangles, such as finding missing sides or angles.
- Applying trigonometry to solve real-world problems, such as measuring distances or heights using angles and distances.
In conclusion, the Pythagorean Theorem is a fundamental concept in mathematics that relates to the sides of a right-angled triangle. It has a wide range of applications and is proven through various mathematical proofs, including the geometric proof. Understanding and applying this theorem is crucial in many fields of study and everyday situations.
**Introduction:**
Pythagoras Theorem is a fundamental concept in mathematics that relates to the sides of a right-angled triangle. It is named after the ancient Greek mathematician Pythagoras, who is credited with its discovery. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
**The Theorem:**
The Pythagorean Theorem can be stated mathematically as:
c² = a² + b²
where c represents the length of the hypotenuse, and a and b represent the lengths of the other two sides of the right-angled triangle.
**Proof of the Theorem:**
There are various mathematical proofs to establish the validity of the Pythagorean Theorem. One of the most common proofs is the geometric proof, which involves using squares to demonstrate the relationship between the sides of a right-angled triangle.
**Geometric Proof:**
1. Start with a right-angled triangle ABC, where angle C is the right angle.
2. Construct squares on each side of the triangle, forming squares ABDE, BCFG, and ACHI.
3. The area of square ABDE is equal to the sum of the areas of squares BCFG and ACHI.
4. Using the formulas for the areas of squares, we can derive the equation:
(a + b)² = a² + b² + 2ab
5. Simplifying this equation gives:
a² + b² = (a + b)² - 2ab
6. Since the areas of squares ABDE, BCFG, and ACHI are equal, we can equate their respective side lengths:
c² = a² + b²
7. Thus, the Pythagorean Theorem is proven.
**Application of the Theorem:**
The Pythagorean Theorem has numerous applications in mathematics, physics, engineering, and everyday life. Some common applications include:
- Calculating the distance between two points in a coordinate plane.
- Determining the length of a diagonal or a side of a rectangle.
- Solving problems involving right-angled triangles, such as finding missing sides or angles.
- Applying trigonometry to solve real-world problems, such as measuring distances or heights using angles and distances.
In conclusion, the Pythagorean Theorem is a fundamental concept in mathematics that relates to the sides of a right-angled triangle. It has a wide range of applications and is proven through various mathematical proofs, including the geometric proof. Understanding and applying this theorem is crucial in many fields of study and everyday situations.

|
Explore Courses for Class 10 exam
|

|
Similar Class 10 Doubts
pythagoras theotem Related: Pythagoras Theorem?
Question Description
pythagoras theotem Related: Pythagoras Theorem? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about pythagoras theotem Related: Pythagoras Theorem? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for pythagoras theotem Related: Pythagoras Theorem?.
pythagoras theotem Related: Pythagoras Theorem? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about pythagoras theotem Related: Pythagoras Theorem? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for pythagoras theotem Related: Pythagoras Theorem?.
Solutions for pythagoras theotem Related: Pythagoras Theorem? in English & in Hindi are available as part of our courses for Class 10.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Here you can find the meaning of pythagoras theotem Related: Pythagoras Theorem? defined & explained in the simplest way possible. Besides giving the explanation of
pythagoras theotem Related: Pythagoras Theorem?, a detailed solution for pythagoras theotem Related: Pythagoras Theorem? has been provided alongside types of pythagoras theotem Related: Pythagoras Theorem? theory, EduRev gives you an
ample number of questions to practice pythagoras theotem Related: Pythagoras Theorem? tests, examples and also practice Class 10 tests.

|
Explore Courses for Class 10 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























