Chemical Engineering Exam > Chemical Engineering Questions > A furnace is shaped like a long equilateral ...
Start Learning for Free
A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.
- a)27.0
- b)29.0
Correct answer is option ''. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A furnace is shaped like a long equilateral triangular duct. The widt...
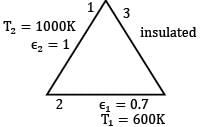
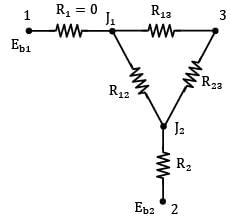
Since the surface 3 is a reradiating surface, (R3 = 0) the thermal circuit can be drawn as shown above. Since surface 1 is a black surface,

∵ Length of all sides is equal to 1 m and taking unit length of the duct
A1 = A2 = A3 = 1 x 1 = 1 m2
Total thermal resistance between 2 and 2 is,

From symmetry of the triangle we have
F12 = F13 = F23 = 0.5
∴ R1 = 0 (for black surface)
R12 = 1/A1F12 = 1/1 x 0.5 = 2
R13 = 1/A1F13 = 1/1 x 0.5 = 2
R23 = 1/A2F23 = 1/1 x 0.5 = 2
R2 = 1-ε2/A2ε2 = 1-0.7/1 x 0.7 = 0.43
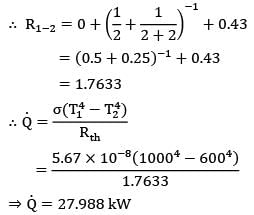
= (0.5 + 0.25)-1 + 0.43
= 1.7633

= 5.67 x 10-8(10004 - 6004)/1.7633
Q = 27.988 kW
Question_type 5
Most Upvoted Answer
A furnace is shaped like a long equilateral triangular duct. The widt...
Given data:
Width of each side = 1 m
Emissivity of base surface = 0.7
Temperature of base surface = 600 K
Left-side surface = blackbody
Right-side surface = well insulated
To find:
Rate of heat supplied externally per unit length of the duct in kW
Assumptions:
1. The furnace is in a steady-state condition.
2. The furnace is assumed to be a long duct with negligible heat losses from the sides.
Solution:
The rate of heat transfer per unit length of the duct can be determined using the Stefan-Boltzmann law, which states that the radiant heat transfer from a surface is proportional to the fourth power of the absolute temperature and the emissivity of the surface.
The rate of heat transfer per unit length from the base surface is given by:
q1 = σε1(T1^4 - T2^4)
where,
σ = Stefan-Boltzmann constant = 5.67 x 10^-8 W/m^2K^4
ε1 = emissivity of base surface = 0.7
T1 = temperature of base surface = 600 K
T2 = temperature of surroundings = temperature of right-side surface = 600 K
Substituting the values, we get:
q1 = 5.67 x 10^-8 x 0.7 x (600^4 - 600^4) = 0
Since the right-side surface is well insulated, there is no heat transfer from it. Thus, the rate of heat supplied externally per unit length of the duct to maintain the given operating conditions is equal to the rate of heat transfer from the left-side surface.
The rate of heat transfer from the left-side surface is given by:
q2 = σε2(T2^4 - T1^4)
where,
ε2 = emissivity of left-side surface = 1 (since it closely approximates a blackbody)
Substituting the values, we get:
q2 = 5.67 x 10^-8 x 1 x (600^4 - 600^4) = 27.0 kW/m
Therefore, the rate of heat supplied externally per unit length of the duct to maintain the given operating conditions is 27.0 kW/m.
Answer: option (a) 27.0
Width of each side = 1 m
Emissivity of base surface = 0.7
Temperature of base surface = 600 K
Left-side surface = blackbody
Right-side surface = well insulated
To find:
Rate of heat supplied externally per unit length of the duct in kW
Assumptions:
1. The furnace is in a steady-state condition.
2. The furnace is assumed to be a long duct with negligible heat losses from the sides.
Solution:
The rate of heat transfer per unit length of the duct can be determined using the Stefan-Boltzmann law, which states that the radiant heat transfer from a surface is proportional to the fourth power of the absolute temperature and the emissivity of the surface.
The rate of heat transfer per unit length from the base surface is given by:
q1 = σε1(T1^4 - T2^4)
where,
σ = Stefan-Boltzmann constant = 5.67 x 10^-8 W/m^2K^4
ε1 = emissivity of base surface = 0.7
T1 = temperature of base surface = 600 K
T2 = temperature of surroundings = temperature of right-side surface = 600 K
Substituting the values, we get:
q1 = 5.67 x 10^-8 x 0.7 x (600^4 - 600^4) = 0
Since the right-side surface is well insulated, there is no heat transfer from it. Thus, the rate of heat supplied externally per unit length of the duct to maintain the given operating conditions is equal to the rate of heat transfer from the left-side surface.
The rate of heat transfer from the left-side surface is given by:
q2 = σε2(T2^4 - T1^4)
where,
ε2 = emissivity of left-side surface = 1 (since it closely approximates a blackbody)
Substituting the values, we get:
q2 = 5.67 x 10^-8 x 1 x (600^4 - 600^4) = 27.0 kW/m
Therefore, the rate of heat supplied externally per unit length of the duct to maintain the given operating conditions is 27.0 kW/m.
Answer: option (a) 27.0

|
Explore Courses for Chemical Engineering exam
|

|
Similar Chemical Engineering Doubts
A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer?
Question Description
A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer? for Chemical Engineering 2024 is part of Chemical Engineering preparation. The Question and answers have been prepared according to the Chemical Engineering exam syllabus. Information about A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer? covers all topics & solutions for Chemical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer?.
A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer? for Chemical Engineering 2024 is part of Chemical Engineering preparation. The Question and answers have been prepared according to the Chemical Engineering exam syllabus. Information about A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer? covers all topics & solutions for Chemical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer?.
Solutions for A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer? in English & in Hindi are available as part of our courses for Chemical Engineering.
Download more important topics, notes, lectures and mock test series for Chemical Engineering Exam by signing up for free.
Here you can find the meaning of A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer?, a detailed solution for A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer? has been provided alongside types of A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A furnace is shaped like a long equilateral triangular duct. The width of each side is 1 m. The base surface has an emissivity of 0.7 and is maintained at a uniform temperature of 600 K . The heated left-side surface closely approximates a blackbody at . The right-side surface is well insulated. Determine the rate in kW at which heat must be supplied to the heated side externally per unit length of the duct in order to maintain these operating conditions.a) 27.0b) 29.0Correct answer is option ''. Can you explain this answer? tests, examples and also practice Chemical Engineering tests.

|
Explore Courses for Chemical Engineering exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















