Mechanical Engineering Exam > Mechanical Engineering Questions > The standard deviation of the critical path i...
Start Learning for Free
The standard deviation of the critical path is
[2009]
- a)0.33
- b)0.55
- c)0.88
- d)1.66
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88...
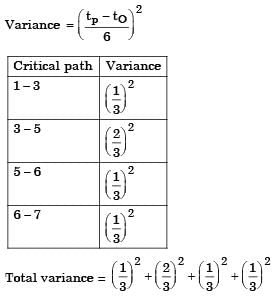
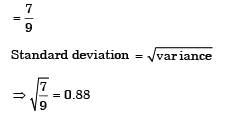
Most Upvoted Answer
The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88...
The standard deviation of the critical path is a measure of the variability or uncertainty in the completion time of the project. It helps in understanding the risks associated with the project schedule and aids in making informed decisions regarding project management. In this case, the correct answer is option 'C' which is 0.88.
Here, we will discuss the concept of critical path, its standard deviation, and how it is calculated.
Critical Path:
The critical path is the longest sequence of dependent activities that determines the total duration of a project. It represents the shortest possible time required to complete the project. Any delay in the activities on the critical path will directly impact the overall project completion time.
Standard Deviation:
The standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of values. It provides insight into the spread of data points around the mean value. In the context of project management, the standard deviation of the critical path helps in estimating the uncertainty or variability in the project completion time.
Calculating the Standard Deviation of the Critical Path:
To calculate the standard deviation of the critical path, we need to determine the duration and standard deviation of each activity on the critical path. The standard deviation of an activity can be obtained using the PERT (Program Evaluation and Review Technique) analysis, which considers optimistic, pessimistic, and most likely time estimates.
The standard deviation of the critical path is the square root of the sum of the variances of individual activities on the critical path. The variance of an activity is calculated as the square of the standard deviation.
Mathematically, the standard deviation of the critical path can be expressed as:
Standard Deviation = √(∑(Variance of activities on the critical path))
In this case, the correct answer is option 'C' which is 0.88. This implies that the sum of the variances of activities on the critical path is 0.88 squared units.
To determine the specific values of variances and calculate the standard deviation, more information about the project and the critical path is required. The given options represent the different values of the standard deviation, and option 'C' is the correct one based on the given information.
Here, we will discuss the concept of critical path, its standard deviation, and how it is calculated.
Critical Path:
The critical path is the longest sequence of dependent activities that determines the total duration of a project. It represents the shortest possible time required to complete the project. Any delay in the activities on the critical path will directly impact the overall project completion time.
Standard Deviation:
The standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of values. It provides insight into the spread of data points around the mean value. In the context of project management, the standard deviation of the critical path helps in estimating the uncertainty or variability in the project completion time.
Calculating the Standard Deviation of the Critical Path:
To calculate the standard deviation of the critical path, we need to determine the duration and standard deviation of each activity on the critical path. The standard deviation of an activity can be obtained using the PERT (Program Evaluation and Review Technique) analysis, which considers optimistic, pessimistic, and most likely time estimates.
The standard deviation of the critical path is the square root of the sum of the variances of individual activities on the critical path. The variance of an activity is calculated as the square of the standard deviation.
Mathematically, the standard deviation of the critical path can be expressed as:
Standard Deviation = √(∑(Variance of activities on the critical path))
In this case, the correct answer is option 'C' which is 0.88. This implies that the sum of the variances of activities on the critical path is 0.88 squared units.
To determine the specific values of variances and calculate the standard deviation, more information about the project and the critical path is required. The given options represent the different values of the standard deviation, and option 'C' is the correct one based on the given information.
Attention Mechanical Engineering Students!
To make sure you are not studying endlessly, EduRev has designed Mechanical Engineering study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Mechanical Engineering.

|
Explore Courses for Mechanical Engineering exam
|

|
Similar Mechanical Engineering Doubts
The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer?
Question Description
The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer?.
The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer?.
Solutions for The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer?, a detailed solution for The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The standard deviation of the critical path is[2009]a)0.33b)0.55c)0.88d)1.66Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























