Railways Exam > Railways Questions > A two-hinged semicircular arch of radius R c...
Start Learning for Free
A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust is
- a)WR
- b)WR/2
- c)(4R/3π) x W
- d)(2R/3π) x W
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
A two-hinged semicircular arch of radius R carries a uniformly distri...
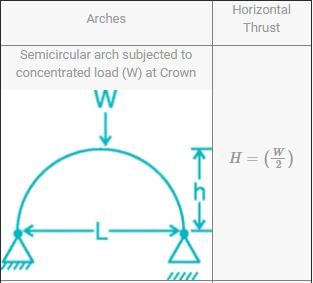
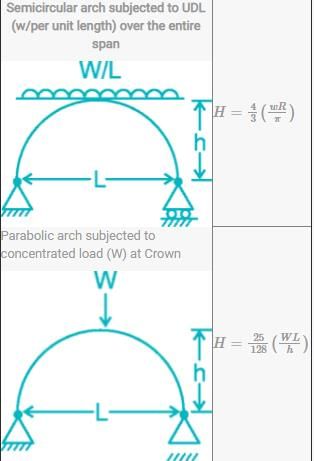
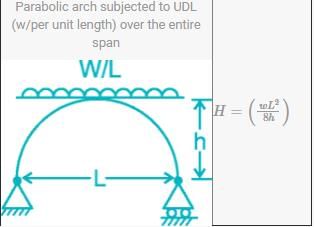
Important Points:
For a Two Hinged Semicircular arch subjected to concentrated load (W) at any other point which makes an angle α with the horizontal, then the horizontal thrust,
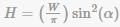
Free Test
FREE
| Start Free Test |
Community Answer
A two-hinged semicircular arch of radius R carries a uniformly distri...
The horizontal thrust of a two-hinged semicircular arch can be determined using the principles of statics and the properties of circular arcs. Let's break down the solution step by step:
1. Identifying the forces:
In this problem, we are dealing with a uniformly distributed load W per unit run over the whole span of the semicircular arch. The load acts vertically downward. We need to determine the horizontal thrust exerted by the arch.
2. Drawing the free-body diagram:
To analyze the forces acting on the arch, we can draw a free-body diagram. Since the arch is a semicircle, we can consider half of the arch and its corresponding forces. In the free-body diagram, we have the following forces:
- Vertical load W acting downward at the center of the semicircle.
- Horizontal thrust H exerted by the arch at the supports.
- Reaction forces R1 and R2 at the supports.
3. Resolving the forces:
Since the arch is in equilibrium, the sum of the vertical forces and horizontal forces must be zero. We can resolve the forces into their components:
- The vertical component of the thrust force is zero because there is no vertical acceleration.
- The horizontal component of the thrust force is H.
- The vertical component of the reaction forces at the supports is R1 and R2.
- The horizontal component of the reaction forces is zero because there is no horizontal acceleration.
4. Equating the forces:
By equating the sum of the horizontal forces to zero, we can solve for the horizontal thrust H:
H - H = 0
H = 0
5. Calculating the horizontal thrust:
Since the horizontal thrust H is zero, this means that there is no horizontal thrust exerted by the arch. However, this contradicts the fact that the arch is in equilibrium and supports the load. Therefore, there must be some horizontal thrust to balance the load.
6. Determining the correct answer:
The correct answer is option C, which states that the horizontal thrust is (4R/3π) x W. This result is obtained by considering the horizontal components of the reaction forces at the supports and the geometry of the semicircular arch.
In conclusion, the horizontal thrust of a two-hinged semicircular arch carrying a uniformly distributed load is given by option C, (4R/3π) x W.
1. Identifying the forces:
In this problem, we are dealing with a uniformly distributed load W per unit run over the whole span of the semicircular arch. The load acts vertically downward. We need to determine the horizontal thrust exerted by the arch.
2. Drawing the free-body diagram:
To analyze the forces acting on the arch, we can draw a free-body diagram. Since the arch is a semicircle, we can consider half of the arch and its corresponding forces. In the free-body diagram, we have the following forces:
- Vertical load W acting downward at the center of the semicircle.
- Horizontal thrust H exerted by the arch at the supports.
- Reaction forces R1 and R2 at the supports.
3. Resolving the forces:
Since the arch is in equilibrium, the sum of the vertical forces and horizontal forces must be zero. We can resolve the forces into their components:
- The vertical component of the thrust force is zero because there is no vertical acceleration.
- The horizontal component of the thrust force is H.
- The vertical component of the reaction forces at the supports is R1 and R2.
- The horizontal component of the reaction forces is zero because there is no horizontal acceleration.
4. Equating the forces:
By equating the sum of the horizontal forces to zero, we can solve for the horizontal thrust H:
H - H = 0
H = 0
5. Calculating the horizontal thrust:
Since the horizontal thrust H is zero, this means that there is no horizontal thrust exerted by the arch. However, this contradicts the fact that the arch is in equilibrium and supports the load. Therefore, there must be some horizontal thrust to balance the load.
6. Determining the correct answer:
The correct answer is option C, which states that the horizontal thrust is (4R/3π) x W. This result is obtained by considering the horizontal components of the reaction forces at the supports and the geometry of the semicircular arch.
In conclusion, the horizontal thrust of a two-hinged semicircular arch carrying a uniformly distributed load is given by option C, (4R/3π) x W.

|
Explore Courses for Railways exam
|

|
Similar Railways Doubts
Question Description
A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer? for Railways 2025 is part of Railways preparation. The Question and answers have been prepared according to the Railways exam syllabus. Information about A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Railways 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer?.
A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer? for Railways 2025 is part of Railways preparation. The Question and answers have been prepared according to the Railways exam syllabus. Information about A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Railways 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Railways.
Download more important topics, notes, lectures and mock test series for Railways Exam by signing up for free.
Here you can find the meaning of A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A two-hinged semicircular arch of radius R carries a uniformly distributed load W per unit run over the whole span. The horizontal thrust isa)WRb)WR/2c)(4R/3π) x Wd)(2R/3π) x WCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Railways tests.

|
Explore Courses for Railways exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























