CAT Exam > CAT Questions > What is the sum of all multiples of 3 less th...
Start Learning for Free
What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?
Correct answer is '75837'. Can you explain this answer?
Most Upvoted Answer
What is the sum of all multiples of 3 less than 1000 which give an odd...
The LCM of 3 and 11 is 33. Thus, the number of numbers we find in the first 33 numbers will be the number of numbers that are there in every consecutive set 33 numbers.
Multiples of 3 less than 33 that have odd remainders when divided by 11 : 3,9,12,18,27
In the next set of 33 numbers, the numbers that satisfy the conditions are : 36,42,45,51,60 ie 33+3,33+9,33+12,33+18,33+27 respectively.
Below 1000, there will be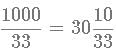
which means there will be 30 such sets.
From 33x30 to 1000, ie from 990 to 1000, there are only 2 more numbers that satisfy the conditions ie 993 and 999.
To find sum of all the numbers, first we find the sum of the first series of numbers ie all numbers below 33 that satisfy the condition.
S1 =3+9+12+18+27=69
The sum of the second series of numbers S2 = (3+33)+(9+33)+(12+33)+(18+33)+(27+33) = 69 + (5 * 33) = 69+165
Similarly, the sum of the third series of numbers S3 =69+(165×2)
Thus, sum of the nth series of numbers Sn =69+[165×(n−1)]
Thus, total sum of the series till the 30th set of numbers S=(69×30)+[165×(1+2+3.....29)]
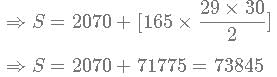
We should remember that this series does not take into consideration the last 2 numbers.
Therefore the actual sum S' = 73845 + 993 + 999 = 75837
Multiples of 3 less than 33 that have odd remainders when divided by 11 : 3,9,12,18,27
In the next set of 33 numbers, the numbers that satisfy the conditions are : 36,42,45,51,60 ie 33+3,33+9,33+12,33+18,33+27 respectively.
Below 1000, there will be
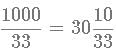which means there will be 30 such sets.From 33x30 to 1000, ie from 990 to 1000, there are only 2 more numbers that satisfy the conditions ie 993 and 999.
To find sum of all the numbers, first we find the sum of the first series of numbers ie all numbers below 33 that satisfy the condition.
S1 =3+9+12+18+27=69
The sum of the second series of numbers S2 = (3+33)+(9+33)+(12+33)+(18+33)+(27+33) = 69 + (5 * 33) = 69+165
Similarly, the sum of the third series of numbers S3 =69+(165×2)
Thus, sum of the nth series of numbers Sn =69+[165×(n−1)]
Thus, total sum of the series till the 30th set of numbers S=(69×30)+[165×(1+2+3.....29)]
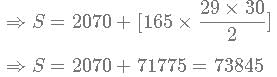
We should remember that this series does not take into consideration the last 2 numbers.
Therefore the actual sum S' = 73845 + 993 + 999 = 75837
Free Test
FREE
| Start Free Test |
Community Answer
What is the sum of all multiples of 3 less than 1000 which give an odd...
**Explanation:**
To find the sum of all multiples of 3 less than 1000 that give an odd remainder when divided by 11, we need to follow these steps:
**Step 1: Find the multiples of 3 less than 1000:**
We need to find all the numbers that are divisible by 3 and less than 1000. We can use the formula for finding the sum of an arithmetic series to do this. The formula is given by:
*Sum = (n/2) * (first term + last term)*
In this case, the first term is 3, and we need to find the last term. The last term can be found by finding the largest multiple of 3 less than 1000. Divide 1000 by 3, and round down to the nearest whole number. Multiply this number by 3 to get the last term.
1000 / 3 = 333.33
Round down to 333
Last term = 333 * 3 = 999
Therefore, the sum of all multiples of 3 less than 1000 is given by:
Sum = (333/2) * (3 + 999) = 166.5 * 1002 = 166,833
**Step 2: Find the odd remainders when divided by 11:**
Next, we need to find which multiples of 3 give an odd remainder when divided by 11. We can do this by checking if the remainder of the division is odd. If the remainder is odd, we include the number in our sum.
Let's check the remainders by dividing each multiple of 3 by 11:
3 % 11 = 3 (odd remainder)
6 % 11 = 6 (even remainder)
9 % 11 = 9 (odd remainder)
12 % 11 = 1 (odd remainder)
15 % 11 = 4 (even remainder)
...
From this pattern, we can see that the multiples of 3 that give an odd remainder when divided by 11 have a difference of 3. We can use this information to find the sum of these multiples.
**Step 3: Find the sum of multiples with odd remainders:**
To find the sum of the multiples with odd remainders, we can use the formula for the sum of an arithmetic series again. This time, the first term is 3 (the first multiple of 3 with an odd remainder), and the last term is 999 (the last multiple of 3 less than 1000).
Using the formula, the sum of the multiples with odd remainders is given by:
Sum = (n/2) * (first term + last term)
= (n/2) * (3 + 999)
To find the value of n (the number of terms), we can use the formula for the nth term of an arithmetic series:
nth term = first term + (n - 1) * difference
In this case, the difference is 3 (the difference between consecutive multiples with odd remainders), and we need to find the largest multiple with an odd remainder less than 1000. Divide 1000 by 3, and round down to the nearest whole number. Subtract 1 from this number to get the value of n.
1000 / 3 = 333.33
Round down to 333
n
To find the sum of all multiples of 3 less than 1000 that give an odd remainder when divided by 11, we need to follow these steps:
**Step 1: Find the multiples of 3 less than 1000:**
We need to find all the numbers that are divisible by 3 and less than 1000. We can use the formula for finding the sum of an arithmetic series to do this. The formula is given by:
*Sum = (n/2) * (first term + last term)*
In this case, the first term is 3, and we need to find the last term. The last term can be found by finding the largest multiple of 3 less than 1000. Divide 1000 by 3, and round down to the nearest whole number. Multiply this number by 3 to get the last term.
1000 / 3 = 333.33
Round down to 333
Last term = 333 * 3 = 999
Therefore, the sum of all multiples of 3 less than 1000 is given by:
Sum = (333/2) * (3 + 999) = 166.5 * 1002 = 166,833
**Step 2: Find the odd remainders when divided by 11:**
Next, we need to find which multiples of 3 give an odd remainder when divided by 11. We can do this by checking if the remainder of the division is odd. If the remainder is odd, we include the number in our sum.
Let's check the remainders by dividing each multiple of 3 by 11:
3 % 11 = 3 (odd remainder)
6 % 11 = 6 (even remainder)
9 % 11 = 9 (odd remainder)
12 % 11 = 1 (odd remainder)
15 % 11 = 4 (even remainder)
...
From this pattern, we can see that the multiples of 3 that give an odd remainder when divided by 11 have a difference of 3. We can use this information to find the sum of these multiples.
**Step 3: Find the sum of multiples with odd remainders:**
To find the sum of the multiples with odd remainders, we can use the formula for the sum of an arithmetic series again. This time, the first term is 3 (the first multiple of 3 with an odd remainder), and the last term is 999 (the last multiple of 3 less than 1000).
Using the formula, the sum of the multiples with odd remainders is given by:
Sum = (n/2) * (first term + last term)
= (n/2) * (3 + 999)
To find the value of n (the number of terms), we can use the formula for the nth term of an arithmetic series:
nth term = first term + (n - 1) * difference
In this case, the difference is 3 (the difference between consecutive multiples with odd remainders), and we need to find the largest multiple with an odd remainder less than 1000. Divide 1000 by 3, and round down to the nearest whole number. Subtract 1 from this number to get the value of n.
1000 / 3 = 333.33
Round down to 333
n
|
Explore Courses for CAT exam
|
|
Similar CAT Doubts
Top Courses for CATView all
What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer?
Question Description
What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer?.
What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer?.
Solutions for What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer?, a detailed solution for What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer? has been provided alongside types of What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice What is the sum of all multiples of 3 less than 1000 which give an odd remainder when divided by 11 ?Correct answer is '75837'. Can you explain this answer? tests, examples and also practice CAT tests.
|
|
Explore Courses for CAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup