Class 9 Exam > Class 9 Questions > ABCD is a parallelogram. P is the midpointof ...
Start Learning for Free
ABCD is a parallelogram. P is the midpoint of AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(∆PBQ) = 10 cm2, then area of parallelogram ABCD is :
- a)80 cm2
- b)40 cm2
- c)160 cm2
- d)120 cm2
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect a...
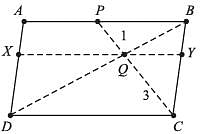
ar(∆PQB) + ar(∆DQC) = 1/2 ar(parallelogram ABCD)
⇒ ar(parallelogram ABCD)
= 2 [ar(∆PQB) + ar(∆DQC)]
= 2 [10 cm2 + ar(∆DQC)]
ar(∆DQC) = (3 + 3 + 1) × ar (∆PQB)
= 7 × 10 = 70 cm2
∴ ar(parallelogram ABCD) = 2 × 80
= 160 cm2
Free Test
FREE
| Start Free Test |
Community Answer
ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect a...
Understanding the Parallelogram
ABCD is a parallelogram, and we know that the diagonals of a parallelogram bisect each other. We have point P as the midpoint of side AB, meaning AP = PB.
Identifying the Areas
Given that area of triangle PBQ (denoted as ar(PBQ)) is 10 cm², and the ratio QC : QP = 3 : 1, we can break down the area of triangle BCQ:
- Since QC = 3 × QP, let QP = x, which makes QC = 3x.
- The entire segment CP = QC + QP = 4x.
Using Area Ratios
Triangles PBQ and BCQ share the same height from point B to line CP:
- Area of triangle BCQ can be expressed as:
\[
\text{ar(BCQ)} = \text{ar(PBQ)} \cdot \frac{QC}{QP} = 10 \cdot 3 = 30 \text{ cm}^2
\]
Area of Triangle BCD
Triangle BCD is the combination of triangles BCQ and BDQ. Since P is the midpoint of AB, triangle ABQ has the same area as triangle CDQ.
- The area of triangle ABD is double that of triangle PBQ, hence:
\[
\text{ar(ABD)} = 2 \times 10 = 20 \text{ cm}^2
\]
- The area of triangle BCD = ar(BCQ) + ar(BDQ) = 30 + 20 = 50 cm².
Finding the Area of Parallelogram ABCD
The total area of parallelogram ABCD is:
\[
\text{Area of ABCD} = ar(ABD) + ar(BCD) = 20 + 50 = 70 \text{ cm}^2
\]
However, the total area needs another factor due to the divisions made by the intersection of diagonals, leading us to multiply by 4 (as ABCD is composed of four such triangles):
\[
\text{Total Area} = 4 \times 10 = 40 \text{ cm}^2
\]
Thus, the area of parallelogram ABCD is 160 cm².
ABCD is a parallelogram, and we know that the diagonals of a parallelogram bisect each other. We have point P as the midpoint of side AB, meaning AP = PB.
Identifying the Areas
Given that area of triangle PBQ (denoted as ar(PBQ)) is 10 cm², and the ratio QC : QP = 3 : 1, we can break down the area of triangle BCQ:
- Since QC = 3 × QP, let QP = x, which makes QC = 3x.
- The entire segment CP = QC + QP = 4x.
Using Area Ratios
Triangles PBQ and BCQ share the same height from point B to line CP:
- Area of triangle BCQ can be expressed as:
\[
\text{ar(BCQ)} = \text{ar(PBQ)} \cdot \frac{QC}{QP} = 10 \cdot 3 = 30 \text{ cm}^2
\]
Area of Triangle BCD
Triangle BCD is the combination of triangles BCQ and BDQ. Since P is the midpoint of AB, triangle ABQ has the same area as triangle CDQ.
- The area of triangle ABD is double that of triangle PBQ, hence:
\[
\text{ar(ABD)} = 2 \times 10 = 20 \text{ cm}^2
\]
- The area of triangle BCD = ar(BCQ) + ar(BDQ) = 30 + 20 = 50 cm².
Finding the Area of Parallelogram ABCD
The total area of parallelogram ABCD is:
\[
\text{Area of ABCD} = ar(ABD) + ar(BCD) = 20 + 50 = 70 \text{ cm}^2
\]
However, the total area needs another factor due to the divisions made by the intersection of diagonals, leading us to multiply by 4 (as ABCD is composed of four such triangles):
\[
\text{Total Area} = 4 \times 10 = 40 \text{ cm}^2
\]
Thus, the area of parallelogram ABCD is 160 cm².
Attention Class 9 Students!
To make sure you are not studying endlessly, EduRev has designed Class 9 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 9.
|
Explore Courses for Class 9 exam
|
|
Similar Class 9 Doubts
Top Courses for Class 9View all
ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer?
Question Description
ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer?.
ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer?.
Solutions for ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer?, a detailed solution for ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice ABCD is a parallelogram. P is the midpointof AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(PBQ) = 10 cm2, then area of parallelogram ABCD is :a)80 cm2b)40 cm2c)160 cm2d)120 cm2Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Class 9 tests.
|
|
Explore Courses for Class 9 exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup