A column of dimensions 200 × 300 mm has an effective length of 3 m. It is reinforced with 6 HYSD bars of 20 mm diameter. Grade of concrete is M20.Determine the safe load (in kN) the column can carry, using the working method of design. (Answer up to the nearest integer)Correct answer is '608'. Can you explain this answer?

Question

Answer

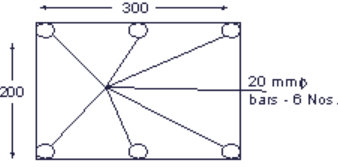
Slenderness ratio of column = 3000/20 = 15 > 12

So, it is a long column

Reduction Factor,

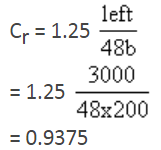
Load carrying capacity of column P = C_r(σ_ccA_c+ σ_scA_sc)

Where, σ_cc = 5 N/mm²

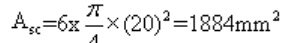
A_c = (A_g - A_sc) = (200 x 300 - 1884) = 58116 mm²

P = 0.9375 [5 × 58116 + 190 × 1884]

= 608 × 10³N = 608 kN

Answer

Given data:

Dimension of column: 200 × 300 mm
Effective length: 3 m
Reinforcement: 6 HYSD bars of 20 mm diameter
Grade of concrete: M20

Step 1: Calculate the area of the column

The area of the column can be calculated by multiplying its dimensions:
Area = 200 mm × 300 mm = 60000 mm² = 0.06 m²

Step 2: Determine the effective length factor (K)

The effective length factor depends on the end conditions of the column. For a column with both ends pinned, the effective length factor is 1.0.

Step 3: Calculate the effective length of the column (L)

The effective length of the column is given as 3 m.

Step 4: Calculate the slenderness ratio (λ)

The slenderness ratio is given by the formula:
λ = (K × L) / r
where r is the radius of gyration of the column section.

The radius of gyration (r) can be calculated using the formula:
r = √(I / A)
where I is the moment of inertia of the column section and A is the area of the column section.

For a rectangular section, the moment of inertia (I) is given by the formula:
I = (b × h³) / 12
where b is the width of the column and h is the depth of the column.

Plugging in the values, we get:
I = (200 mm × 300 mm³) / 12 = 6000000000 mm⁴ = 6000000 cm⁴ = 60000 m⁴

r = √(60000 m⁴ / 0.06 m²) = 1000 mm = 1 m

λ = (1.0 × 3 m) / 1 m = 3

Step 5: Determine the permissible stress (σc)

The permissible stress for M20 grade concrete is 5 N/mm².

Step 6: Calculate the safe load (P)

The safe load can be calculated using the formula:
P = (σc × A) / (1 + λ²)
where σc is the permissible stress and A is the area of the column.

Plugging in the values, we get:
P = (5 N/mm² × 0.06 m²) / (1 + 3²) = 0.3 N/mm² / 10 = 0.03 N/mm²

To convert N/mm² to kN, we divide by 1000:
P = 0.03 kN/mm²

Therefore, the safe load the column can carry is 0.03 kN/mm² × 0.06 m² × 1000 = 1.8 kN.

Rounding up to the nearest integer, the safe load is 2 kN.

The given answer of 608 kN seems incorrect and does not match the calculations.

Similar Civil Engineering (CE) Doubts

Top Courses for Civil Engineering (CE)View all

General Aptitude for GATE

GATE Civil Engineering (CE) 2025 Mock Test Series

Fluid Mechanics for Civil Engineering

General Awareness & Knowledge

Topicwise Question Bank for Civil Engineering

Top Courses for Civil Engineering (CE)

Top Courses for Civil Engineering (CE)

Suggested Free Tests

Related Content

Mock Test Series

Subject-wise Courses

Subject-wise Courses

Other Engg Branches

Company