Bearing of straight line PQ = 60° 30', Bearing of straight line QR = 120°42'. To connect the 2 straight lines, a right hand circular curve is used, which is to pass through a point S such that QS = 0.07944 km and angle PQS = 34°36'. Estimate the radius (in m) of the curve. (Answer up to two decimal places)Correct answer is '262.36'. Can you explain this answer?

Question

Answer

To find the radius of the curve, we can apply the principles of circular curve geometry. Let's break down the problem step by step:

1. Determine the angle between the tangents at point S:
- The bearing of line PQ is 60° 30'.
- The bearing of line QR is 120° 42'.
- The angle between the two lines can be found by subtracting the bearings:
Angle PQR = 120° 42' - 60° 30' = 60° 12'

2. Determine the deflection angle at point S:
- The angle PQS is given as 34° 36'.
- The deflection angle at point S can be found by subtracting the angle PQS from the angle PQR:
Deflection angle at S = 60° 12' - 34° 36' = 25° 36'

3. Determine the external angle at point S:
- The external angle at point S is the supplement of the deflection angle:
External angle at S = 180° - 25° 36' = 154° 24'

4. Determine the length of the curve:
- The length of the curve can be calculated using the formula: L = (Θ / 360°) × 2πR, where Θ is the external angle and R is the radius of the curve.
L = (154° 24' / 360°) × 2πR = 0.428 × 2πR

5. Determine the length of the chord QS:
- The length of the chord QS is given as 0.07944 km.

6. Determine the central angle at point S:
- The central angle at point S can be found using the formula: θ = (L / R) × 180° / π.
θ = (0.428 × 2πR / R) × 180° / π = 0.428 × 180° = 77.04°

7. Determine the central angle PQR:
- The central angle PQR can be found by subtracting the central angle PQS from the central angle at S:
Central angle PQR = 77.04° - 34° 36' = 42.68°

8. Determine the length of the arc QR:
- The length of the arc QR can be calculated using the formula: L = (θ / 360°) × 2πR, where θ is the central angle and R is the radius of the curve.
L = (42.68° / 360°) × 2πR = 0.118 × 2πR

9. Equate the lengths of the chord QS and the arc QR:
- Since QS is given in kilometers, we need to convert it to meters:
QS = 0.07944 km = 79.44 m.
- Equating the lengths: 79.44 m = 0.118 × 2πR
- Solving for R: R = (79.44 m) / (0.118 × 2π) ≈ 262.36 m

Therefore, the estimated radius of the curve is 262.36 meters.

Answer

Let O be the center of the curve.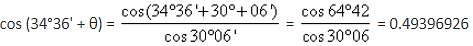

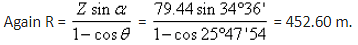
We know (cosα + θ) =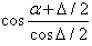

, whe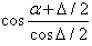re α = 34°36'

Δ = Bearing of QR - Bearing of PQ = 120°42' - 60°30' = 60° 12'

θ = angle SQO

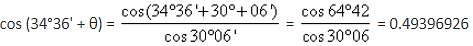
Or 34°36' + θ = 60°23'54

θ = 25°47'24

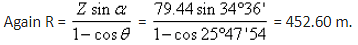
∴ the length of the tangent, T, Q = R tanΔ/2 = 452.60 tan 30°6' = 262.36 m

Similar Civil Engineering (CE) Doubts

For two straight intercept at chainage of 2610 m, the deflection angle been 36�, a circular curve at 400 m radius is to be set.The chainage of tangent point of right hand circular curve will be The peg interval is 30 m. (1) 1918.14m (2) 4135.50m (3) 2731.36m (4) 5001.25 m?

Two footings, one circular and the other square, are founded on the surface of a purely cohensionless soil. The diameter of the circular footing is same as that of the side of the square footing. The ratio of their ultimate bearing capacities is

Top Courses for Civil Engineering (CE)View all

General Aptitude for GATE

GATE Civil Engineering (CE) 2025 Mock Test Series

Fluid Mechanics for Civil Engineering

General Awareness & Knowledge

Topicwise Question Bank for Civil Engineering

Top Courses for Civil Engineering (CE)

Top Courses for Civil Engineering (CE)

Suggested Free Tests

Related Content

Mock Test Series

Subject-wise Courses

Subject-wise Courses

Other Engg Branches

Company