Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Which of the properties hold for the adjacenc...
Start Learning for Free
Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?
- a)The diagonal entries of A2 are the degrees of the vertices of the graph
- b)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic
- c)If the graph is connected then none of the entries of An-1 + In can be zero
- d)If there is at least a 1 in each of A's rows and columns, then the graph must be connected
Correct answer is option 'A,C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
Which of the properties hold for the adjacency matrix A of a simple un...
Option A : True
Let’s think about what (A2)i,i , the i - th term on the diagonal is. We have
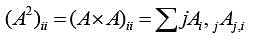
But Aij =Aj , i, assuming that the graph is undirected, and Aji = 1(i ~ j), i.e. is 1 is i and j are adjacent and 0 otherwise. Thus AijAj,i = A2i,j = Ai,j = 1(i ~ j) So the sum is just the number of j such that i ~ j, which
precisely the degree is.
This work if vertices in your graph may have a single self-loop, provided you count that as 1 (not 2) for the degree. Indeed, the term in the sum when j = i is just A2i,i, but you need this to be equal to Ai,i.
Thus it needs to be 0 or 1.
It does not work more generally, however, as A2ii ≠ Ai,j if Ai,j > 1.
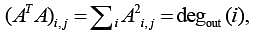
even for an undirected graph, provided the graph is simple.
Option : B False.
A cyclic graph is a graph containing at least one graph cycle. Consider a graph with 10 vertices where only three vertices form a cycle while reset are isolated vertices (that is a disconnected graph)
In such a case, sum of all the elements of A is (1 + 1 + 1) = 3 and 3 is less than 2 (10 -1) = 2 * 9 = 18. But the graph is still cyclic.
Option C : True.
The matrix An-1 + In represents number paths upto length n - 1 between pair of vertices, for a connected graph there will be at least one path between each pair of vertices, thus all entries of An-1 + In will be non zero.
Option D : False
Considering the following adjacency matrix :
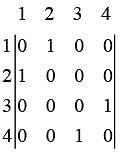
The corresponding graph is :


The graph is not connected
Let’s think about what (A2)i,i , the i - th term on the diagonal is. We have
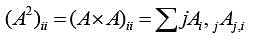
But Aij =Aj , i, assuming that the graph is undirected, and Aji = 1(i ~ j), i.e. is 1 is i and j are adjacent and 0 otherwise. Thus AijAj,i = A2i,j = Ai,j = 1(i ~ j) So the sum is just the number of j such that i ~ j, which
precisely the degree is.
This work if vertices in your graph may have a single self-loop, provided you count that as 1 (not 2) for the degree. Indeed, the term in the sum when j = i is just A2i,i, but you need this to be equal to Ai,i.
Thus it needs to be 0 or 1.
It does not work more generally, however, as A2ii ≠ Ai,j if Ai,j > 1.
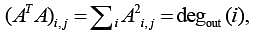
even for an undirected graph, provided the graph is simple.
Option : B False.
A cyclic graph is a graph containing at least one graph cycle. Consider a graph with 10 vertices where only three vertices form a cycle while reset are isolated vertices (that is a disconnected graph)
In such a case, sum of all the elements of A is (1 + 1 + 1) = 3 and 3 is less than 2 (10 -1) = 2 * 9 = 18. But the graph is still cyclic.
Option C : True.
The matrix An-1 + In represents number paths upto length n - 1 between pair of vertices, for a connected graph there will be at least one path between each pair of vertices, thus all entries of An-1 + In will be non zero.
Option D : False
Considering the following adjacency matrix :

The corresponding graph is :


The graph is not connected
Attention Computer Science Engineering (CSE) Students!
To make sure you are not studying endlessly, EduRev has designed Computer Science Engineering (CSE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Computer Science Engineering (CSE).

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Similar Computer Science Engineering (CSE) Doubts
Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer?
Question Description
Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer?.
Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer?.
Solutions for Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer?, a detailed solution for Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer? has been provided alongside types of Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?a)The diagonal entries of A2 are the degrees of the vertices of the graphb)If the sum of all the elements of A is at most 2(n -1) then the graph must be acyclic c)If the graph is connected then none of the entries of An-1 + In can be zerod)If there is at least a 1 in each of As rows and columns, then the graph must be connectedCorrect answer is option 'A,C'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























