Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Questions > The final code after encoding data bits 1101 ...
Start Learning for Free
The final code after encoding data bits 1101 into 7-bit even parity Hamming Code is
- a)1110101
- b)1011101
- c)1010101
- d)0110101
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
The final code after encoding data bits 1101 into 7-bit even parity Ha...
The given question belongs to the field of electronics and communication engineering and specifically deals with Hamming Code. Hamming Code is a technique used for error detection and correction in data transmission.
To understand the answer, let's break down the steps involved in encoding the data bits using Hamming Code:
1. Identify the number of parity bits required:
- The number of parity bits needed is determined by the formula 2^r ≥ m + r + 1, where r is the number of parity bits and m is the number of data bits.
- In this case, we have 4 data bits (1101), so we need to find the smallest value of r that satisfies the equation. By substituting different values of r, we find that r = 3 is the minimum value that satisfies the equation.
2. Insert the data bits into the encoded bit positions:
- The data bits are inserted into the encoded bit positions, leaving spaces for the parity bits.
- The data bits are placed in the positions that are powers of 2 (1, 2, 4, 8, etc.), starting from the leftmost position.
- In this case, the data bits 1101 are inserted into the positions 1, 2, 4, and 8, respectively.
3. Calculate the value of each parity bit:
- Each parity bit is responsible for checking a specific set of bits, including itself.
- The value of each parity bit is determined by performing an XOR operation on the bits it checks.
- The parity bits are placed in the positions that are not powers of 2.
- In this case, the parity bits are placed in positions 3, 5, and 6, respectively.
4. Determine the value of each parity bit:
- The value of each parity bit is determined by counting the number of 1s in the positions it checks.
- If the count is even, the parity bit is set to 0. If the count is odd, the parity bit is set to 1.
- In this case, the count of 1s in positions 3, 5, and 6 is 2, 2, and 1, respectively.
- Therefore, the parity bits are set to 0, 0, and 1, respectively.
5. Combine the data bits and parity bits to form the final encoded code:
- The data bits and parity bits are combined to form the final encoded code.
- In this case, the final encoded code is 1010101.
Therefore, the correct answer is option 'C' (1010101).
To understand the answer, let's break down the steps involved in encoding the data bits using Hamming Code:
1. Identify the number of parity bits required:
- The number of parity bits needed is determined by the formula 2^r ≥ m + r + 1, where r is the number of parity bits and m is the number of data bits.
- In this case, we have 4 data bits (1101), so we need to find the smallest value of r that satisfies the equation. By substituting different values of r, we find that r = 3 is the minimum value that satisfies the equation.
2. Insert the data bits into the encoded bit positions:
- The data bits are inserted into the encoded bit positions, leaving spaces for the parity bits.
- The data bits are placed in the positions that are powers of 2 (1, 2, 4, 8, etc.), starting from the leftmost position.
- In this case, the data bits 1101 are inserted into the positions 1, 2, 4, and 8, respectively.
3. Calculate the value of each parity bit:
- Each parity bit is responsible for checking a specific set of bits, including itself.
- The value of each parity bit is determined by performing an XOR operation on the bits it checks.
- The parity bits are placed in the positions that are not powers of 2.
- In this case, the parity bits are placed in positions 3, 5, and 6, respectively.
4. Determine the value of each parity bit:
- The value of each parity bit is determined by counting the number of 1s in the positions it checks.
- If the count is even, the parity bit is set to 0. If the count is odd, the parity bit is set to 1.
- In this case, the count of 1s in positions 3, 5, and 6 is 2, 2, and 1, respectively.
- Therefore, the parity bits are set to 0, 0, and 1, respectively.
5. Combine the data bits and parity bits to form the final encoded code:
- The data bits and parity bits are combined to form the final encoded code.
- In this case, the final encoded code is 1010101.
Therefore, the correct answer is option 'C' (1010101).
Free Test
FREE
| Start Free Test |
Community Answer
The final code after encoding data bits 1101 into 7-bit even parity Ha...
Hamming (7, 4) code: It is a linear error-correcting code that encodes four bits of data into seven bits, by adding three parity bits.
Example: It is used in the Bell-Telephone laboratory, error-prone punch caret reader to detect the error and correct them.
Hamming code:
P1 = d1 ⊕ d2 ⊕ d4
P2 = d1 ⊕ d4 ⊕ d3
P3 = d2 ⊕ d4 ⊕ d3
Example: It is used in the Bell-Telephone laboratory, error-prone punch caret reader to detect the error and correct them.
Hamming code:
P1 = d1 ⊕ d2 ⊕ d4
P2 = d1 ⊕ d4 ⊕ d3
P3 = d2 ⊕ d4 ⊕ d3
Given data 1101 i.e.
d1 = 1, d2 = 1, d3 = 0, d4 = 1
We can write:
P1 = d1 ⊕ d2 ⊕ d4 = 1 ⊕ 1 ⊕ 1 = 1
P2 = d1 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
P3 = d2 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
Then transmitted final code is
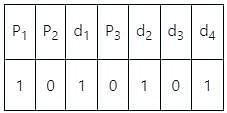
i.e. 1010101
Option 3 correct.
d1 = 1, d2 = 1, d3 = 0, d4 = 1
We can write:
P1 = d1 ⊕ d2 ⊕ d4 = 1 ⊕ 1 ⊕ 1 = 1
P2 = d1 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
P3 = d2 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
Then transmitted final code is
i.e. 1010101
Option 3 correct.
Attention Electronics and Communication Engineering (ECE) Students!
To make sure you are not studying endlessly, EduRev has designed Electronics and Communication Engineering (ECE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Electronics and Communication Engineering (ECE).
|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|
|
Similar Electronics and Communication Engineering (ECE) Doubts
Top Courses for Electronics and Communication Engineering (ECE)View all
The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer?
Question Description
The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2024 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer?.
The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2024 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer?.
Solutions for The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electronics and Communication Engineering (ECE).
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Here you can find the meaning of The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer?, a detailed solution for The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The final code after encoding data bits 1101 into 7-bit even parity Hamming Code isa)1110101b)1011101c)1010101d)0110101Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Electronics and Communication Engineering (ECE) tests.
|
|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
x
![]()
For Your Perfect Score in Electronics and Communication Engineering (ECE)
The Best you need at One Place
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup