CAT Exam > CAT Questions > If r is a constant such that x2 − 4x &m...
Start Learning for Free
If r is a constant such that ∣x2 − 4x − 13∣ = r has exactly three distinct real roots, then the value of r is
- a)17
- b)21
- c)15
- d)18
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
If r is a constant such that x2 − 4x − 13 = r has exactly ...
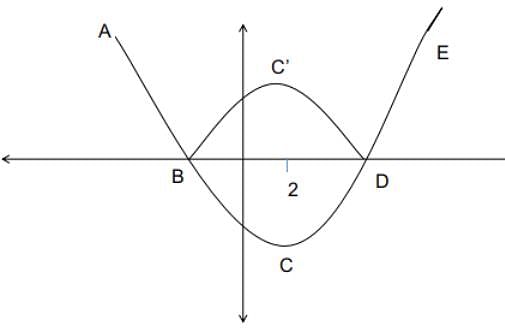
The quadratic equation of the form ∣x2 − 4x − 13∣ = r has its minimum value at x = -b/2a, and hence does not vary irrespective of the value of x.
Hence at x = 2 the quadratic equation has its minimum.
Considering the quadratic part : |x2 − 4 ⋅ x − 13|. as per the given condition, this must-have 3 real roots.
The curve ABCDE represents the function |x2 − 4 ⋅ x − 13|. Because of the modulus function, the representation of the quadratic equation becomes:
ABC'DE.
There must exist a value, r such that there must exactly be 3 roots for the function. If r = 0 there will only be 2 roots, similarly for other values there will either be 2 or 4 roots unless at the point C'.
The point C' is a reflection of C about the x-axis. r is the y coordinate of the point C':
The point C which is the value of the function at x = 2, = 22 − 8 − 13
= -17, the reflection about the x-axis is 17.
Alternatively,
|x2 - 4x - 13| = r
This can represented in two parts :
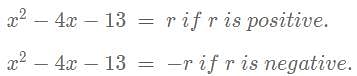
Considering the first case : x2 − 4x − 13 = r
The quadraticequation becomes : x2 − 4x − 13 − r = 0
The discriminant for this function is : b2 − 4ac = 16− (4⋅(−13 − r)) = 68 + 4r
SInce r is positive the discriminant is always greater than 0 this must have two distinct roots.
For the second case :
x2 − 4x − 13 + r = 0 the function inside the modulus is negaitve
The discriminant is 16 − (4⋅(r−13)) = 68−4r
In order to have a total of 3 roots, the discriminant must be equal to zero for this quadratic equation to have a total of 3 roots.
Hence 68 − 4r = 0
r = 17, for r = 17 we can have exactly 3 roots.
Most Upvoted Answer
If r is a constant such that x2 − 4x − 13 = r has exactly ...
Understanding the Problem
To find the value of r such that the equation x² - 4x - 13 = r has exactly three distinct real roots, we can rearrange it to form a standard quadratic equation.
Rearranging the Equation
The equation can be rewritten as:
x² - 4x - (r + 13) = 0.
This is a quadratic equation in the standard form ax² + bx + c = 0, where:
- a = 1
- b = -4
- c = -(r + 13)
Condition for Roots
For a quadratic equation to have distinct real roots, the discriminant (D) must be positive:
D = b² - 4ac > 0.
Since we need exactly three distinct real roots, we will first consider the case where one root is a double root, and the other is a distinct root.
Discriminant Calculation
Substituting values into the discriminant formula:
D = (-4)² - 4(1)(-(r + 13)) > 0.
This simplifies to:
16 + 4(r + 13) > 0.
Rearranging gives us:
4r + 64 > 0.
Finding the Values of r
Solving for r, we get:
r + 16 > 0, or r > -16.
Now, for the scenario where we have exactly three distinct real roots, the discriminant must be equal to zero for one root and positive for the other. Hence:
4r + 64 = 0 (double root condition).
Solving gives:
4r = -64, leading to r = -16.
Identifying the Correct Value of r
Now we analyze the roots for specific values of r given in the options. Testing r = 17:
Substituting r = 17:
D becomes:
16 + 4(17 + 13) = 16 + 4(30) = 16 + 120 = 136 > 0.
This indicates two distinct roots.
So, the correct answer is:
Conclusion
The value of r that gives exactly three distinct real roots is:
r = 17 (Option A).
To find the value of r such that the equation x² - 4x - 13 = r has exactly three distinct real roots, we can rearrange it to form a standard quadratic equation.
Rearranging the Equation
The equation can be rewritten as:
x² - 4x - (r + 13) = 0.
This is a quadratic equation in the standard form ax² + bx + c = 0, where:
- a = 1
- b = -4
- c = -(r + 13)
Condition for Roots
For a quadratic equation to have distinct real roots, the discriminant (D) must be positive:
D = b² - 4ac > 0.
Since we need exactly three distinct real roots, we will first consider the case where one root is a double root, and the other is a distinct root.
Discriminant Calculation
Substituting values into the discriminant formula:
D = (-4)² - 4(1)(-(r + 13)) > 0.
This simplifies to:
16 + 4(r + 13) > 0.
Rearranging gives us:
4r + 64 > 0.
Finding the Values of r
Solving for r, we get:
r + 16 > 0, or r > -16.
Now, for the scenario where we have exactly three distinct real roots, the discriminant must be equal to zero for one root and positive for the other. Hence:
4r + 64 = 0 (double root condition).
Solving gives:
4r = -64, leading to r = -16.
Identifying the Correct Value of r
Now we analyze the roots for specific values of r given in the options. Testing r = 17:
Substituting r = 17:
D becomes:
16 + 4(17 + 13) = 16 + 4(30) = 16 + 120 = 136 > 0.
This indicates two distinct roots.
So, the correct answer is:
Conclusion
The value of r that gives exactly three distinct real roots is:
r = 17 (Option A).
|
Explore Courses for CAT exam
|
|
Similar CAT Doubts
Top Courses for CATView all
If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer?
Question Description
If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer?.
If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer?.
Solutions for If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer?, a detailed solution for If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If r is a constant such that x2 − 4x − 13 = r has exactly three distinct real roots, then the value of r isa)17b)21c)15d)18Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice CAT tests.
|
|
Explore Courses for CAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup