NEET Exam > NEET Questions > The half life of radioactive radon is 3.8 day...
Start Learning for Free
The half life of radioactive radon is 3.8 days . The time , at end of which 1/20th
of radon sample will remain undecayed is
of radon sample will remain undecayed is
Verified Answer
The half life of radioactive radon is 3.8 days . The time , at end of ...
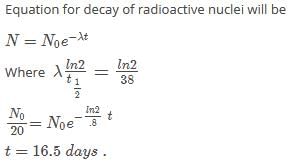
 This question is part of UPSC exam. View all NEET courses
This question is part of UPSC exam. View all NEET courses
Most Upvoted Answer
The half life of radioactive radon is 3.8 days . The time , at end of ...
The half-life of a radioactive substance is the time it takes for half of the atoms in a sample to decay. In the case of radioactive radon, its half-life is 3.8 days. This means that after 3.8 days, half of the radon atoms in a sample will have decayed, and after another 3.8 days, half of the remaining radon atoms will have decayed, and so on.
To find the time at which 1/20th of the radon sample will remain undecayed, we can use the concept of exponential decay. The formula for exponential decay is given by:
N(t) = N₀ * (1/2)^(t/T)
Where:
- N(t) is the number of undecayed atoms at time t
- N₀ is the initial number of undecayed atoms
- t is the time that has passed
- T is the half-life of the substance
Now let's break down the solution into steps:
1. Determine the fraction of undecayed radon atoms remaining after a given time.
- In this case, we want to find the time at which 1/20th (or 1/2^4) of the radon sample will remain undecayed. This means the fraction of undecayed atoms remaining is (1/2)^4.
2. Set up the exponential decay equation.
- Using the formula N(t) = N₀ * (1/2)^(t/T), we can substitute the fraction of undecayed atoms remaining into the equation. The equation becomes (1/2)^4 = N₀ * (1/2)^(t/3.8).
3. Solve for t.
- To find the value of t, we need to isolate it in the equation. We can do this by taking the logarithm of both sides of the equation. Using logarithm base 2 (since we have a fraction of 1/2), the equation becomes log₂((1/2)^4) = log₂(N₀ * (1/2)^(t/3.8)).
4. Simplify the equation.
- The logarithm of (1/2)^4 is equal to 4 times the logarithm of 1/2. Using the logarithmic property log₂(a^b) = b * log₂(a), the equation simplifies to 4 * log₂(1/2) = log₂(N₀ * (1/2)^(t/3.8)).
5. Solve for t.
- Now we can solve for t by dividing both sides of the equation by log₂(1/2). This gives us 4 = log₂(N₀ * (1/2)^(t/3.8)) / log₂(1/2). Using the logarithmic property log₂(a) / log₂(b) = log_b(a), the equation further simplifies to 4 = log(1/2) / log(2) * (t/3.8).
6. Calculate the value of t.
- Finally, we can solve for t by multiplying both sides of the equation by 3.8 and dividing by 4. This gives us t = (4 * log(1/2) / log(2)) * 3.8.
7. Evaluate the expression to find
To find the time at which 1/20th of the radon sample will remain undecayed, we can use the concept of exponential decay. The formula for exponential decay is given by:
N(t) = N₀ * (1/2)^(t/T)
Where:
- N(t) is the number of undecayed atoms at time t
- N₀ is the initial number of undecayed atoms
- t is the time that has passed
- T is the half-life of the substance
Now let's break down the solution into steps:
1. Determine the fraction of undecayed radon atoms remaining after a given time.
- In this case, we want to find the time at which 1/20th (or 1/2^4) of the radon sample will remain undecayed. This means the fraction of undecayed atoms remaining is (1/2)^4.
2. Set up the exponential decay equation.
- Using the formula N(t) = N₀ * (1/2)^(t/T), we can substitute the fraction of undecayed atoms remaining into the equation. The equation becomes (1/2)^4 = N₀ * (1/2)^(t/3.8).
3. Solve for t.
- To find the value of t, we need to isolate it in the equation. We can do this by taking the logarithm of both sides of the equation. Using logarithm base 2 (since we have a fraction of 1/2), the equation becomes log₂((1/2)^4) = log₂(N₀ * (1/2)^(t/3.8)).
4. Simplify the equation.
- The logarithm of (1/2)^4 is equal to 4 times the logarithm of 1/2. Using the logarithmic property log₂(a^b) = b * log₂(a), the equation simplifies to 4 * log₂(1/2) = log₂(N₀ * (1/2)^(t/3.8)).
5. Solve for t.
- Now we can solve for t by dividing both sides of the equation by log₂(1/2). This gives us 4 = log₂(N₀ * (1/2)^(t/3.8)) / log₂(1/2). Using the logarithmic property log₂(a) / log₂(b) = log_b(a), the equation further simplifies to 4 = log(1/2) / log(2) * (t/3.8).
6. Calculate the value of t.
- Finally, we can solve for t by multiplying both sides of the equation by 3.8 and dividing by 4. This gives us t = (4 * log(1/2) / log(2)) * 3.8.
7. Evaluate the expression to find

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is
Question Description
The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is.
The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is.
Solutions for The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is defined & explained in the simplest way possible. Besides giving the explanation of
The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is, a detailed solution for The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is has been provided alongside types of The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is theory, EduRev gives you an
ample number of questions to practice The half life of radioactive radon is 3.8 days . The time , at end of which 1/20thof radon sample will remain undecayed is tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























