Alpha Decay using the WKB Approximation | Physics Optional Notes for UPSC PDF Download
One of the early applications of the WKB approximation was George Gamow’s 1928 theory of alpha decay. In a large nucleus, the nucleons (protons and neutrons) are held together by the strong nuclear force which at short range is stronger than the electric repulsion between the protons. The strong nuclear force is very short range, however, so if some nucleons can tunnel through the potential barrier, the electric force rapidly takes over resulting in the nucleons being ejected from the nucleus.
A common mode of decay is the emission of an alpha particle, consisting of 2 neutrons and 2 protons (a helium-4 nucleus). Gamow’s model proposed that the nuclear force be modelled as a square well at potential -V0 and width r1 followed by the Coulomb repulsive potential for r > r1. That is
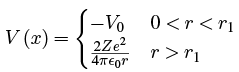
where Z is the number of protons in the nucleus of the atom remaining after the emission of the alpha particle. The 2 in the numerator is the number of protons in the alpha particle.
If the alpha particle has an energy E such that 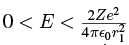 then its energy is below the maximum of V which occurs at r = r1, so in order for it to escape, it must tunnel through the potential in the region r1 < r < r2 where the outer radius r2 is determined by
then its energy is below the maximum of V which occurs at r = r1, so in order for it to escape, it must tunnel through the potential in the region r1 < r < r2 where the outer radius r2 is determined by
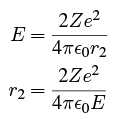
We saw that applying the WKB approximation to tunneling gave us a transmission probability of 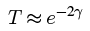
where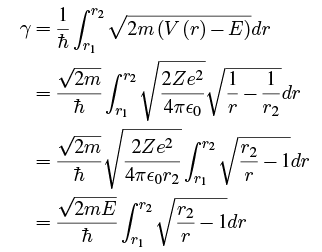 Doing the integral with Maple gives
Doing the integral with Maple gives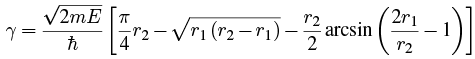 We can write this in terms of ρ = r1/r2:
We can write this in terms of ρ = r1/r2: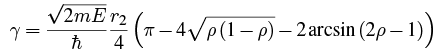 If we assume that r1<< r2 (that is, the range of the nuclear force is much less than the point where the alpha particle breaks free of the nucleus, which is usually the case), then a series expansion about ρ = 0 gives
If we assume that r1<< r2 (that is, the range of the nuclear force is much less than the point where the alpha particle breaks free of the nucleus, which is usually the case), then a series expansion about ρ = 0 gives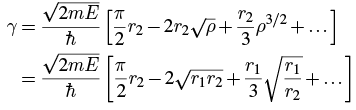 Taking just the first two terms, we have, using 3
Taking just the first two terms, we have, using 3 where the constants are
where the constants are Plugging in the numbers gives (in SI units; remember that m is the mass of the emitted alpha particle):
Plugging in the numbers gives (in SI units; remember that m is the mass of the emitted alpha particle): where the fm is a fermi or 10-15 m, so 1015 m-1 = 1 fm-1 and √1015 m-1/2 = 3.16 × 107 m-1/2 = 1 fm-1/2.
where the fm is a fermi or 10-15 m, so 1015 m-1 = 1 fm-1 and √1015 m-1/2 = 3.16 × 107 m-1/2 = 1 fm-1/2.
Example1: As a specific example, we’ll look at 238U. When this isotope of uranium emits an alpha particle, the remaining nucleus is 234Th (thorium). The masses can be found at this site, and we get
238U : 238.050782
234Th : 234.043595
4He : 4.002603
The masses are in unified atomic mass units (u), where one u is 1/12 the mass of 12C or 1.66 × 10-27 kg or 931.5 MeV.
Returning to 238U we need values for r1 and E. From experiment, we have
where A is the total number of protons and neutrons in the nucleus. From special relativity, we can get the energy of the emitted alpha particle as the difference between the rest masses of the parent nucleus m_p and those of the residual nucleus mr plus alpha particle mα:
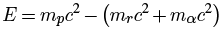
From the numbers above, we get:
r1 = 1.07 (238)1/3 = 6.63 fm
E = (238.050782 - 234.043595 - 4.002603) x 931.5 = 4.27 MeV
To calculate γ we use (15) with Z = 90 for the decay product (thorium), and we get: γ = 50.06
To get a prediction of the lifetime of a 238U nucleus, we can use a crude argument to get a rough estimate. Suppose that, before its escape, the alpha particle is moving within the nucleus with some velocity v, giving it a kinetic energy of: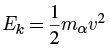
If we’re interested only in an order of magnitude estimate, we can ignore the nuclear binding energy -V0 within the nucleus and take E ≈ Ek. (In reality, E = Ek - V0, so making this assumption underestimates the velocity.) On average, the alpha particle will collide with the boundary (that is, it will reach r = r1) with a frequency of v/2r1} times per second (since it travels the diameter of the nucleus between collisions), and from (4), the probability of tunneling through the barrier is 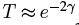 on each collision. Thus the probability of emission per second is about
on each collision. Thus the probability of emission per second is about 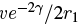 making the approximate lifetime τ of the parent nucleus equal to the reciprocal of this or:
making the approximate lifetime τ of the parent nucleus equal to the reciprocal of this or:
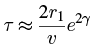
For 238U we get:
This is about 4% of the speed of light, so we’re justified in using a non-relativistic approximation. The lifetime is thus
The lifetime is thus
τ= 2.8 x 1022 , s = 8.87 x 1014 years
The actual half-life of 238U is around 4.5 × 109 years, so this estimate is pretty wide of the mark, but at least it agrees that the lifetime is very long.
Example2:We can do the same calculation for 212Po which decays to 208Pb and we find the atomic masses are
212Po : 211.988851
208Pb : 207.976635
Plugging in the numbers as before, we get
r₁ = 6.34 fm
E = 8.954 MeV
v = 2.079 × 10⁷ m s⁻¹
γ = 20.399
τ = 3.19 × 10⁻⁴ s
The experimental value is 3 × 10-7s so again the WKB calculation is quite a bit longer, but at least it gives good qualitative agreement. Because the dependence on γ (and thus on E , Z and r1 is exponential, relatively small changes in these quantities translate into a huge difference in lifetime.
FAQs on Alpha Decay using the WKB Approximation - Physics Optional Notes for UPSC
| 1. What is alpha decay and how does it occur? |  |
| 2. What is the WKB approximation in quantum mechanics? |  |
| 3. How does the WKB approximation apply to alpha decay? |  |
| 4. What role does quantum tunneling play in alpha decay? |  |
| 5. Why is the WKB approximation important for understanding alpha decay in nuclear physics? |  |





















