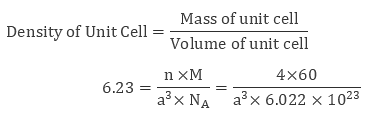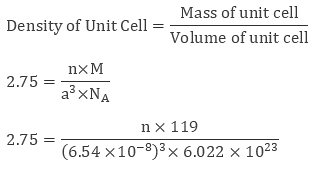Close Packed Structures, Packing Efficiency & Imperfections in Solids | Chemistry Class 12 - NEET PDF Download
What are Close Packed Structures?
In order to analyze the close packing of constituent particles (ions, molecules or atoms) in a lattice, we get into the assumption that constituent particles (ions, molecules or atoms) are hard spheres of identical shape.
 Different Types of Layers Forming Closed Packed Structures
Different Types of Layers Forming Closed Packed Structures
What is Close Packing?
The packing of constituent particles inside lattice in such a way that they occupy maximum available space in the lattice is known as Close Packing.
Close Packing is done in three ways, namely:
(a) One Dimensional Close Packing
(b) Two Dimensional Close Packing
(c) Three Dimensional Close Packing
(a) One Dimensional Close Packing
In one dimension close packing, the spheres are arranged in a row touching each other. In one-dimensional close packing, each sphere is in direct contact with two of its neighbor spheres. The number of nearest spheres to a particle in a lattice is called Coordination Number. Since there are two spheres in direct contact with the one sphere, the coordination number of one-dimensional close packing is 2.
(b) Two Dimensional Close Packing
Two-dimensional close packing is done by stacking rows of hard spheres one above the other. This can be done in two ways:
• AAA type
• ABA type
(i) AAA Type
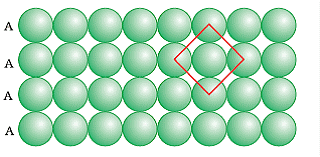 AA Type Packing
AA Type Packing
The packing in which one sphere touches two spheres placed in two different rows one above and one below is called AAA type close packing. The coordination number of AAA type two-dimensional close packing is 4. The AAA type is formed by placing one-dimensional row directly one above the other in both horizontal and vertical directions. It is also called two-dimensional square close packing as the rows of spheres when arranged in vertical and horizontal alignments form a square.
(ii) AB Type
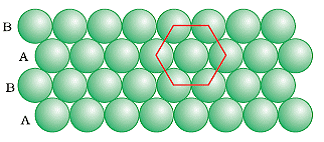 AB Type Packing
AB Type Packing
The packing in which the spheres in the second row are located in the depressions of the first row. The ABA type close packing is formed by placing one-dimensional row let’s say B type over the A type close packing and this series continues to form a two dimensional hexagonal. The coordination number of ABA Type packing is 6 as each sphere is in direct contact with 6 other spheres.
In ABA type close-packing we find triangular empty spaces called voids. These are of two types:
- Apex of triangle pointing upwards
- Apex of triangle pointing downwards
(c) Three Dimensional Close Packing
The formation of real lattices and structures take place through three-dimensional close packing. They are formed by stacking two-dimensional layers of spheres one above the other. This can be done by two ways:
- Three-dimensional close packing from two dimensional square close packed layers
- Three-dimensional close packing from two dimensional hexagonal close packed layers
Three-dimensional close packing from two-dimensional close packed layers
Formation of three-dimensional close packing can be done by placing the second square closed packing exactly above the first one. In this close packing, the spheres are aligned properly in horizontally and vertically. Similarly, by placing more layers one above the other, we can obtain a simple cubic lattice. The unit cell of the simple cubic lattice is called the primitive cubic unit cell.
Three-dimensional close packing from two dimensional hexagonal close-packed layers
Three-dimensional close packing can be formed with the help of two-dimensional hexagonal packed layers in two ways:
• Stacking the second layer over the first layer
• Stacking the third layer over the second layer
Stacking the second layer over the first layer
Suppose we take two hexagonal close packed layer ‘A’ and place it over the second layer B ( as both layers have different alignment of spheres) such that spheres of the second layer are placed in the depressions of the first layer. We observe that a tetrahedral void is formed when a sphere of the second layer is right above the void (empty space) of the first layer. Adding further we notice octahedral voids at the points where the triangular voids of the second layer are placed right triangular voids of the first one in such a way that triangular space doesn't overlap. Octahedral voids are bordered by six spheres.
 Types of Voids in three-dimensional Close PackingIf there are ‘N’ closed spheres, then:
Types of Voids in three-dimensional Close PackingIf there are ‘N’ closed spheres, then:
• Number of Octahedral Voids equals to “N”
• Number of Tetrahedral Voids equals to “ 2N”
Stacking the third layer over the second layer:
There are two possible ways of placing the third layer over the second layer:
(1) By Covering Tetrahedral Voids
(2) By Covering Octahedral Voids
(1) Covering Tetrahedral Voids
In this kind of three-dimensional packing, the spheres of the third layer are aligned right above the spheres of the first layer. If we name the first layer as A and second layer as B, then the pattern will be ABAB… so far and so forth. The structure formed is also called hexagonal close-packed structure also known as HCP.
(a) For HCP geometry Coordination number = 12
(b) For HCP geometry no. Of atoms per unit cell (corner) = 12 (corner)  (inside the body) ∗ 1 = 6
(inside the body) ∗ 1 = 6
(c) For HCP geometry packing efficiency = 74%
(2) Covering Octahedral Voids
In this kind of packing the third layer, spheres are not placed with either of the second layer or first layer. If we name the first layer as A, second as B and then the third layer will be C (as it is now a different layer) then the pattern will be ABCABC… The structure formed is also called cubic closed packed (ccp) or face-centred packed cubic structure (fcc). For Example metals like copper and iron crystallize in the structure.
The coordination number in both cases will be 12 as each sphere in the structure is in direct contact with 12 other spheres. The packing is highly efficient and around 74% of the crystal is completely occupied. ABC Type Close Packing
ABC Type Close Packing
The cubic close packing has face centred (fcc) unit cell.
(a) For CCP geometry coordination number = 12
(b) For CCP geometry number of atoms per unit cell = 4 (as calculated before)
(c) For CCP geometry packing efficiency = 74% (as calculated before) In the close packing of spheres, certain hollows are left vacant. These holes or voids in the crystals are called interstitial sites or interstitial voids.
Two important interstitial sites are:
(i) Triangular
(ii) Tetrahedral
(iii) Octahedral
(iv) Cubical void
The formula of a Compound and Number of Voids Filled
• The number of octahedral voids present in a lattice = The number of close-packed particles.
• The number of tetrahedral voids produced is twice this number.
• In ionic solids, the bigger ions i.e. anions forms close-packed structure and the smaller ions i.e. cations occupy the voids.
• If the latter ion is small then tetrahedral voids are occupied, if bigger, then octahedral voids are occupied.
• In a compound, the fraction of octahedral or tetrahedral voids that are occupied depends upon the chemical formula of the compound.
• Close packed structures have both tetrahedral and octahedral voids.
Calculations Involving Unit Cells Dimensions
With the help of geometry and attributes of unit cells, we can easily evaluate the volume of the unit cell. With the volume and mass of atoms, we can also evaluate the density of the unit cell. A crystal lattice is represented in terms of unit cells; we can determine the density of crystal lattices by evaluating the density of unit cells.
Volume Density
Formula volume density of metal:
| ρv = Mass per unit cell/Volume per unit cell |
The density of Unit Cell
A unit cell is a three-dimensional structure occupying one, two or more atoms. With the help of the dimensions of unit cells, we can evaluate the density of the unit cell. To do so let’s consider a unit cell of edge length ‘a’, therefore the volume of the cell will be ‘a3’. Also, density is defined as the ratio of the mass of the unit cell and volume of the unit cell.| Density of Unit Cell = mass of unit cell/Volume of unit cell |
Above equation is marked as equation 1.
Mass of unit cell varies with number of atoms “n” and mass of a single atom “m”. Mathematically mass of unit cell is the product of number of atoms “n” and mass of one atom “m” i.e.
| Mass of Unit Cell = n × m |
Also from quantitative aspect of atoms, mass of one atom can be written in terms of Avogadro Number ( NA ) and molar mass of atom ( M), that is,
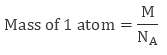
Volume of Unit Cell = a3
Placing the required values in equation 1 we get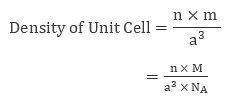
| Density of Unit Cell = n x M / (a3 x NA) |
Therefore if we know molar mass of atom “M”, number of atoms “n”, the edge length of unit cell “a” we can evaluate the density of unit cell.
Example 1: The density of a face-centered unit cell is 6.23 g cm-3. Given the atomic mass of a single atom is 60, evaluate the edge length of the unit cell. (Take value of NA = 6.022 × 1023).
Sol: As the unit cell is a face-centered unit cell, a number of atoms will be 4. We have
n = 4 , M = 60 , NA = 6.022 × 1023 and d = 6.23 g cm-3
We know that
After evaluating we get the value of edge length of the cube to be 4 × 10-8 cm.
Example 2: KBr or potassium bromide has density 2.75 g cm-3. The edge length of its unit cell is 654 pm. Prove that KBr depicts face-centered cubic structure.
Sol: We have edge length of unit cell = 654 pm = 6.54 × 10-8 cm
Therefore volume of the cell = (6.54 ×10-8)3 cm3
Molar Mass of Potassium Bromide ( KBr) is 119 g/mol
Density of KBr = 2.75 g cm-3
We know thatEvaluating we get value of n to be 3.09 ≈ 4
Since a number of atoms is 4 we can clearly say that KBr is a face-centred cubic structure.
Radius Ratio Rule and Calculations
The structure of each ionic compound is determined by stoichiometry and ion sizes. Larger cations can fit into cubic or octahedral holes. In tetrahedral holes, smaller cations can be accommodated. If we examine an array of anions in the form of cubic tight packing, the diameters of the tetrahedral and octahedral holes will vary. As a result, the cations will only occupy the voids if there is adequate room for them.
The Radius Ratio can be used to determine whether the ions will be able to retain the cations. The shape of the unit cell is also determined by the ion’s coordination number in the crystal structure. For a particular coordination number, there is a limiting value of the ratio of cation radius to anion radius, i.e. r+ / r–. The ionic structure becomes unstable if the value of the ratio r+ / r– is smaller than the predicted value.
Hence, the radius ratio is defined as the ratio of a smaller ionic radius (cation) to a larger ionic radius (anion), and is given by,
ρ = r+ / r–
where,
- ρ is the radius ratio,
- r+ is the radius of cation, and
- r– is the radius of the anion.
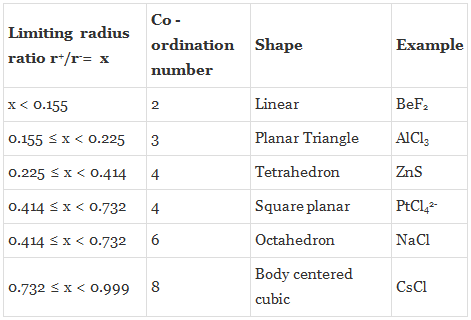
Given below are the limiting values of r+ / r– and their coordination numbers.

Examples are B2O3, ZnS, NaCl, CsCl, MgO, CuCl
Some properties are:
- The radius ratio rule only applies to ionic substances.
- If the bonds are covalent, the rule is broken.
- The rule may be used to predict the structures of various ionic solids.
Sample Problems
Problem 1: If a solid “X+Y–” has a structure similar to NaCl and the radius of anion is 250 pm. Then, find the ideal radius of the cation in the structure. Also, state your reason, is it possible to fit a cation Z+ of radius 180 pm in the tetrahedral site of the structure(X+Y–)?
Sol: Given that, Structure X+Y–
Radius of anion = 250 pm = 2.5 A° [1 picometer = 0.01A°]Limiting ratio = 0.414 [refer to the above table]
If the X+Y– structure is comparable to that of the Na+Cl– ion, then six Cl– ions will surround the Na+ and vice versa.
Thus, octahedral void is occupied.
Radius ration ρ = r+ / r–
r+ = 0.414 × 2.5 = 1.035 A°
Now, the limiting ratio for tetrahedral site is 0.225 [refer to table]
As a result, r+ / r– = 0.225
=> r+ = 0.225 × 2.5 = 0.5625 A° or 56.25 pm
Thus, for a tetrahedral site, the optimum radius for the cation in the given structure is 56.25 pm.
We know that the radius of Z+ is 180 pm. This implies that Z+‘s radius is substantially bigger than 56.25 pm.
Thus, cation Z+ cannot be accommodated in a tetrahedral location.
Problem 2: Predict the coordination number of Cs+ ion and the structure of CsCl if rcs+ = 1.69 A° and rCl– = 1.81A°
Sol: Given that:
rcs+ = 1.69 A°
rCl– = 1.81A°Radius ration ρ = r+ / r– = 1.69 / 1.81 = 0.9337 A°
As 0.9337 > 0.732, hence the coordination number is 8 and geometry of CsCl is cubic.
Problem 3: Predict the coordination number of Na+ ion and the structure of NaCl crystal if rNa+ = 0.95 A° and rCl– = 1.81A°
Sol: Given that:
rNa+ =0.95A°
rCl– = 1.81A°
Radius ration ρ = r+ / r– = 0.95 / 1.81 = 0.5248 A°
As 0.5248 lies between (0.414 to 0.732), hence the coordination number is 6 and geometry of NaCl is Octahedral.
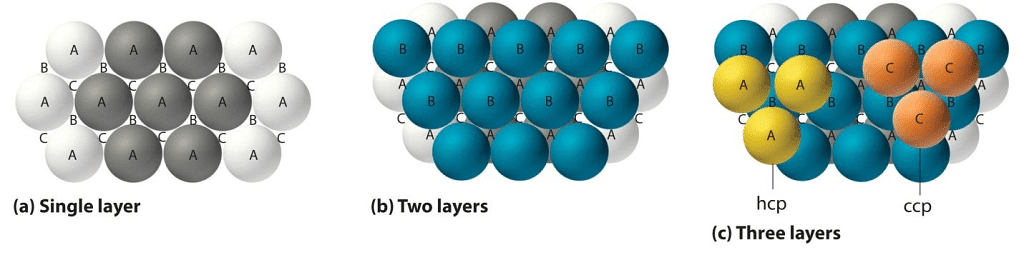
Close Packing of Spheres
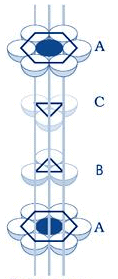
Atoms are space-filling entities and structures can be described as resulting from the packing of spheres. The most efficient, called Closest Packing, can be achieved in two ways, one of which is called Hexagonal Close Packing (Hexagonal Primitive) and the other, Cubic Close Packing (ccp or fcc). Hexagonal close-packing can be built up as follows:Place a sphere on a flat surface. Surround it with six equal spheres as close as possible in the same plane. Looking down on the plane. Let us call this layer as the A layer.
Now form over the first layer a second layer of equally bunched spheres, so as to nestle into the voids. It will be clearly seen that once a sphere is placed over a void, it blocks the void which is adjacent to that void. Let us call this layer as the B layer. Now, it can be clearly seen that there are two types of voids created by the B layer of spheres.
If a sphere is placed on the x - type of voids, it would resemble the A layer of spheres in the sense that it eclipses the spheres of the A layer. This arrangement (i.e., ABAB……) is called the hexagonal close packing (hcp) or hexagonal primitive. On the other hand, if the spheres were to be placed on the y - type of voids, it would neither eclipse the A layer nor the B layer of spheres. This would clearly be a unique layer. Let us call this layer as the C layer. This arrangement (i.e, ABCABC...) is called the Cubic Close Packing (ccp).
 Cubic Closed Packing (ccp)
Cubic Closed Packing (ccp)
Cubic Close Packing
Exercise 1: It can be seen now that both fcc and Hexagonal Primitive Structure have the same packing fraction. Moreover, this is also the highest packing fraction of all the possible unit cells with one type of atom with empty voids. Can you explain this?
Octahedral and Tetrahedral Voids
Sol: The close packing system involves two kinds of voids - tetrahedral voids and octahedral voids. The former has four spheres adjacent to it while the latter has six spheres adjacent to it. These voids are only found in either fcc or Hexagonal Primitive unit cells. Let us first consider an fcc unit cell. Not all the atoms of the unit cell are shown (for convenience). Let us assume that there is an atom (different from the one that forms the fcc) at the center of an edge.
Let it be big enough to touch one of the corner atoms of the fcc. In that case, it can be easily understood that it would also touch six other atoms (as shown) at the same distance. Such voids in an fcc unit cell in which if we place an atom it would be in contact with six spheres at equal distance (in the form of an octahedron) are called octahedral voids.
On calculation, it can be found out that an fcc unit cell has four octahedral voids effectively.
The number of effective octahedral voids in a unit cell is equal to the effective number of atoms in the unit cell.
Let us again consider an fcc unit cell. If we assume that one of its corners is an origin, we can locate a point having coordinates (¼,¼,¼). If we place an atom (different from the ones that form the fcc) at this point and if it is big enough to touch the corner atom, then it would also touch three other atoms which are at the face centers of all those faces which meet at that corner. Moreover, it would touch all these atoms at the corners of a regular tetrahedron. Such voids are called tetrahedral voids.
Since there are eight corners, there are eight tetrahedral voids in a fcc unit cell. We can see the tetrahedral voids in another way. Let us assume that eight cubes of the same size make a bigger cube. Then the centers of these eight small cubes would behave as tetrahedral voids for the bigger cube (if it were face-centered). The number of tetrahedral voids is double the number of octahedral voids. Therefore, the number of tetrahedral voids in hcp is 12.
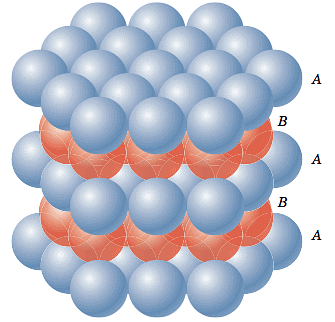 Hexagonal Closed Packing
Hexagonal Closed Packing
Radius Ratio Rules
The structure of many ionic solids can be accounted for by considering the relative sizes of the positive and negative ions, and their relative numbers. Simple geometric calculations allow us to work out, as to how many ions of a given size can be in contact with a smaller ion. Thus, we can predict the coordination number from the relative sizes of the ions.Coordination Number 3
Coordination Number 4 (Tetrahedron)
Coordination Number 6 (Octahedron) or 4 ( Square Planar)
Classification of Ionic Structures
In the following structures, a black circle would denote a cation and a white circle would denote an anion.In any solid of the type AxBy, the ratio of the coordination number of A to that of B would be y: x.
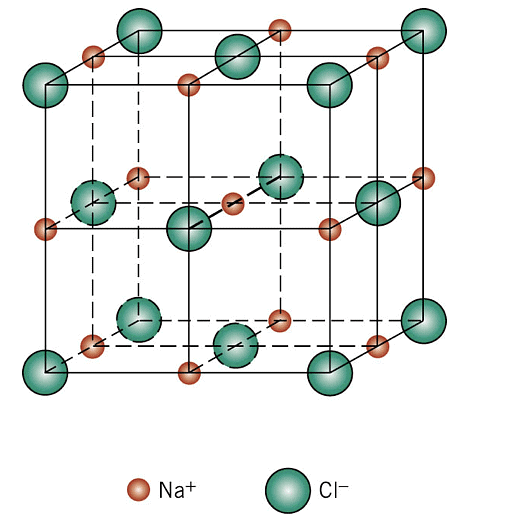
(i) Rock Salt Structure
Cl- is forming an fcc unit cell in which Na+ is in the octahedral voids. The coordination number of Na+ is 6 and therefore that of Cl- would also be 6. Moreover, there are 4 Na+ ions and 4 Cl- ions per unit cell. The formula is Na4Cl4 i.e,NaCl. The other substances having this kind of a structure are halides of all alkali metals except cesium halides and oxides of all alkaline earth metals except beryllium oxide.
(ii) Zinc Blende Structure
Sulfide ions are face centered and Zinc is present in alternate tetrahedral voids. Formula is Zn4S4, i.e, ZnS. Coordination number of Zn is 4 and that of sulfide is also 4. Other substance that exists in this kind of a structure is BeO.
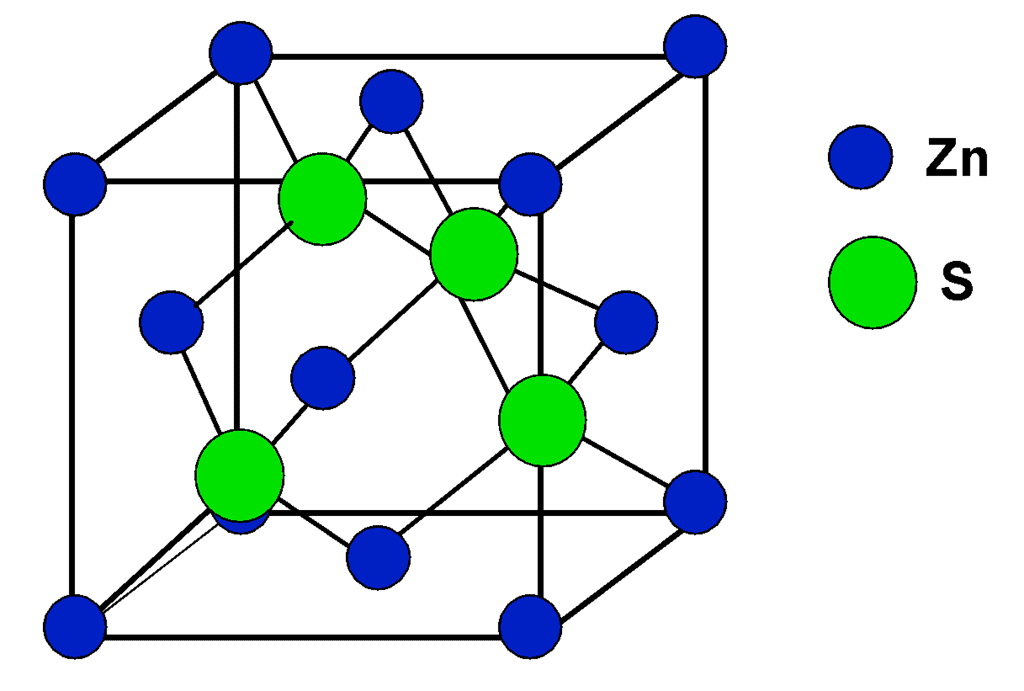
(iii) Fluorite Structures
Calcium ions are face-centered and fluoride ions are present in all the tetrahedral voids. There are four calcium ions and eight fluoride ions per unit cell. Therefore the formula is Ca4F8, (i.e, CaF2). The coordination number of fluoride ions is four (tetrahedral voids) and thus the coordination number of calcium ions is eight. Other substances which exist in this kind of structure are UO2, and ThO2.
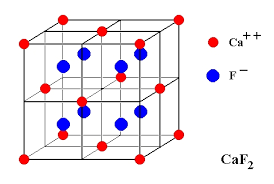
(iv) Anti-Fluorite Structure
Oxide ions are face-centered and lithium ions are present in all the tetrahedral voids. There are four oxide ions and eight lithium ions per unit cell. As it can be seen, this unit cell is just the reverse of Fluorite structure, in the sense that, the positions of cations and anions is interchanged. Other substances which exist in this kind of a structure are Na2O, K2O and Rb2O.

(v) Cesium Halide Structure
Chloride ions are primitive cubic while the cesium ion occupies the center of the unit cell. There is one chloride ion and one cesium ion per unit cell. Therefore the formula is CsCl. The coordination number of cesium is eight and that of chloride ions is also eight. Other substances which exist in this kind of a structure are all halides of cesium.
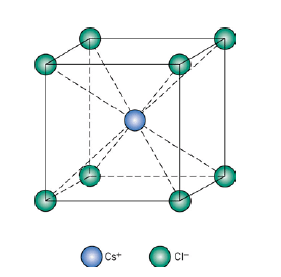
(vi) Perovskite Structure
The general formula is ABO3. One of the cations is bivalent and tetravalent. Example: CaTiO3, BaTiO3. The bivalent ions are present in primitive cubic lattice with oxide ions on the centers of all the six square faces. The tetravalent cation is in the center of the unit cell occupying octahedral void.

(vii) Spinel and Inverse Spinel Structure
Spinel is a mineral (MgAl2O4). Generally they can be represented as M2+M23+O4 , where M2+ is present in one-eighth of tetrahedral voids in a FCC lattice of oxide ions and M3+ ions are present in half of the octahedral voids. M2+ is usually Mg, Fe, Co, Ni, Zn and Mn; M3+ is generally Al, Fe, Mn, Cr and Rh. Examples are ZnAl2O4, Fe3O4, FeCr2O4 etc.
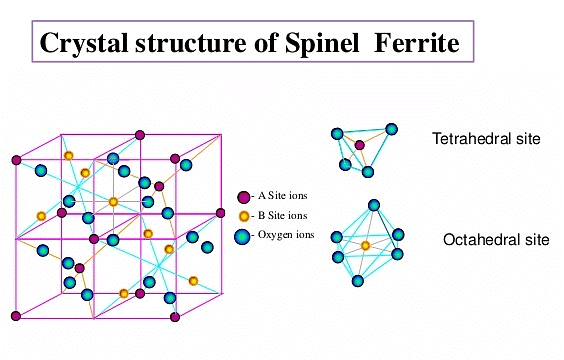
Many substances of the type  also have this structure. In an inverse spinel the ccp is of oxide ions, M2+ is in one-eight of the tetrahedral voids while M3+ would be in one-eight of the tetrahedral voids and one-fourth of the octahedral voids.
also have this structure. In an inverse spinel the ccp is of oxide ions, M2+ is in one-eight of the tetrahedral voids while M3+ would be in one-eight of the tetrahedral voids and one-fourth of the octahedral voids.
Imperfections in a Crystal
The discovery of imperfections in an otherwise ideally perfect crystal is one of the most fascinating aspects of solid state science. An ideally perfect crystal is one which has the same unit cell and contains the same lattice points throughout the crystal.The term imperfection or defect is generally used to describe any deviation of the ideally perfect crystal from the periodic arrangement of its constituents.
Point Defects
Crystalline solids have both short-range and long-range order in how their particles are arranged, but they are not perfect. Usually, a solid is made up of many small crystals, and these small crystals have defects. This occurs when the crystallization process happens quickly or at a moderate rate. Single crystals form when crystallization is extremely slow, but even these are not free from defects. These defects are irregularities in the arrangement of particles. There are two main types of defects: point defects and line defects.
- Point defects are irregularities or deviations from the ideal arrangement around a specific point or atom in the crystal.
- Line defects are irregularities or deviations in entire rows of lattice points.
These irregularities are known as crystal defects. Here, we will focus on point defects only.
Point defects can be classified into three types :
(a) Stoichiometric defects
(b) Impurity defects and
(c) Non-stoichiometric defects.
(a) Stoichiometric Defects
Stoichiometric defects are imperfections in the crystal structure of solids that do not alter the stoichiometric ratio of the compound. These defects can be classified into two main types: vacancy defects and interstitial defects.
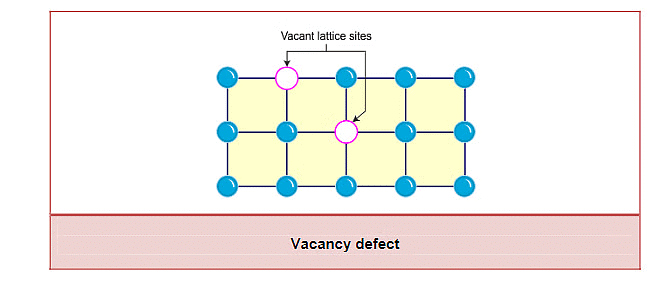
(i) Vacancy Defect
- A vacancy defect occurs when one or more atoms or ions are missing from their regular lattice positions in a crystal.
- The absence of these particles creates empty spaces or "vacancies," which reduce the overall density of the crystal.
- These defects can form naturally during the crystallization process or can be induced by heating the solid, causing atoms to move and leave their positions.
- In a metal crystal like iron (Fe), some iron atoms may be missing from their positions, creating vacancies.
(ii) Interstitial Defect
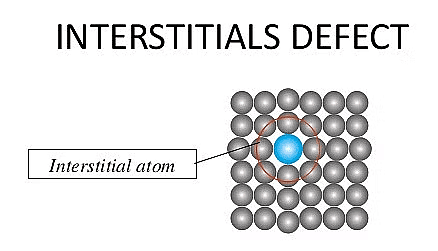
- An interstitial defect occurs when extra atoms or ions occupy positions in the spaces (interstices) between the regular lattice sites of the crystal.
- The addition of these extra particles increases the overall density of the crystal.
- These defects can form when atoms or small molecules get trapped in the interstitial spaces during the crystallization process
- In a metal like steel (an alloy of iron), small carbon atoms can occupy interstitial sites within the iron lattice, creating interstitial defects.
(iii) Schottky Defect
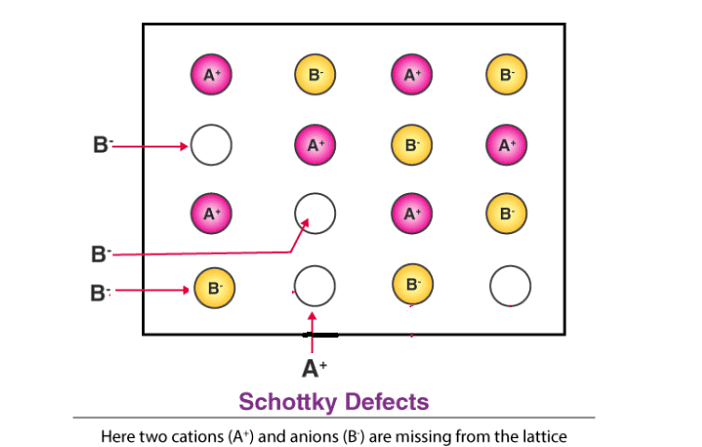
- This is a type of vacancy defect found in ionic solids. To maintain electrical neutrality, equal numbers of cations and anions are missing. Like simple vacancy defects, Schottky defects reduce the density of the solid.
- These defects are significant in number; for example, in NaCl, there are about 10⁶ Schottky pairs per cm³ at room temperature, with approximately 10²² ions per cm³, meaning one Schottky defect per 10¹⁶ ions.
- Schottky defects are seen in ionic substances where the cations and anions are of similar sizes, such as NaCl, KCl, CsCl, and AgBr. Notably, AgBr can exhibit both Frenkel and Schottky defects.
(iv) Frenkel Defect
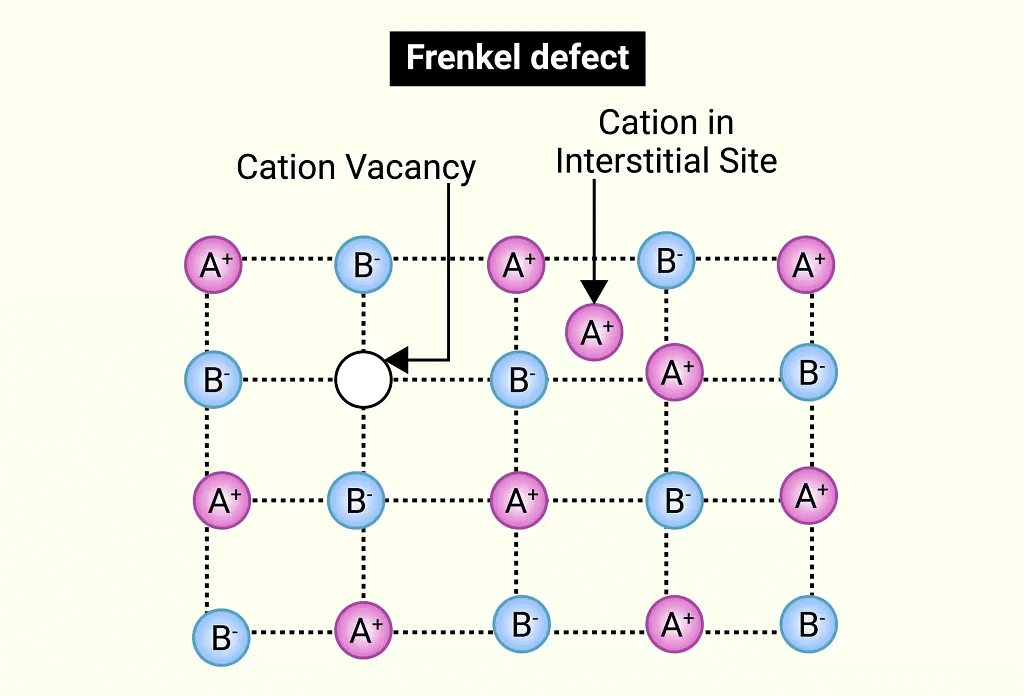
- This defect occurs in ionic solids where a smaller ion (usually a cation) moves from its normal position to an interstitial site, creating both a vacancy at the original site and an interstitial defect at the new location.
- Also known as a dislocation defect, it does not change the overall density of the solid.
- Frenkel defects are common in ionic substances with a large size difference between the ions, such as ZnS, AgCl, AgBr, and AgI, due to the small size of Zn²⁺ and Ag⁺ ions.
(b) Impurity Defects
When molten NaCl containing a small amount of SrCl2 is crystallized, some Na+ ions are replaced by Sr2+ ions . Each Sr2+ ion takes the place of two Na+ ions: it occupies the position of one Na+ ion, leaving the other position vacant. This creates cationic vacancies equal in number to the Sr2+ ions. A similar example is the solid solution of CdCl2 and AgCl.
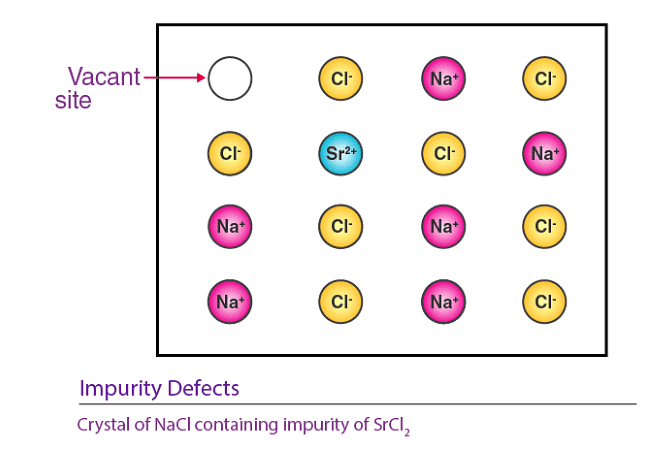
(c) Non - Stoichiometric Defects
The defects mentioned so far do not change the stoichiometry of the crystalline substance. However, many inorganic solids have non-stoichiometric ratios of their constituent elements due to defects in their crystal structures. These defects are of two types: (i) metal excess defect and (ii) metal deficiency defect.
(i) Metal Excess Defect
This defect is of further 2 types -
(a). Metal Excess Defect due to anionic vacancies
Alkali halides like NaCl and KCl exhibit this type of defect. When NaCl crystals are heated in sodium vapor, sodium atoms deposit on the crystal's surface. Chloride (Cl⁻) ions move to the surface and react with sodium atoms to form NaCl, releasing electrons in the process. These electrons diffuse into the crystal and occupy the spots where chloride ions would normally be. This creates an excess of sodium in the crystal. The sites occupied by these unpaired electrons are called F-centers (from the German "Farbenzenter," meaning color center), which give NaCl crystals a yellow color by absorbing visible light. Similarly, excess lithium makes LiCl crystals pink, and excess potassium makes KCl crystals violet (or lilac).
(b). Metal Excess Defect due to anionic vacancies
Zinc oxide (ZnO) is white at room temperature, but turns yellow when heated because it loses oxygen.
The reaction is as follows: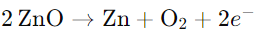
This results in an excess of zinc in the crystal, changing its formula to Zn1+xO. The extra Zn2+ ions occupy interstitial sites, and the electrons move to nearby interstitial sites.
(ii) Metal Deficiency Defect
Many solids are challenging to prepare in their exact stoichiometric composition and often contain less metal than expected. For example, FeO is typically found with a composition of Fe0.95O, but it can range from Fe0.93O to Fe0.96O. In FeO crystals, some Fe2+ cations are missing, and the loss of positive charge is compensated by the presence of the necessary number of Fe3+ ions.
|
108 videos|286 docs|123 tests
|
FAQs on Close Packed Structures, Packing Efficiency & Imperfections in Solids - Chemistry Class 12 - NEET
| 1. What are close packed structures in solids? |  |
| 2. How is the packing efficiency of a crystal lattice calculated? |  |
| 3. What is the radius ratio rule in crystal structures? |  |
| 4. How do imperfections in a crystal lattice affect its properties? |  |
| 5. How does cubic close packing differ from other close packed structures? |  |

|
Explore Courses for NEET exam
|

|