Degree of Freedom | Physical Chemistry for NEET PDF Download
The number of independent variables or coordinates needed to describe the motion of a particle is called the degree of freedom.
- Total number of DOF = 3N (where N = atomicity)
- No. of translational DOF (ft) = 3 (for all gases)
- No. of rotational DOF (fr) = 0 (for monoatomic gas)
No. of rotational DOF (fr) = 2 (for diatomic gas)
No. of rotational DOF (fr) = 2 (for polyatomic linear molecules)
No. of rotational DOF (fr) = 3 (for polyatomic nonlinear molecule) - No. of vibrational dof (fv) = 3N - ft - fr
In a monoatomic species, rotational and vibrational modes of motion are absent. Hence three degrees of freedom corresponds to three translational motion along three different axes.
For a diatomic molecule, total degree of freedom = 3 × 2 = 6
Break up of the Degree of Freedom:
(i) 3 translation degrees of freedom representing translation motion of center of mass in three independent directions. (ii) Two possible axes of rotation, hence two rotational degrees of freedom.
(ii) Two possible axes of rotation, hence two rotational degrees of freedom. (iii) One vibration degree of freedom.
(iii) One vibration degree of freedom.
Vibrational DOF is active only at high temperatures.
Q. Find the total degree of freedom and break up as translational, rotational, or vibrational DOFs in following cases.
(i) O = C = O
(ii)
(iii) He
(iv) NH3
Solution.
(i) CO2: Total dof = 3 x 3 = 9
Translational = 3
Rotational = 2 (∵ linear molecule)
Vibrational = 4
(ii) SO2: Total dof = 3 x 3 = 9
Translational = 3
Rotational = 3 (∵ Bent molecule)
Vibrational = 3
(iii) He: Total dof = 3 (∵ Monoatomic molecule)
Translational = 3
(iv) NH3: Total dof = 3 x 4 = 12
Translational = 3
Rotational = 3 (∵ non linear molecule)
Vibrational = 6
Law of Equipartition of Energy
Energy equal to ½ kT is associated with each translational and rotational degree of freedom per ideal gas molecule.
Energy equal to kT is associated with each vibrational degree of freedom per ideal gas molecule.
Where k = R/NA Boltzmann constant
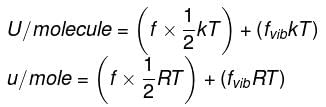
∴ For n moles,
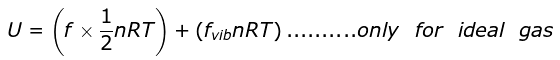
On ignoring vibrational degree of freedom
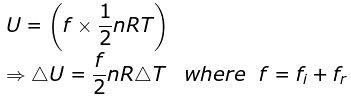
|
117 videos|225 docs|239 tests
|
FAQs on Degree of Freedom - Physical Chemistry for NEET
| 1. What is the Law of Equipartition of Energy? |  |
| 2. How does the Law of Equipartition of Energy relate to temperature? |  |
| 3. What are degrees of freedom in the context of the Law of Equipartition of Energy? |  |
| 4. How does the Law of Equipartition of Energy apply to gases? |  |
| 5. What are the implications of the Law of Equipartition of Energy in different fields of study? |  |






















