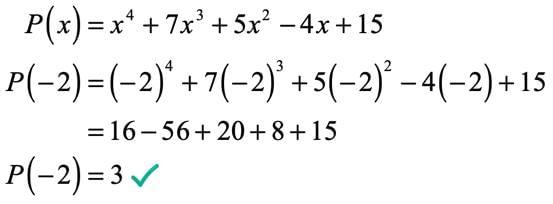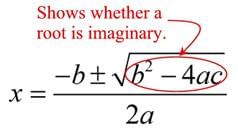|
The degree of a polynomial is defined as the highest power of the variable in the polynomial. |
Card: 2 / 50 |
|
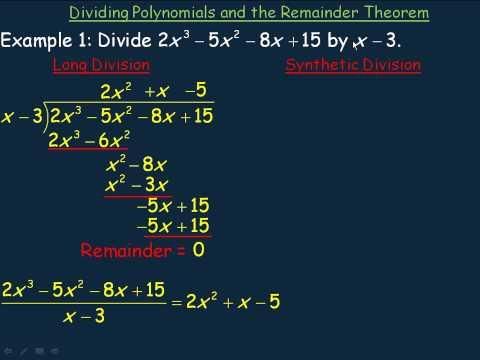
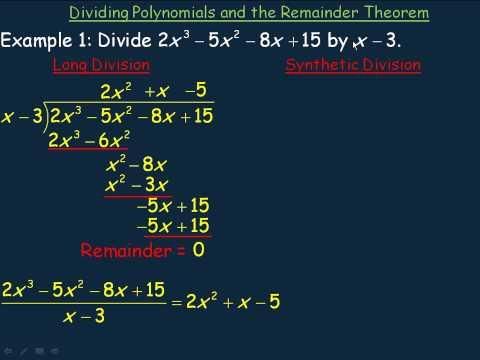
According to the Remainder Theorem, what is the remainder when a polynomial f(x) is divided by (x - a)? |
Card: 21 / 50 |
|
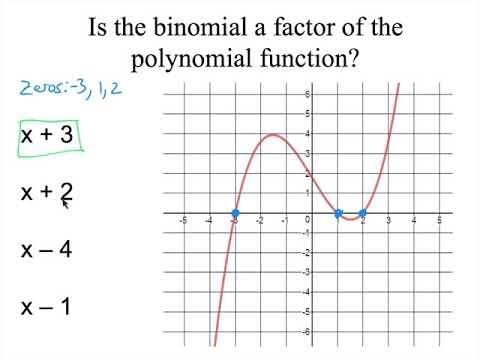
True or False: The Factor Theorem states that if (x - a) is a factor of f(x), then f(a) must be greater than zero. |
Card: 25 / 50 |
 Unlock all Flashcards with EduRev Infinity Plan Starting from @ ₹99 only
|
|
What is the remainder when the polynomial f(x) = x³ - 3x² + x is divided by (x - 1)? |
Card: 27 / 50 |
|
Riddle: I am a polynomial's best friend when it comes to finding factors. What am I? |
Card: 29 / 50 |
|
Fill in the blank: The Remainder Theorem can be used to quickly find the remainder of a polynomial f(x) when divided by ___ . |
Card: 31 / 50 |
|
What is the significance of a remainder of zero when dividing a polynomial by (x - a)? |
Card: 33 / 50 |
|
The general form is ax + b = 0, where 'a' and 'b' are constants and 'a' is not equal to 0.  |
Card: 38 / 50 |
|
Fill in the blank: The discriminant (D) of a quadratic equation determines the nature of the roots. If D < 0,="" the="" roots="" are="" ___="" and="" /> |
Card: 39 / 50 |
|
What is the formula to find the sum and product of the roots of the quadratic equation ax² + bx + c = 0? |
Card: 43 / 50 |
|
The sum of the roots (α + β) is equal to -b/a, and the product of the roots (αβ) is equal to c/a. 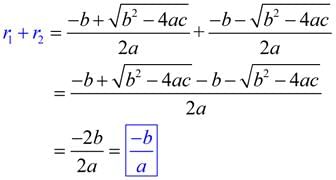 |
Card: 44 / 50 |
|
Fill in the blank: A linear equation with two variables requires ___ equations to uniquely determine the values of both variables. |
Card: 47 / 50 |
|
What determines whether a system of linear equations is consistent or inconsistent? |
Card: 49 / 50 |
|
A system is inconsistent if there are no solutions, and consistent if there is at least one solution, which can be unique or infinite. 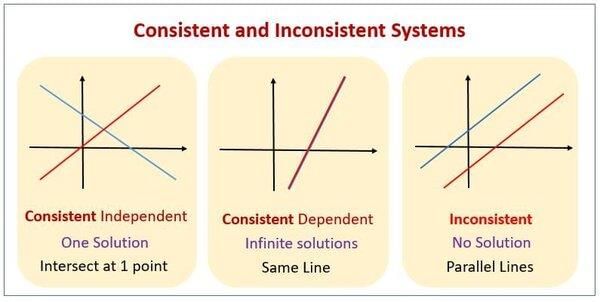 |
Card: 50 / 50 |