Functions from Algebra: Basic Concepts and Application | Quantitative Aptitude (Quant) PDF Download

In real life scenarios , Functions are used to model relationships in business, economics, and analytics. 
For instance, a profit function might relate the quantity of goods sold to total profit, helping in decision-making and forecasting. Understanding functions is essential for analyzing data, optimizing processes and interpreting various business scenarios.

What is a Function?

• In Mathematics and similar areas, a function is a clear connection between two sets. 
•  Each and every item in the first set, known as the domain, is linked to one and only one specific item in the second set, called the codomain. 
• The function is represented as f: X→Y , where X is the Domain, Y is the Codomain and the function is applied to the elements of X to get a unique result in Y.
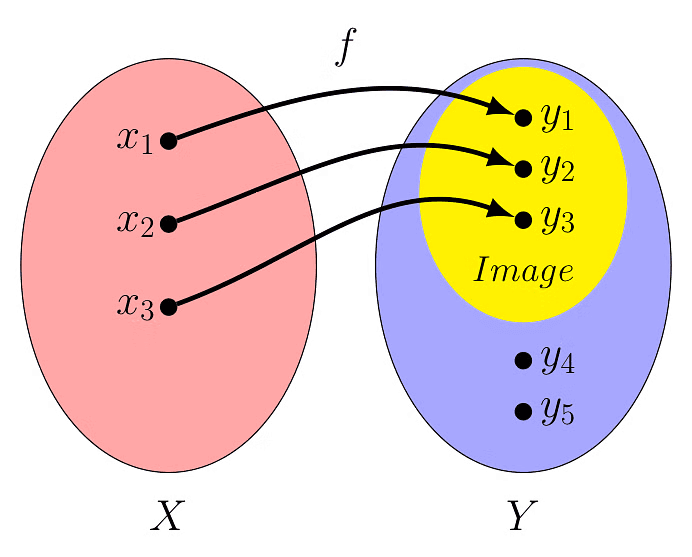
• Here, x_i are called independent variables , y_i are called dependent variables and y_i=f(x_i)

Did You Know: 
Consider two sets X and Y containing 'm' and 'n' elements respectively. 
The number of functions that can be defined from X to Y are  n^m.

Example: How many  functions can be defined from the set X = {1, 2, 3, 4} to set Y={a, b, c}?
a. 81
b. 36
c. 79
d. 24

Sol: The number of Functions that can be defined from X to Y = n^m 
In this Question , Number of elements in set X = 4
Number of elements in set Y = 3
Number of functions from set X to set Y = 3⁴  = 81
Therefore ,the correct answer of the question is 81.           

Basic Methods of Representing Functions

1. Analytical Representation

• In this we represent a function using a formula. 
•  This representation can be the same throughout the domain, such as y = 3x². 
• Or, it can involve different formulas for different sections of the domain, like: y = 3x² when x < 0 and y = x² when x > 0   

2. Graphical Representation

•  This is a very important way to represent functions. 
•  The process involves the x-y plane, where for each value in the domain X of the function, a point P(x ,y) is created. 
•  The abscissa (x-coordinate) of this point is x. 
•  The ordinate (y-coordinate) is found by using a specific value of  x in the function's formula. 
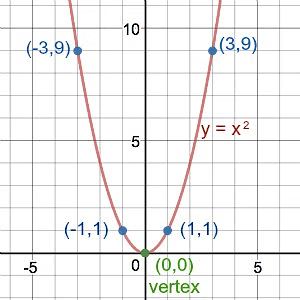
• For example, graphical representation of f(x)= x² with domain, X={-3,-1,1,3} is as follows

3. Tabular Representation

• We show a function using a table.
• First, we list the values of the independent variable x.
• Next, we note the corresponding values of the dependent variable y.
• To find the values of y, we substitute the values of x into the function and mention it in the table.
• For Example, we have a function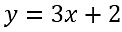, the tabular form for the same with domain X ={-1,0,1,2} is as follows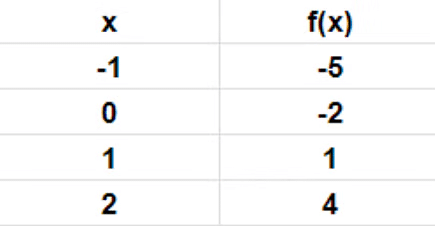

Types of Functions

1. Even Functions

•  Let a function y = f(x)  be given in a certain interval.
• The function is said to be even if for any value of x, f(x) = f(-x)
• Examples of even functions = x ² , x ⁴ , Cos x etc.
  i. x ²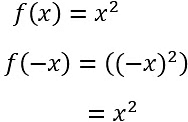
  ii.  x ⁴
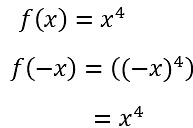  iii. Cos x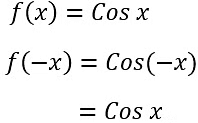
  
  

Properties of Even Function

• The sum, difference, product and quotient of an even function is also even.
  Example, Lets take an example of x ² + x ⁴ + x ⁶
  f(x) = x ² + x ⁴ + x ⁶
  f(-x) = ((-x)²) + ((-x)⁴) + ((-x)⁶)
  = x ² + x ⁴ + x ⁶
• The graph of the even function is symmetrical about the y-axis. 
  In this the symmetry of the graph is across y-axis.
• Graphical Representation
  As we can see in the graph, it is symmetrical about Y-axis. Hence belongs to an Even function.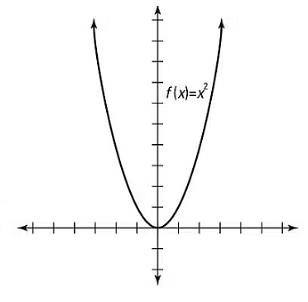
  

Did You Know
In case of Trigonometric functions, only Cos x and Sec x are even functions. 
Rest Trigonometric ratios are odd functions.

 2. Odd Functions

• Let y = f(x)  be the given function in a certain interval.
• The function is said to be odd if for every value of x, f(x)= -f(-x).
• Examples of odd functions = Sin x , x³ etc.  
  i. x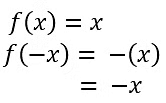  
  ii. x ³
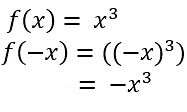  iii. Sin x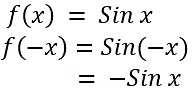
  

Properties of Odd Functions:

• The sum and difference of an odd function is also an odd function.
  Example
  
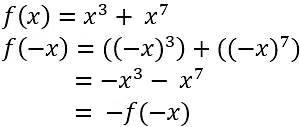
• The product and quotient of an odd function is an odd function.
  Example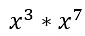
  
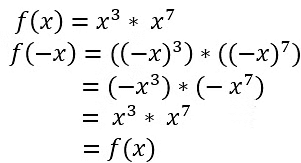
• The graph of the odd function is symmetric about the origin. 
  These graphs have 180-degree symmetry about the origin. 
• Graphical representation:
  The graph given below passes through the origin and is 180-degree symmetric about it. Hence, it belongs to an odd function.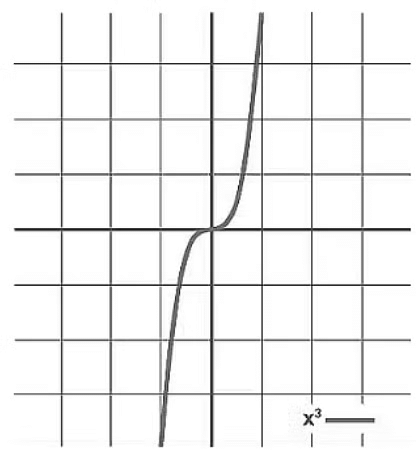
  

Did You Know:

There are certain functions which are Neither Even Nor Odd

• A function is neither even nor odd if it does not exhibit either symmetry about the y-axis or the origin.
• Mathematically, if any function f(x) ≠-f(-x) and f(x) ≠ f(−x) , then the function is said to be neither even nor odd
  Example: Check whether f(x) = x ² + x is an even or an odd function?
  Sol: f(-x) = ((-x)² ) + (-x)
  = x ²- x 
  Which is neither equal to f(x) not equal to f(-x)
  hence, Neither Even nor Odd function.
  

• Graphically, the functions which are Neither Even Nor Odd will neither be symmetric to x-axis or to the origin.
  

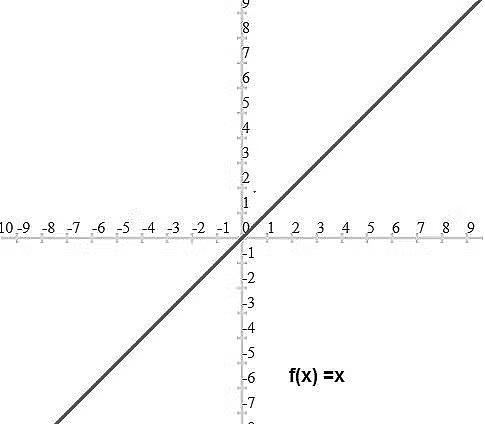
3. Identity Function

•  A function f , defined by f(x) = x for every real number x is known as the identity function. 
•  This function simply means that whatever value you put in, you get the same value out. 
•  In Graphical terms, the identity function is shown as a straight line that passes through the origin at an angle of 45 degrees, indicating that y increases at the same rate as x.
• Graphical Representation,
  

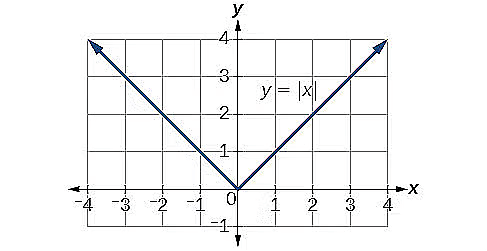
4. Absolute Value Function

• An absolute value function is a function in algebra where the variable is inside the Absolute bars. This function is also known as the Modulus Function and the most commonly used form of the absolute value function is f(x) = |x|
• Mathematically, We represent Absolute Value Function as

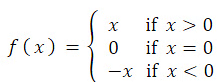
  For example,
  I-3I = -(-3) = 3
  I2I =2
  As we can easily see in the example given above, whatever input we give into a modulus function(whether positive or negative) , it always results in a positive outcome.

• Graphically, 
  

  
  
  

5. Exponential Function

• The function f(x) is defined as f(x) = a^x, where a is a constant that is not equal to 0, and x represents any real number.
• The behavior of the function can change based on the value of a, allowing for either an increasing or decreasing function.

Case-1: If a>1,

For example,
This means y = a^x which demonstrates that the function increases as x gets larger.
The Graphical representation for a>1 is given below,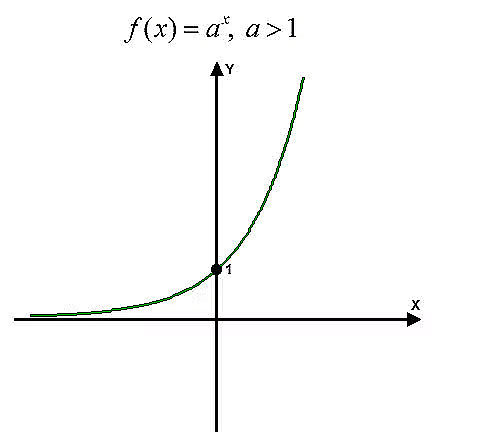

Case-2: If 0<a<1,

• In general, the exponential function decreases as a varies between 0 to 1( 0<a<1).

• The Graphical Representation for 0<a<1 is given below,
  

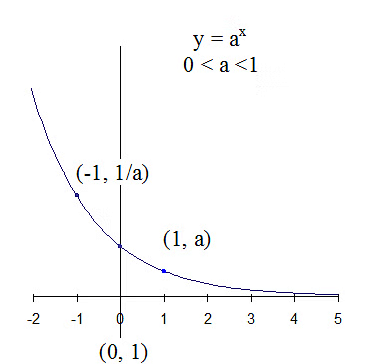
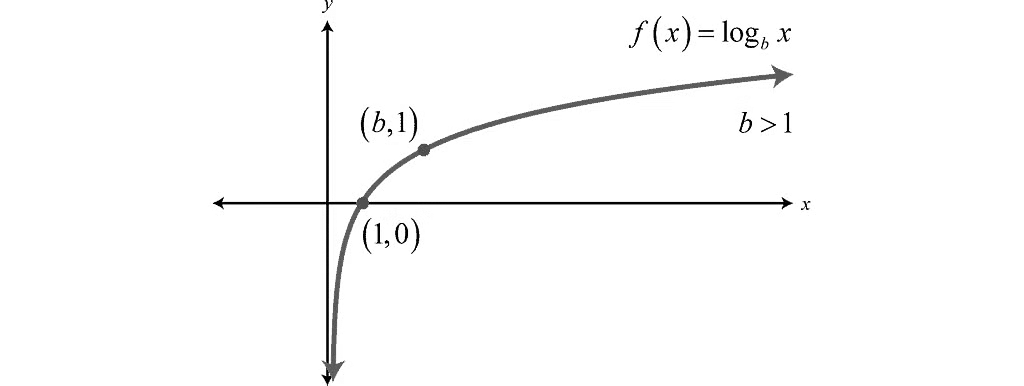
6. Logarithmic Function

• This is an inverse of an exponential function
• The logarithmic function is defined as 

  f(x)=log_ax;(x,a>0)$f\left(x\right)=\log$>0) and a≠0$a\ne 0$.

• The domain of logarithmic function is all positive real number.

• Graphically, we represent logarithmic function as
  

Solved Examples: Types of Functions

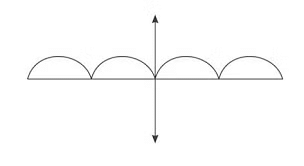
Sol: The graph is symmetrical about the y-axis. 
Hence, graph of an even function.

Example 2: Identify the following graph and explain if it belongs to an Even function or odd function or Neither even nor odd?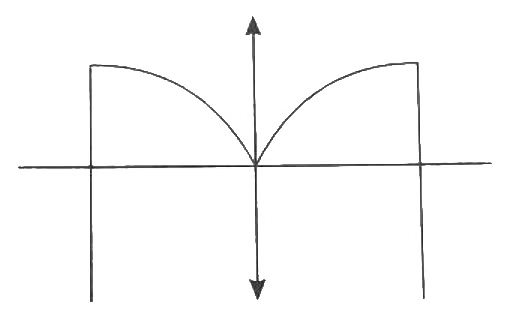

Sol: The graph is symmetrical about the y-axis. 
Hence, graph of an even function.

Example 3: If $f\left(x\right)=x\mathrm{<sup\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; inherit;\; position:\; relative;\; font-size:\; 20px;\; line-height:\; 1.8;\; vertical-align:\; baseline;\; top:\; -0.5em;\; word-break:\; break-word;\; color:\; black;">3</sup>}-2x$ and $g\left(x\right)=3x$, what type of function is $f\left(x\right)+g\left(x\right)$?
a. Even
b. Odd
c. Neither even nor odd
d. None of the above
Ans: Option 'B' is correct.

Sol: $f\left(x\right)$ and $g(x$) are odd functions. 
And as we have learnt from above that the sum of two odd functions is also odd.
therefore  $f\left(x\right)+g\left(x\right)$ is an odd function

Example 4: Identify the following graph and explain if it belongs to an Even function or odd function or Neither even nor odd?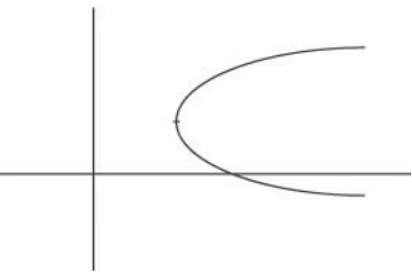

Sol: The graph is neither symmetrical about the y-axis not about origin. 
Therefore, it belongs to Neither Even Nor Odd segment.

Example 5: Identify the following graph and explain if it belongs to an Even function or odd function or Neither even nor odd?

Sol: The graph is symmetrical about origin. 
Therefore , this is the graph of an odd function.

Transformation of Functions

The ability to visualize how graphs shift when the basic analytical expression is changed is a very important skill. 

To understand this concept more precisely, the topic will be further divided into 3 subtopics listen below which are important from various examination point of view like CAT etc.

1. Transformation of Graph from y=f(x)  to y=f(x)±c  (where c represents a positive constant):

• When f(x) is transformed to f(x)+c ,  the graph shifts upward through ‘c’ units.
• For example, The below mentioned graph is of IxI 
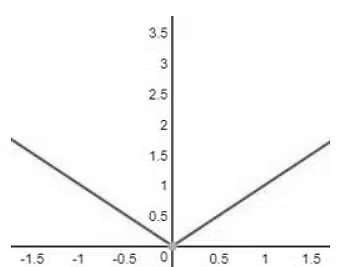  But if we have to plot a graph of IxI+3 , the graph of IxI will move 3 units upward as shown,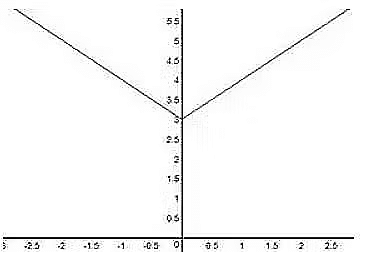
  
• If f(x) is transformed to f(x)-c , the graph shifts downward through ‘c’ units.
• Example We already know the graph of IxI, and if we have to plot the graph of IxI-2, the graph of IxI will shift 2 units downwards as shown below,
  

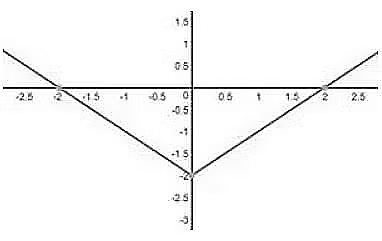
2. Transformation of graph from f(x) to f(x ± c),(where c represents a positive constant):

• When the function f(x) is transformed into f(x +c), the graph shifts through ‘c’ units towards the left. 
• For example, We have to plot a graph of y=Ix+3I,
  
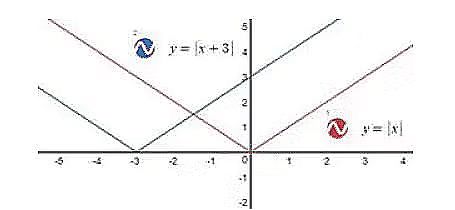
• And when f(x) is transformed into f(x-a), the graph shifts through ‘a’ units towards the right.
• For Example, We have to plot a graph of y=Ix-2I,
  

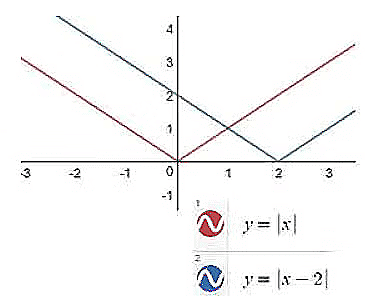
Difference between IxI+a and Ix+aI :
Let us understand the difference between IxI+a and Ix+aI with the following example 
Example : IxI+3 and Ix+3I
1. IxI+3

• This means the absolute value of $x$ plus 3.
• The absolute value $\mid x\mid$ gives the distance of $x$ from 0 on the number line. It is always non-negative (either positive or zero).
• For example:
  Case 1: If $x=2$,
  then $\mid 2\mid +3$
  $=2+3$
  $=5$
  Case 2: If $x=-2$
  then $\mid -2\mid +3$
  $=2+3$
  $=\mathrm{5\; }$
• $\mathrm{<span\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; normal;\; word-break:\; break-word;\; font-size:\; 18px;\; color:\; rgb(0,\; 0,\; 0);\; line-height:\; 1.8;\; font-style:\; normal;\; font-variant-ligatures:\; normal;\; font-variant-caps:\; normal;\; font-weight:\; 400;\; orphans:\; 2;\; text-align:\; left;\; text-indent:\; 0px;\; text-transform:\; none;\; widows:\; 2;\; word-spacing:\; 0px;\; white-space:\; normal;\; background-color:\; rgb(255,\; 255,\; 255);\; text-decoration-thickness:\; initial;\; text-decoration-style:\; initial;\; text-decoration-color:\; initial;\; float:\; none;\; display:\; inline\; !important;">When\; x\; is\; positive,\; IxI+3\; behaves\; like\; y\; =\; x+3</span>}$
• $\mathrm{<span\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; normal;\; word-break:\; break-word;\; font-size:\; 18px;\; color:\; rgb(0,\; 0,\; 0);\; line-height:\; 1.8;\; font-style:\; normal;\; font-variant-ligatures:\; normal;\; font-variant-caps:\; normal;\; font-weight:\; 400;\; orphans:\; 2;\; text-align:\; left;\; text-indent:\; 0px;\; text-transform:\; none;\; widows:\; 2;\; word-spacing:\; 0px;\; white-space:\; normal;\; background-color:\; rgb(255,\; 255,\; 255);\; text-decoration-thickness:\; initial;\; text-decoration-style:\; initial;\; text-decoration-color:\; initial;\; float:\; none;\; display:\; inline\; !important;">When\; x\; is\; negative,IxI+3\; behaves\; like\; y\; =\; -x+3</span>}$

$\mathrm{<span\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; normal;\; word-break:\; break-word;\; font-size:\; 18px;\; color:\; rgb(0,\; 0,\; 0);\; line-height:\; 1.8;\; font-style:\; normal;\; font-variant-ligatures:\; normal;\; font-variant-caps:\; normal;\; font-weight:\; 400;\; orphans:\; 2;\; text-align:\; left;\; text-indent:\; 0px;\; text-transform:\; none;\; widows:\; 2;\; word-spacing:\; 0px;\; white-space:\; normal;\; background-color:\; rgb(255,\; 255,\; 255);\; text-decoration-thickness:\; initial;\; text-decoration-style:\; initial;\; text-decoration-color:\; initial;\; float:\; none;\; display:\; inline\; !important;"><strong\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; normal;\; font-weight:\; 700;\; word-break:\; break-word;\; font-size:\; 20px;\; color:\; black;\; line-height:\; 1.8;\; background-color:\; transparent;\; display:\; inline\; !important;">2.\; Ix+3I</strong></span>}$

• This means the absolute value of $x+3$.
• Here, we first add 3 to $x$ and then take the absolute value of the result. 
• For example: 
  Case 1: If $x=2$, 
  then $\mid 2+3\mid$
  $=\mid 5\mid$
  $=5$
  Case 2: If $x=-4$
  then $\mid -4+3\mid$
  $=\mid -1\mid$
  $=1$
• When $x+3$ is positive (or $x>-3$), it behaves like $y=x+3$
• When $x+3$ is negative (or $x<-3$), it behaves like $y=-(x+3)$
  $=-x-3$

3. Transformation of Graph from f(x) to If(x)I :

• The graph of |f(x)| is drawn by taking the mirror image (in x-axis) of the portion of the graph of f(x) which lies below x-axis.
  
• For example,  if we have to plot a graph of x²-5x+2  , it will be a parabola like mentioned below
  
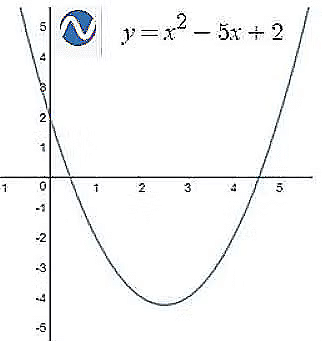
• But if we have to plot a graph of Ix²-5x+2I, then take a mirror image of the portion lying below the x axis. Therefore the graph of Ix²-5x+2I will look like
  

Solved Examples

a) I x²I - 5x
b) x⁴+ x ² 
c) e ^2x+e^-2x
d) x³
Ans: Option 'c' is correct.

Sol: f(x)= e ^2x+e^-2x
f(-x) = e^2(-x)+ e^-2(-x)
= e ^2x+e^{-2x
           = f(x)
Hence, f(-x)=f(x). 
Rest of the options are not even functions as they donot fulfil the  requirement of f(-x)=f(x).}

^{Example 2: Given that x is real and f(x) = f(x + 1) + f(x – 1). Determine the value of ‘a’ that will satisfy f(x) + f(x + a) = 0
a) 2
b) 4
c) 8
d) 3}
Ans:  Option 'd' is correct

Sol: f(x) = f(x + 1) + f(x – 1)
Let f(x) = p and f(x – 1) = q
f(x + 1) = f(x + 1 + 1) + f(x + 1 – 1)                         I(Put x = x + 1 here)
= f(x + 2) + f(x)
p – q = f(x + 2) + p
Or f(x + 2) = -q
f(x + 2) = f(x + 2 + 1) + f(x + 2 – 1)                         I(Put x = x + 2 here)
= f(x + 3) + f(x + 1)
– q = f(x + 3) + p – q
   f(x + 3) = -p
At this point we notice that f(x) = p and f(x+3) = -p
f(x) + f(x + 3) = 0 (This is the condition to be satisfied to determine a)
Hence ‘a’ = 3. 

Example 3: Find the value of x for which x[x] = 39?
a) 7.2
b) 9.2
c) 6.0
d) 6.5

Ans:  Option 'd' is correct.

Sol: When x = 7,
x[x] = 7 * 7 = 49
When x = 6,
x[x] = 6 * 6 = 36
Therefore, x must lie in between 6 and 7 => [x] = 6
=> x = 45[x]$\frac{45}{\left[}$    = 396$\frac{39}{6}$ = 6.5
Hence the answer is 6.5

Example 4: If $f\left(x\right)=x\mathrm{<sup\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; inherit;\; position:\; relative;\; font-size:\; 20px;\; line-height:\; 1.8;\; vertical-align:\; baseline;\; top:\; -0.5em;\; word-break:\; break-word;\; color:\; black;">2</sup>}-4x+3$ , what is the minimum value of $f\left(x\right)$?
a) -1
b) 0
c) 1
d) 3
Ans: Option 'a' is correct.

Sol: $f\left(x\right)=(x-2)\mathrm{<sup\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; inherit;\; position:\; relative;\; font-size:\; 20px;\; line-height:\; 1.8;\; vertical-align:\; baseline;\; top:\; -0.5em;\; word-break:\; break-word;\; color:\; black;">2</sup>}-1$.
The minimum value occurs when $(x-2)\mathrm{<sup\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; inherit;\; position:\; relative;\; font-size:\; 20px;\; line-height:\; 1.8;\; vertical-align:\; baseline;\; top:\; -0.5em;\; word-break:\; break-word;\; color:\; black;">2</sup>}=0$,
giving $f\left(2\right)=-1$
$\mathrm{Therefore\; ,\; x\; =\; 2.}$
f(2)=(2)² -4(2) +3
= -1.

Example 5: If $f\left(x\right)=e\mathrm{<sup\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; inherit;\; position:\; relative;\; font-size:\; 20px;\; line-height:\; 1.8;\; vertical-align:\; baseline;\; top:\; -0.5em;\; word-break:\; break-word;\; color:\; black;">x</sup>}$  is transformed to $g\left(x\right)=e\mathrm{<sup\; style="box-sizing:\; border-box;\; font-family:\; Lato,\; sans-serif;\; letter-spacing:\; inherit;\; position:\; relative;\; font-size:\; 20px;\; line-height:\; 1.8;\; vertical-align:\; baseline;\; top:\; -0.5em;\; word-break:\; break-word;\; color:\; black;">x</sup>}$⁻²+3, describe the transformations.
a) Shifted 2 units left, 3 units up
b) Shifted 2 units right, 3 units up
c)Shifted 2 units left, 3 units down
d) Shifted 2 units right, 3 units down
Ans: Option 'b' is correct.

Sol: There will be the following shifts 

• Horizontal Shift: The $x-2$ inside the exponential function causes a shift 2 units to the right.
• Vertical Shift: The $+3$ outside the exponential function shifts the graph 3 units up.

Application Based Questions

1. Maxima and Minima Based Application

Example:  There were two cat aspirants Ajay and Vijay. Ajay keeps boasting about his quant percentiles( in 90’s).One day Vijay brought a question to Ajay,  it said” There is a function f(x) = ax^2 +bx +c and f(4)= 100 . If the coefficients of a,b and c are distinct positive integers, then find the maximum value ( a+b+c) can attain ? “. 
Can you answer it faster than Ajay? 
a)  82   
b) 76   
c)79   
d) 0
Ans: Option 'a' is correct

Sol:  let us analyze the solution
 F(x) = ax²+bx + c, 
It is given that f(4) = 100   means that by putting x=4, the function will return a value of 100. 
That is f(4)= 16a + 4b + c = 100 , 
Our requirement is to find the maximum value of (a+b+c), so the quantity with the largest coefficient has to be minimized.
 16x1 +4x1 + 80 =100  
 So the maximum value which Ajay got was 1+1+80= 82

2.  Identical Function Based Application

• There is a thumb rule for determining whether the given two functions are identical or not. 
• 'The domain of f(x)  should be equal to the domain of g(x).

Example 1 : Consider two functions, f(x)= ln (x²-5x +6)   and g(x)= ln(x-2) + ln(x-3). Are these functions identical or not?

Sol The ln values cannot be negative or zero .
 So we will analyze both cases.
x² -5x +6x >0 ⇒ (x-2)(x-3)>0 ⇒ x belongs to (-infy,2) U (3,infy)
 (x-2)>0 and (x-3)>0 ⇒  x>2 and x>3 ⇒ x belongs to (2, infy) 
In both cases there are different domains ,so the functions are 'Not Identical'.

Example 2: Consider two functions  f(x)=√x²  and g(x) = |x|. Are these functions identical?

Sol In f(x), for every real value of x , there is a value of f(x), which means x belongs to R.
 In g(x), for every real value of x, there is a value of g(x), which also means x belongs to R.
 In both the cases, the domain is same.
Hence, the functions are 'Identical'

3. Greatest Integer Function Application

• Greatest Integer Function of x, which is mathematically denoted as  [x] indicates the integral part of x which is nearest and smallest integer to x. 
• It is also known as floor of x. 
• Therefore the greatest integer function is simply rounding off the given number to the greatest integer that is less than or equal to the given number.
• Generally,  [x]=n, where n ≤ x < n + 1 and 'n' is an integer.

Example 1:    [9.638]

  Sol   As 9 <9.638 <10
therefore, [9.638] = 9 

Example 2:  [-9.638]

Sol As -10< -9.638 < -9
therefore, [-9.638] = -10

4. Functions In Remainders Based Application

•  The remainder theorem states that If you divide a polynomial f(x) by (x – h), then the remainder is f(h). 
• Therefore, we do not need to use long division,  just need to evaluate the polynomial when x = h to find the remainder.

Example 1: Given that, f(x) = x³ + 2x² – 11x – 12.  Find the remainder if f(x) is divided by (x – 2)?

Sol As we are given that we have to divide f(x) by x-2 and find its remainder
So , The remainder theorem tells us that h = 2, so evaluate f(2) to directly find its remainder without division.
 We replace x with 2 in the polynomial as follows:
 f(2) = 2³ + 2(2)²– 11(2)–12 
f(2) = 8 + 8 – 22 – 12 = -18
Therefore the remainder is -18.

Example 2: The polynomial p(x) satisfies p(−x) = −p(x). When p(x) is divided by x − 3 the remainder is 6. Find the remainder when p(x) is divided by x²− 9.

Sol Now first inference that can be drawn is p(-x)=-p(x) which implies that it is an odd function. 
According to Remainder structure, N = dq+r (N is dividend, d is dividor, q is quotient, r is remainder) 
So ,p(x)=(x-3)*k+6  ((x-3) is dividend, k is divisor, 6 is remainder) 
when p(x) mod x²-9
 p(x)=m*(x²-9)+ax+b (as if the degree of divisor is x² ,then remainder will be of lesser degree i.e ax+b)
 now at x=3
 p(x)=3a+b=6 
and x=-3 remainder will be -6 
p(-3)=-3a+b=-6 
2b=0
so b=0 and a=2 
remainder= ax+b= 2x

5. Function In Quadratics Based Application

Sol Firstly, basics on Quadratic equation , It has only two roots.
One of the root is given to us (i.e 5) which means on substituting the value of 5 in the given f(x) it will result a 0. 
Now, f(x) = ax² +bx+c = 0 
f(2) =  4a +2b +c =0 
f(4)= 16a +4b+c=0 
Using the relation 6 * f(2)= f(4),
24a+12b +6c = 16a+4b+c 
8a+8b+5c=0 
and 25a+5b+c=0; 
we will get a relationship between a and b,  a/b = (- 17/117) 
Let the other root be y 
sum of roots = 5+y = (- b/a) 
solving both the equations,  y = 32 /17

6. Pattern Application of Functions

Sol Since we know both f(0)=1 and f(2)=6, we can find f(1). 
By plugging the value of  x=1 
f(1) = f(0) + f(2) = 7 
f(2) = f(1) + f(3) 
f(3) = f(2) – f(1) 
= 6 – 7 
= −1 
Also, 
f(3) = f(2) + f(4) 
f(4) = f(3) – f(2) 
= −7 
Continuing in a similar way, we can find out 
f(0) = 1 
f(1) = 7 
f(2) = 6 
f(3) = −1 
f(4) = −7 
f(5) = −6 
f(6) = 1 
f(7) = 7 
and so on 
After every 6 integral values of x, f(x) repeats itself. 
f(6) = f(12) = f(18 ) = f(24) = f(30) = f(36) = f(42) = f(48 ) = 1 
f(49) = 7 
f(50) = 6