Irodov Solutions: Constant Electric Field in Vacuum - 3 - NEET PDF Download
Q. 35. Find the electric field strength vector if the potential of this field has the form φ = ar, where a is a constant vector, and r is the radius vector of a point of the field.
Solution. 35. In accordance with the problem 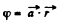
Thus from the equation 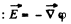
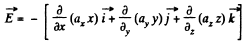
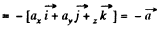
Q. 36. Determine the electric field strength vector if the potential of this field depends on x, y coordinates as
(a) φ = a (x2 — y2);
(b) φ = axy,
where a is a constant. Draw the approximate shape of these fields .using lines of force (in the x, y plane).
Solution. 36. 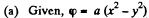
So, 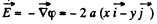
The sought shape of field lines is as shown in the figure (a) of answersheet assuming a > 0:
(b) Since φ = axy
So, 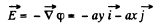
Plot as shown in the figure (b) of answersheet
Q. 37. The potential of a certain electrostatic field has the form cp = a (x2 + y2) + bz2, where a and b are constants. Find the magnitude and direction of the electric field strength vector. What shape have the equipotential surfaces in the following cases:
(a) a > 0, b> 0; (b) a > 0, b < 0?
Solution. 37. 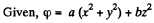
So, 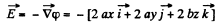
Hence 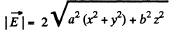
Shape of the equipotential surface :
Put 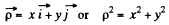
Then the equipotential surface has the equation
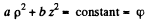
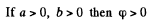 and the equation of the equipotential surface is
and the equation of the equipotential surface is
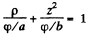
which is an ellipse in p , z coordinates. In three dimensions the surface is an ellipsoid of revolution with semi- axis 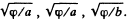
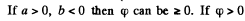 then the equation is
then the equation is
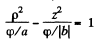
This is a single cavity hyperboloid of revolution about z axis. If φ = 0 then
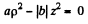
or 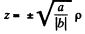
is the equation of a right circular cone.
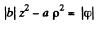
or 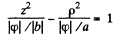
This is a two cavity hyperboloid of revolution about z-axis.
Q. 38. A charge q is uniformly distributed over the volume of a sphere of radius R. Assuming the permittivity to be equal to unity throughout, find the potential
(a) at the centre of the sphere;
(b) inside the sphere as a function of the distance r from its centre.
Solution. 38. From Gauss’ theorem intensity at a point, inside the sphere at a distance r from the centre is given by, 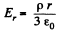 and outside it, is given by
and outside it, is given by 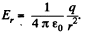
(a) Potential at the centre of the sphere,
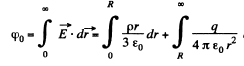
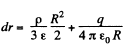
as 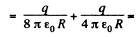
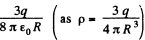
(b) Now, potential at any point, inside the sphere, at a distance r from it s centre.
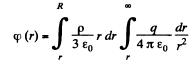
On integration : 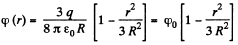
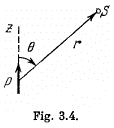
Q. 39. Demonstrate that the potential of the field generated by a dipole with the electric moment p (Fig. 3.4) may be represented as 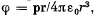 where r is the radius vector. Using this expression, find the magnitude of the electric field strength vector as a function of r and θ.
where r is the radius vector. Using this expression, find the magnitude of the electric field strength vector as a function of r and θ.
Solution. 39. Let two charges +q and - q be separated by a distance l. Then electric potential at a point at distance r > > l from this dipole,
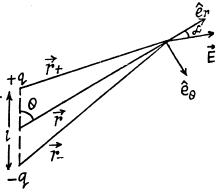
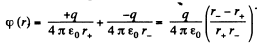 (1)
(1)
But 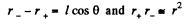
From Eqs. (1) and (2),
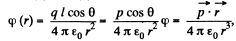
where p is magnitude of electric moment vector.
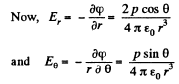
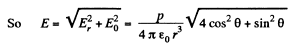
Q. 40. A point dipole with an electric moment p oriented in the positive direction of the z axis is located at the origin of coordinates. Find the projections Ez and E⊥ of the electric field strength vector (on the plane perpendicular to the z axis at the point S (see Fig. 3.4)). At which points is E perpendicular to p?

Solution. 40. From the results, obtained in the previous problem,
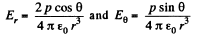
From the given figure, it is clear that,
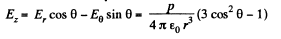
and 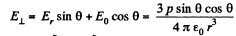
When 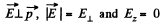
So 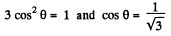
Thus 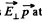 the points located on the lateral surface of the cone, having its axis, coinciding with the direction of z-axis and semi vertex angle
the points located on the lateral surface of the cone, having its axis, coinciding with the direction of z-axis and semi vertex angle 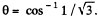
Q. 41. A point electric dipole with a moment p is placed in the external uniform electric field whose strength equals E0, with 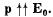 In this case one of the equipotential surfaces enclosing the dipole forms a sphere. Find the radius of this sphere.
In this case one of the equipotential surfaces enclosing the dipole forms a sphere. Find the radius of this sphere.
Solution. 41. Let us assume that the dipole is at the centre of the one equipotential surface which is spherical (Fig.)* On an equipotential surface the net electric field strength along the tangent of it becomes zero. Thus
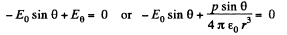
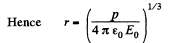
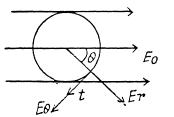
Alternate : Potential at the point, near the dipole is given by,
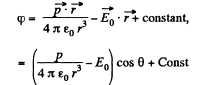
For φ to be constant,
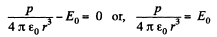
Thus 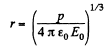
Q. 42. Two thin parallel threads carry a uniform charge with linear densities λ and —λ. The distance between the threads is equal to l. Find the potential of the electric field and the magnitude of its strength vector at the distance r ≫ l at the angle θ to the vector l (Fig. 3.5).
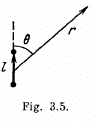
Solution. 42. Let P be a point, at distace r >> l and at an angle to θ the vector 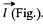
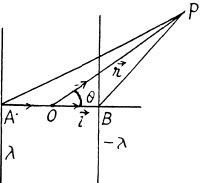
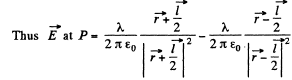
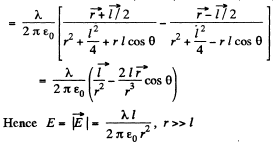
Also, 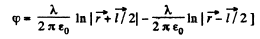
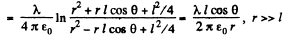
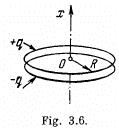
Q. 43. Two coaxial rings, each of radius R, made of thin wire are separated by a small distance l (l ≪ R) and carry the charges q and —q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (Fig. 3.6). Show in the same drawing the approximate plots of the functions obtained. Investigate these functions at |x| ≫ R.
Solution. 43. The potential can be calculated by superposition. Choose the plane of the upper ring as x = l/2 and that of the lower ring as x = - l/2.
Then 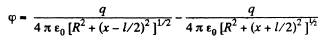
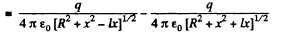
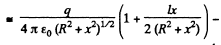
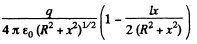
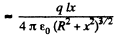
For 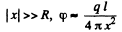
The electric field is 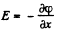
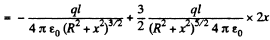
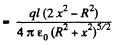
For 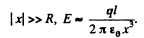 The plot is as given in the book.
The plot is as given in the book.
Q. 44. Two infinite planes separated by a distance l carry a uniform surface charge of densities σ and —σ (Fig. 3.7). The planes have round coaxial holes of radius R, with 1 ≪ R. Taking the origin O and the x coordinate axis as shown in the figure, find the potential of the electric field and the projection of its strength vector Ex on the axes of the system as functions of the x coordinate. Draw the approximate plot φ (x).
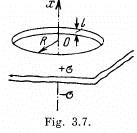
Solution. 44. The field of a pair of oppositely chaiged sheets with holes can by superposition be reduced to that of a pair of uniform opposite charged sheets and discs with opposite charges. Now the charged sheets do not contribute any field outside them. Thus using the result of the previous problem
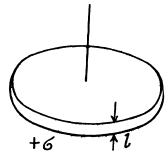
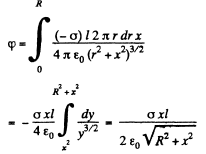
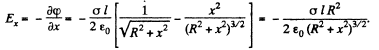
The plot is as shown in the answersheet.
Q. 45. An electric capacitor consists of thin round parallel plates, each of radius R, separated by a distance l (l ≪ R) and uniformly charged with surface densities σ and —σ. Find the potential of the electric field and the magnitude of its strength vector at the axes of the capacitor as functions of a distance x from the plates if x ≫ l. Investigate the obtained expressions at x ≫ R.
Solution. 45. For x > 0 we can use the result as given above and write
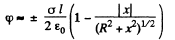
for the solution that vanishes at α. There is a discontinuity in potential for |x| = 0. The solution for negative x is obtained by σ → -σ. Thus
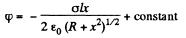
Hence ignoring the jump
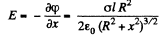
for large 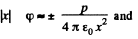
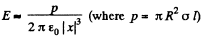
Q. 46. A dipole with an electric moment p is located at a distance r from a long thread charged uniformly with a linear density λ. Find the force F acting on the dipole if the vector p is oriented
(a) along the thread;
(b) along the radius vector r;
(c) at right angles to the thread and the radius vector r.
Solution. 46. 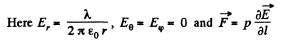
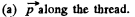
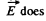 not change as the point of observation is moved along the thread.
not change as the point of observation is moved along the thread.
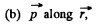
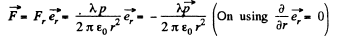
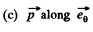
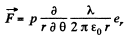
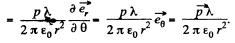
Q. 47. Find the interaction force between two water molecules separated by a distance l = 10 nm if their electric moments are oriented along the same straight line. The moment of each molecule equals p = 0.62.10-29 C • m.
Solution. 47. Force on a dipole of moment p is given by,
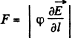
In our problem, field, due to a dipole at a distance l, where a dipole is placed,
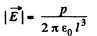
Hence, the force of interaction,
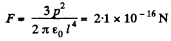
Q. 48. Find the potential φ (x, y) of an electrostatic field E = a (yi xj), where a is a constant, i and j are the unit vectors of the x and y axes.
Solution. 48.
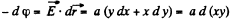
On integrating, 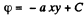
Q. 49. Find the potential φ (x, y) of an electrostatic field E = 2axyi + a (x2 — y2) j, where a is a constant, i and j are the unit vectors of the x and y axes.
Solution. 49.
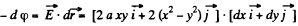
or 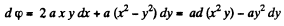
On integrating, we get,
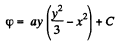
Q. 50. Determine the potential φ (x, y, z) of an electrostatic field E = ayi (ax + bz) j + byk, where a and b are constants, i, j, k are the unit vectors of the axes x, y, z.
Solution. 50. Given, again
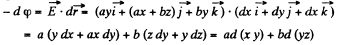
On integrating,
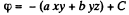
Q. 51. The field potential in a certain region of space depends only on the x coordinate as φ = — ax3 + b, where a and b are constants. Find the distribution of the space charge p (x).
Solution. 51. Field intensity along x-axis.
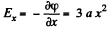 (1)
(1)
Then using Gauss’s theorem in differential from
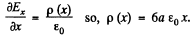
Q. 52. A uniformly distributed space charge fills up the space between two large parallel plates separated by a distance d. The potential difference between the plates is equal to Δφ. At what value of charge density p is the field strength in the vicinity of one of the plates equal to zero? What will then be the field strength near the other plate?
Solution. 52. In the space between the plates we have the Poisson equation
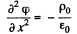
or, 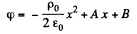
where p0 is the constant space charge density between the plates.
We can choose 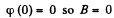
Then 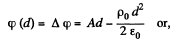
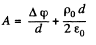
Now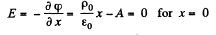
if 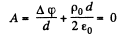
then 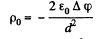
Also 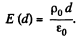
Q. 53. The field potential inside a charged ball depends only on the distance from its centre as φ = ar2 + b, where a and b are constants. Find the space charge distribution p (r) inside the ball.
Solution. 53. Field intensity is along radial line and is
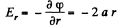 (1)
(1)
From the Gauss’ theorem,
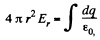
where dq is the charge contained between the sphere of radii r and r + dr.
Hence 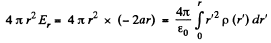 (2)
(2)
Differentiating 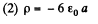
FAQs on Irodov Solutions: Constant Electric Field in Vacuum - 3 - NEET
| 1. What is a constant electric field in vacuum? |  |
| 2. How is a constant electric field created in vacuum? |  |
| 3. What are the applications of constant electric fields in vacuum? |  |
| 4. How does a constant electric field affect charged particles in vacuum? |  |
| 5. Can a constant electric field exist in a medium other than vacuum? |  |














