JEE Advanced (Matrix Match): Complex Numbers | Chapter-wise Tests for JEE Main & Advanced PDF Download
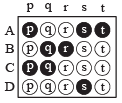
DIRECTIONS (Q. 1 and 2) : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in ColumnII are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example : If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.
Q. 1. z ≠ 0 is a complex number (1992 - 2 Marks)
Column I Column II
(A) Rez = 0 (p) Rez2 = 0
(B) Argz = 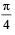 (q) Imz2 = 0
(q) Imz2 = 0
(r) Rez 2 = Imz2
Ans. z ≠ 0 Let z = a + ib Re (z) = 0 ⇒ z = ib
⇒ z2 = – b2
∴ Im (z)2 = 0
∴ (A) corresponds to (q)
Arg 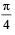 = ⇒ a = b ⇒ z = a + ia
= ⇒ a = b ⇒ z = a + ia
z2 = a2 – a2 + 2ia2 ; z2 = 2ia2 ⇒ Re (z)2 = 0
∴ (B) corresponds to (p).
Q. 2. Match the statements in Column I with those in Column II. (2010) [Note : Here z takes values in the complex plane and Im z and Re z denote , respectively, the imaginary part and the real part of z.]
Column I | Column II |
The set of points z satisfying |z – i| z | | = |z + i | z || is contained in or equal to | (p) an ellipse with eccentricity 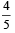 |
(B) The set of points z satisfying |z + 4 | + |z – 4 | = 10 is contained in or equal to | (q) the set of points z satisfying Im z = 0 |
(C) If | w | = 2, then the set of points z = w – 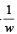 is contained in or equal to is contained in or equal to | (r) the set of points z satisfying |Im z | ≤ 1 |
(D) If | w | = 1, then the set of points z = w + 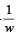 is contained in or equal to is contained in or equal to | (s) the set of points z satisfying | Re z | < 2 |
(t) the set of points z satisfying | z | ≤ 3 |
Ans. 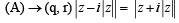
⇒ z is equidistant from two points ( 0, |z|) and (0,– |z|) which lie on imaginary axis.
∴ z must lie on real axis ⇒ Im ( z )=0 also |Im(z)| ≤1
(B) → p
Sum of distances of z from two fined points (–4, 0) and (4, 0) is 10 which is greater than 8.
∴ z traces an ellipse with 2a = 10 and 2ae =8
⇒ e= 4/5
(C) → (p, s, t)
Let ω = 2(cosθ + i sinθ)
then z = ω -  (cosθ + i sinθ) -
(cosθ + i sinθ) - 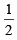 (cosθ + i sinθ)
(cosθ + i sinθ)
⇒ x + iy 
Here 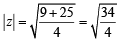
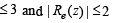
Also x = 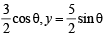 ⇒
⇒ 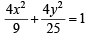
Which is an ellipse with e =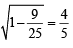
(D) → (q,r, s,t)
Let ω = cosθ + i sinq then z = 2 cosθ ⇒ Imz=0
Also z ≤ 3 and | Im( z) |≤ 1, | Re (z) |≤ 2
DIRECTIONS (Q. 3) : Following question has matching lists. The codes for the list have choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
Q. 3. Let zk = 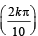 + sin
+ sin 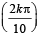 : k=1,2,......,9. (JEE Adv. 2014)
: k=1,2,......,9. (JEE Adv. 2014)
List-I | List-II |
P. For each zk there exists as zj such that zk. zj = 1 | 1. True |
Q. There exists a k ∈ {1, 2,...,9} such that z1.z = zk has no solution z in the set of complex numbers | 2. False |
R. 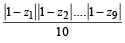 equals equals | 3. 1 |
S. 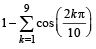 equals equals | 4. 2 |
P Q R S P Q R S
(a) 1 2 4 3 (b) 2 1 3 4
(c) 1 2 3 4 (d) 2 1 4 3
Ans. (c)
(P) → (1) :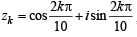 , k = 1 to 9
, k = 1 to 9
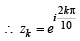
Now zk.zj = 1 ⇒  =
=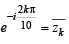
We know if zk is 10th root of unity so will be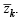
∴ For every zk, there exist zi = 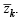
Such that zk . z j = zk.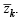 = 1
= 1
Hence the statement is true.
(Q) → (2) z1 =z k ⇒ 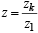 for z1 ≠ 0
for z1 ≠ 0
∴ We can always find a solution to z1.z =zk
Hence the statement is false.
(R) → (3) : We know z10 - 1 = ( z - 1)( z - z1 ) .... ( z-z9 )
⇒ ( z - z1)( z - z2) .... ( z-z9) 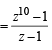
= 1 + z + z2 + ... z9
For z = 1 we get
(1 - z1) (1 - z2) ..... (1 -z9)= 10
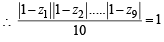
(S) → (4) : 1, Z1, Z2, ... Z9 are 10th roots of unity.
∴ Z10 – 1 = 0
From equation 1 + Z1 + Z2 + .... + Z9 = 0
Re (1) + Re (Z1) + Re (Z2) + .... + Re(Z9) = 0
⇒ Re (Z1) + Re (Z2) + ..... Re(Z9) = – 1
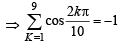
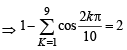
Hence (c) is the correct option.
|
446 docs|930 tests
|
















