JEE Advanced (True/False): Complex Numbers | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q. 1. For complex number z₁ = x₁+ iy₁ and z₂ = x₂+ iy₂ , we write z₁ ∩ z₂ , if x₁ ≤ x₂ and y₁ ≤ y₂ . Then for all complex numbers z with 1 ∩ z , we have    (1981 - 2 Marks)

Ans. T

 Sol. Let z = x + iy

then  1 ∩ z ⇒ 1 ≤ x & 0 ≤ y (by def .)

Consider

 ⇒  

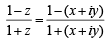
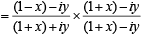
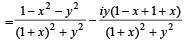
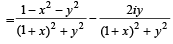
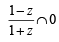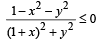
and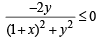  

⇒ 1- x² - y² ≤ 0 and -2y≤0

⇒ x² + y² ≥ 1 and y≥0

which is true as x ≥ 1 &y≥0

∴ The given statement is true ∀ z∈C .
 

Q. 2. If the complex numbers, Z₁, Z₂ and Z₃ represent the vertices of an equilateral triangle such that | Z₁| = | Z₂ | = | Z₃ | then Z₁ + Z₂ + Z₃ = 0. (1984 - 1 Mark)

Ans. T

Sol. As | z₁ | = | z₂ | = | z₃ |
∴ z₁, z₂, z₃ are equidistant from origin.
Hence O is the circumcentre of  ΔABC.

But according to question ΔABC is equilateral and we know that in an equilateral Δ circumcentre and centriod coincide.

∴Centriod of ΔABC = 0

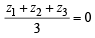⇒     ⇒   z₁ + z₂ +z₃= 0

∴ Statement is true.

Q. 3. If three complex numbers are in A.P. then they lie on a circle in the complex plane. (1985 - 1 Mark) 

Ans. F

Sol. If z₁, z₂, z₃ are in A.P. then,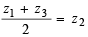

⇒ z₂ is mid pt. of line joining z₁ and z₃.

⇒ z₁, z₂, z₃ lie on a st. line

∴ Given statement is false

Q. 4. The cube roots of unity when represented on Argand diagram form the vertices of an equilateral triangle. (1988 - 1 Mark)

Ans. T

Sol. ∵ Cube roots of unity are 1,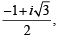  

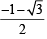
∴ Vertices of triangle are

A(1, 0), B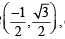 c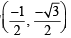

⇒ AB = BC = CA

∴ Δ is equilateral.