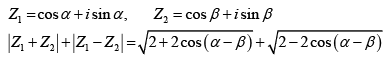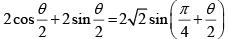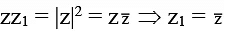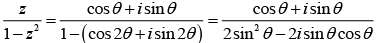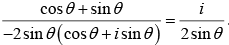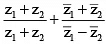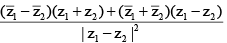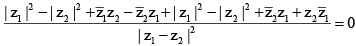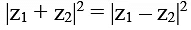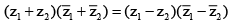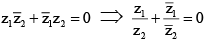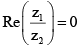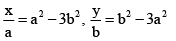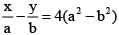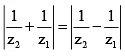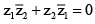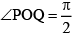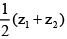JEE Advanced (Single Correct Type): Complex Numbers | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. The value of 1 + i² + i⁴ + i⁶ + … + i²ⁿ is
(a) positive
(b) negative
(c) 0
(d) cannot be evaluated

Correct Answer is option (d)
1 + i² + i⁴ + i⁶ + … + i²ⁿ = 1 – 1 + 1 – 1 + … (–1)ⁿ
This cannot be evaluated unless the value of n is known.

Q.2. If a complex number z lies in the interior or on the boundary of a circle of radius 3 units and centre (– 4, 0), the greatest value of |z +1| is
(a) 4
(b) 6
(c) 3
(d) 10

Correct Answer is option (b)
The distance of the point representing z from the centre of the circle is |z – (-4 + i0)| = |z + 4|
According to the given,
|z + 4| ≤ 3
Now,
|z + 1| = |z + 4 – 3| ≤ |z + 4| + |-3| ≤ 3 + 3 ≤ 6
Hence, the greatest value of |z + 1| is 6.

Q.3. If 1 – i, is a root of the equation x² + ax + b = 0, where a, b ∈ R, then the value of a – b is
(a) -4
(b) 0
(c) 2
(d) 1

Correct Answer is option (a)
Given that 1 – i is the root of x² + ax + b = 0.
Thus, 1 + i is also the root of the given equation since non-real complex roots occur in conjugate pairs.
Sum of roots = −a/1 = (1 – i) + (1 + i)
⇒ a = – 2
Product of roots, b/1 = (1 – i)(1 + i)
b = 1 – i²
b = 1 + 1 {since i² = -1}
⇒ b = 2
Now, a – b = -2 – 2 = -4

Q.4. If [(1 + i)/(1 – i)]^x = 1, then
(a) x = 2n + 1, where n ∈ N
(b) x = 4n, where n ∈ N
(c) x = 2n, where n ∈ N
(d) x = 4n + 1, where n ∈ N

Correct Answer is option (b)
Given,
[(1 + i)/(1 – i)]^x = 1
By rationalising the denominator,
[(1 + i)(1 + i)/ (1 – i)(1 + i)]^x = 1
[(1 + i)²/ (1 – i + i – i²)]^x = 1
[(1 + i² + 2i)/(1 + 1)]^x = 1
[(1 – 1 + 2i)/ 2]^x = 1
i^x = 1
Thus, i^x = i⁴ⁿ, where n is any positive integer.

Q.5. The simplified value of (1 – i)³/(1 – i³) is
(a) 1
(b) -2
(c) -i
(d) 2i

Correct Answer is option (b)
(1 – i)³/(1 – i³)
= (1 – i)³/(1³ – i³)
= (1 – i)³/ [(1 – i)(1 + i + i²)]
= (1 – i)²/(1 + i – 1)
= (1 – i)²/i
= (1 + i² – 2i)/i
= (1 – 1 – 2i)/i
= -2i/i
= -2

Q.6. sin x + i cos 2x and cos x – i sin 2x are conjugate to each other for:
(a) x = nπ
(b) x = [n + (1/2)] (π/2)
(c) x = 0
(d) No value of x

Correct Answer is option (d)
Consider sin x + i cos 2x and cos x – i sin 2x are conjugate to each other.
So, sin x – i cos 2x = cos x – i sin 2x
On comparing real and imaginary parts of both sides, we get
⇒ sin x = cos x and cos 2x = sin 2x
⇒ sin x/cos x = 1 and (cos 2x/sin 2x) = 1
⇒ tan x = 1 and tan 2x = 1
Now, consider tan 2x = 1
Using the formula tan 2A = 2 tan A/(1 – tan²A),
(2 tan x)/(1 – tan²x) = 1
However, this is not possible for tan x = 1.
Therefore, for no value of x, sinx + i cos 2x and cos x – i sin 2x are conjugate to each other

Q.7. If a + ib = c + id, then
(a) a² + c² = 0
(b) b² + c² = 0
(c) b² + d² = 0
(d) a² + b² = c² + d²

Correct Answer is option (d)
Given,
a + ib = c + id
⇒ |a + ib| = |c + id|
⇒ √(a² + b²) = √(c² + d²)
Squaring on both sides, we get;
a² + b² = c² + d²

Q.8. The value of arg (x) when x < 0 is
(a) 0
(b) π/2
(c) π
(d) none of these

Correct Answer is option (c)
Let z = x + 0i and x < 0
Since the point (-x, 0) lies on the negative side of the real axis,
|z| = |x + oi| = √[(-1)² + 0)] = 1
∴ Principal argument (z) = π
Alternative method:
Let x = cos θ + i sin θ
For θ = π, x should be negative.
Thus, x < 0 for θ = π.

Q.9. Number of solutions of the equation z² + |z|² = 0 is
(a) 1
(b) 2
(c) 3
(d) infinitely many

Correct Answer is option (d)
Given,
z² + |z|² = 0, z ≠ 0
⇒ (x + iy)² + [√(x² + y²)]² = 0
⇒ x² – y² + i2xy + x² + y² = 0
⇒ 2x² + i2xy = 0
⇒2x (x + iy) = 0
⇒ x = 0 or x + iy = 0 (not possible)
Therefore, x = 0 and z ≠ 0.
Thus, y can have any real value.
Hence, there exist infinitely many solutions.

Q.10. If the complex number z = x + iy satisfies the condition |z + 1| = 1, then z lies on
(a) x-axis
(b) circle with centre (1, 0) and radius 1
(c) circle with centre (–1, 0) and radius 1
(d) y-axis

Correct Answer is option (c)
Given,
z = x + iy
and
|z + 1| = 1
|x + iy + 1| = 1
⇒ |(x + 1) + iy| = 1
⇒ √[(x +1)² + y²] = 1
Squaring on both sides,
(x + 1)² + y² = 1
This is the equation of a circle with centre (–1, 0) and radius 1.

Q.11. If Z₁, Z₂ are two complex numbers such that |Z₁|= 1, |Z₂| = 1 then the maximum value of |Z₁ + Z₂| + |Z₁ - Z₂| is
(a) 2
(b) 2√2
(c) 4
(d) none of these

Correct Answer is option (b)

Let α - β = θ

Q.12. For complex numbers z₁, z₂ satisfy |z₁| = 12  and  |z₂ – 3 – 4i| = 5, the minimum value of |z₁ – z₂| is
(a) 0
(b) 2
(c) 7
(d) 17 

Correct Answer is option (b)
We know,
| z₁ - z₂ |=| z1 - (z₂ -3- 4i) - 3+ 4i | ≥ | z₁ |- | z₂ - 3- 4i |-| 3+ 4i | ≥ 12 - 5 - 5
(using  | z₁ - z₂ | ≥ | z₁ | - | z₂ | )
∴ | z₁ - z₂ | ≥  2

Q.13. If P(z) and A(z1) two be variable points such that zz₁ = |z|² and 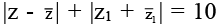 then area enclosed by the curve formed by them
(a) 25p
(b) 20 p
(c) 50
(d) 100 

Correct Answer is option (c)

Now let z = x + iy
⇒ z₁ = x - iy
So,
Which represent a square of area 25.

Q.14. If Z = 1 and Z ≠ 1 , then all the values of  lie on
(a) a line not passing through the origin
(b) Z = √2
(c)The  x - axis
(d) The y – axis

Correct Answer is option (d)
Let z = cosθ + i sinθ
⇒
=
Hence  lies on the imaginary axis i.e. y-axis.

Q.15. If |z₁| and |z₂| are two distinct non-zero complex numbers such that |z₁| = |z₂|, then
(a) purely real
(b) purely imaginary
(c) equal to zero
(d) none of these

Correct Answer is option (b)

=
=
⇒  is purely imaginary.

Q.16. If |z₁ + z₂|² = |z₁ – z₂|² where z₁ and z₂ are non-zero complex numbers, then
(a) Re(z₁/z₂) = 0
(b) Im(z₁/z₂) = 0
(c) Re(z₁ + z₂) = 0
(d) none of these

Correct Answer is option (a)

⇒
⇒

Q.17. If z = x + iy, z^1/3 = a – ib and 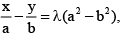 then λ is equal to
(a) 2
(b) 3
(c) 4
(d) 1

Correct Answer is option (c)
z^1/3 = a – ib
⇒ x + iy = (a + i(B)³ = a³ + (-i(B)³ - 3aib(a - i(B)
⇒ x + iy = a³ + ib³ – 3a²bi – 3ab²
⇒  x = a³ – 3ab², y = b³ – 3a²b
⇒
∴

Q.18. The circles x² + y² – 10x + 9 = 0 and x² + y2 = r² intersect each other in two distinct points if
(a) r > 8
(b) r < 2
(c) 7 < r < 11
(d) 1 < r < 9 

Correct Answer is option (d)
C₁ ≡ (5, 0), r1 = 4
C₂ ≡ (0, 0), r₂ = r
(C₁ C₂) = 5
So, r - 4 < 5 < r + 4
⇒ r < q & r > 1
⇒ 1 < r < 9.

Q.19. If P and Q are represented by the  numbers z₁ and z₂ such that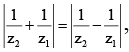  

then the  circumcentre of DOPQ, (where O is the origin) is
(a)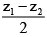
(b)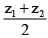
(c)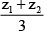
(d) z₁ + z₂ 

Correct Answer is option (b)

⇒ |z₁ + z₂| = |z₁ – z₂|
⇒
z₁/z₂ is purely imaginary
⇒
⇒
⇒ Circumcentre of DPOQ is the mid point of PQ i.e.

Q.20. Let z₁ and z₂ be two complex numbers with α and β as their principal arguments, such that α + β > π , then principal arg( z₁z₂ )is given by
(a) α + β + π
(b) α + β - π
(c) α + β - 2π
(d) α + β

Correct Answer is option (c)
arg (z₁z₂)  = arg (z₁) + arg(z₂) + 2mπ, m ∈ I = α + β - 2π
which should be equivalent to negative angle 7π / 6 - 2π