Kinematic Variables | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Position |

|
| Path Length/Distance |

|
| Displacement |

|
| Average Velocity |

|
| What is Acceleration? |

|
| Acceleration of the Velocity-Time graph |

|
Position
Position can be understood as the location of an object with respect to a reference point. It is expressed as a position vector.
Shown below is the position of a cyclist with respect to a lamp post. Cyclist starts at the lamp post and goes to Position 1, 2, 3 and 4 respectively.
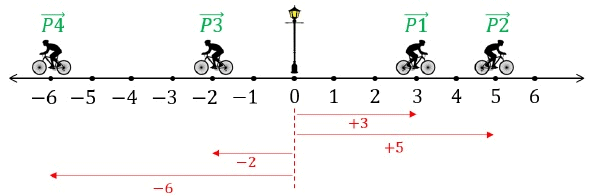
Position 1, P1→ = +3 units
Position 2, P2→ = +5 units
Position 3, P3→ = -2units
Position 4, P4→ = -6units
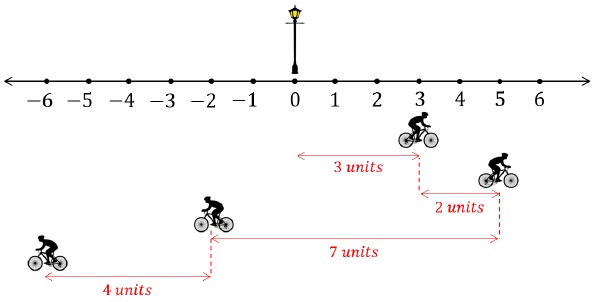
Path Length/Distance
- The total length of the path covered by the moving object.
- It is dependent on the path chosen, thus for motion between two fixed points A and B we can have many different values of the distance traversed.
- It is a scalar quantity, as the length of the path has no indication of the direction in it.
- Its SI unit is meter (m) and its dimension is (L).
- The following image shows the distance covered by the same cyclist.
Displacement
- Shortest distance between the initial and final positions. It is a vector.
- Its magnitude is the minimum distance between the final and initial point and is directed from the initial position to the final position.
- For a particle moving along the x-axis, motion from one position x1 to another position x2, is displacement, Δx where,
Δx = x2 - x1 - If the particle moves from x1= 4m to x2 = 12 m, then Δx = (12m)-(4m) = +8m. The positive result indicates that the motion is in the positive direction. If the particle then returns to x = 4m, the displacement for the full trip is zero. The actual number of meters covered for the full trip is irrelevant, displacement involves only the original and final position.
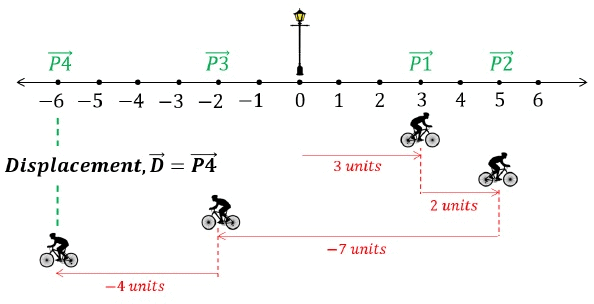 Final Displacement, D→ = -6 units
Final Displacement, D→ = -6 units
It is interesting to observe that the final displacement vector is the same as the final position vector. This is because,
P1→ + P2→ + P3→ + P4→
D→ = 3 + 2 - 7 - 4 = -6 units
General Formula of Displacement
Displacement between two positions starting at PA→ and ending at PB→ is defined as −
Displacement, D→ = PB→ - PA→
For Example, in the figure below,
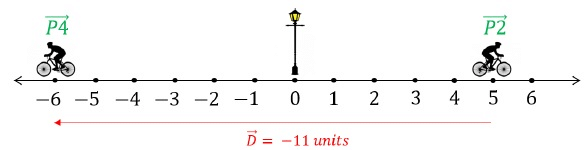
Displacement between position 2 and position 4,
D→ = P4→ - P2→ = -6 - (+5) = -11 units
Distance and Displacement Relationship
The magnitude of Displacement may or may not be equal to Distance.
For example, in the figure below,
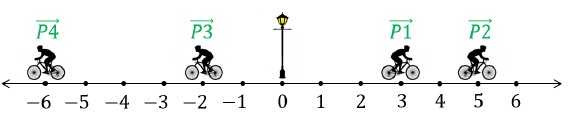
Between P1→ and P2→ −
Distance = 2 units
Magnitude of displacement = |+5 - (+3)| = 2 units
Between P1→ and P3→ −
Distance = 9 units
Magnitude of displacement = |-2 - (+3)| = 5 units
Important Note:
- If the object doesn’t change direction during motion, distance is equal to magnitude of displacement. (as evident between P1→ and P2→)
If the object changes direction during motion, distance is always greater than displacement. (as evident between P1→ and P3→)
Suppose an object is in motion, the position of that object changes with time. But how fast is the position changing with time and in what direction? To understand this, we define average velocity and average speed.
Average Velocity
Average velocity is the ratio of total displacement to total time. Its direction is the same as the direction of the moving object. Even if the object is slowing down, and the magnitude of the velocity is decreasing, its direction would be still the same as the direction in which the object is moving. The magnitude of average velocity is always less than or equal to the average speed because displacement is always smaller than or equal to distance.
It is a vector quantity and has units of m/s
Average velocity = Total Displacement / Total Time
The average velocity of the particle can be positive as well as negative and its positive and negative value depends on the sign of displacement. If the displacement of the particle is zero its average velocity is also zero.
Calculating Average Velocity
The velocity of a particle is: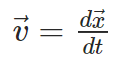
Average Speed
The total distance travelled by the body in total time is the average speed.
Average speed = Total Displacement / Total Time
It is a scalar quantity and its units are m/s.
Calculating Average Speed
Average speed is found by the first finding the total distance covered by the object and dividing it by the total time taken in travelling the distance. Example: A body covers a circle of radius 100m on 100s, implies the total distance covered by him will be d = 2πr = 200π m. So, the average speed will be v = d/t = 2π m/s
If the motion of an object is along a straight line and in the same direction, the magnitude of displacement is equal to the total path length. In that case, the magnitude of the average velocity is equal to the average speed. In case the average speed is not equal to the magnitude of the average velocity, this is because the motion involves a change in direction and so path length is greater than the magnitude of displacement. So the average speed is greater than the magnitude of the velocity.
Solved Examples For You
Q. A particle moves for 20swith velocity 3m/s and then moves with velocity 4m/s for another 20s and finally moves with velocity 5m/s for next 20s what is the average velocity of the particle? (in m/s)
(a) 3
(b) 5
(c) 4
(d) zero
Ans: c
Q.2 An insect crawling straight down the length of a meter stick is at the 12cm mark at one instant, and 22 minutes later is at the 60cm mark. Which one of the following is the magnitude of the insect’s average velocity?
(a) 0.4cm/s
(b) 0.5cm/s
(c) 24cm/s
(d) 30cm/s
Ans: A. The total displacement of insect is S = 60 - 12 = 48cm
Total time taken t = 2min = 120s
Insect’s average velocity = 48/120 = 0.4 cm/s
Instantaneous Speed and Velocity
Let’s carry out a small activity. You are walking towards theatre from home. Suddenly you realize that you are running late and would probably miss the beginning. You start running pretty fast. Maybe it’s been a while since the last time you ran and you slow down a bit. This is ‘instantaneous speed’. And if you include the direction with that speed then you get the instantaneous velocity.
Instantaneous velocity
The rate of change of displacement of an object in a particular direction is its velocity. Its S.I unit is meter per second.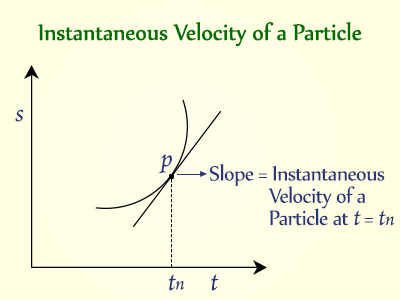

The direction of instantaneous velocity at any time gives the direction of motion of a particle at that point in time. The magnitude of instantaneous velocity equals the instantaneous speed. This happens because, for an infinitesimally small time interval, the motion of a particle can be approximated to be uniform.
Instantaneous Speed
The average velocity tells us how fast an object has been moving over a given time interval but does not tell us how fast it moves at different instants of time during that interval. For this, we define instantaneous speed. It is the rate of change of distance with respect to time.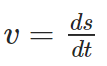 Instantaneous speed is always greater than or equal to zero and is a scalar quantity. For uniform motion, instantaneous speed is constant. To understand it in simple words we can say that instantaneous speed at any given time is the magnitude of instantaneous velocity at that time. It is a limit of the average speed as the time interval become very small.
Instantaneous speed is always greater than or equal to zero and is a scalar quantity. For uniform motion, instantaneous speed is constant. To understand it in simple words we can say that instantaneous speed at any given time is the magnitude of instantaneous velocity at that time. It is a limit of the average speed as the time interval become very small.
A moving object does not have the same speed during its travel. Sometimes it speeds up and sometimes slows down. At a given instant time what we read from the speedometer is instantaneous speed. When a cop pulls you over for speeding, he clocked your car’s instantaneous speed or speed at a specific point in time as your car sped down the road.
Solved Examples For You
Q. Which of the following sentences is an example of instantaneous velocity?
(i) The car covered 500 kilometers first 10 hours of its northward journey.
(ii) Five seconds into launch, the rocket was shooting upward at 5000 meters per second.
(iii) The Cheetah can run at 70 miles per hour.
(iv) Moving at 5 kilometres per hour, it will take us eight hours to get to the base.
(v) Roger Bannister was the first person to run one mile in less than four minutes.
Ans: b
What is Acceleration?
It is the rate of change of velocity with time. The only two ways to accelerate is by changing the speed or change in direction or change both. It is a vector quantity. If the velocity of the object increases with time, its acceleration increases. If the velocity of an object decreases with time, its acceleration is negative.
The motion is uniformly accelerated motion or it non-uniformly accelerated, depending on how the velocity changes with time. It is uniform for a body if the velocity changes by equal amounts in equal intervals and if its velocity changes by unequal amounts, it is non-uniform.

Acceleration= Change in velocity/time taken
Its unit is m/s²
Constant speed does not guarantee that acceleration is zero. For example, a body moving with constant speed in a circle changes its velocity every instant and hence its acceleration is not equal to zero.
Velocity is a quantity having both magnitude and direction, a change in velocity may involve either or both of these factors. Acceleration may result from a change in speed, a change in direction or changes in both. Like velocity, acceleration can also be positive, negative or zero.
Acceleration Formula
Acceleration is a measure of how quickly the velocity of an object changes. So, the acceleration is the change in the velocity, divided by the time. Acceleration has a magnitude (a value) and a direction. The direction of the acceleration does not have to be the same as the direction of the velocity. The units for acceleration are meters per second squared (m/s2).
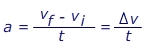
a = acceleration (m/s2)
vf = the final velocity (m/s)
vi = the initial velocity (m/s)
t = the time in which the change occurs (s)
Δv = short form for "the change in" velocity (m/s)
Classification of Motion in Straight Line
Uniform Motion
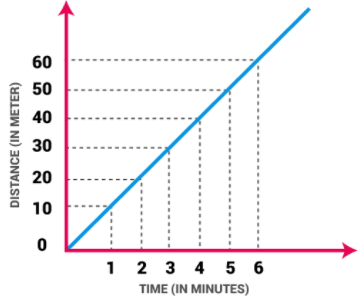
If a body is involved in rectilinear motion and the motion is consistent, then the acceleration of the body must be zero.
Example of Uniform Motion:
(i) If the speed of a car is 10 m/s, it means that the car covers 10 meters in one second. The speed is constant in every second.
(ii) Movement of blades of a ceiling fan.
Non Uniform Motion
This type of motion is defined as the motion of an object in which the object travels with varied speed and it does not cover same distance in equal time intervals, irrespective of the time interval duration.
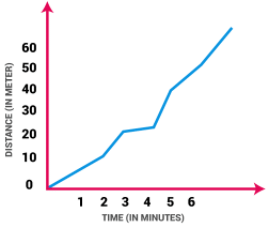
If a body is involved in rectilinear motion, and if the motion is not consistent, then the acceleration of the body must be non-zero.
Example of Non Uniform Motion:
(i) If a car covers 10 meters in first two seconds, and 15 meters in next two seconds.
(ii) The motion of a train.
Now, people usually get confused between uniform motion and uniform acceleration. In the later phenomena, the object is having a constant acceleration in rectilinear motion, which means the object has different speed in every second, which clearly defines that motion is changing.
Motion in Different Acceleration for Different Time Intervals
Let’s understand this through an example. Suppose, a particle started its motion from rest with an acceleration of 1m/s² for 2s and then continued it for next 1s changing to 2m/s². The distance travelled during this will be:
After 2s the velocity is, v = u+at = 2 m/s
Now, if this is the initial velocity for the second half of the motion, s2=ut+(1/2)at² =3 m
Distance traveled in first half is: s1 = 0+(1/2)at² = 2 m
Hence total distance traveled = s1+s2 = 5 m
Average Acceleration
It is the change in velocity divided by an elapsed time. For instance, if the velocity of a marble increases from 0 to 60 cm/s in 3 seconds, its average acceleration would be 20 cm/s². This means that the marble’s velocity will increase by 20 cm/s every second.
It is the rate of change of velocity with respect to displacement
Acceleration is a = dv/dt
∴ a = dv/(dx/v)
a = v(dv/dx)
Freefall object experiences an acceleration of g= 9.8m/s² in a downward direction that is towards the center of the earth. In upward direction it is -g = -9.8m/s²
Acceleration of the Velocity-Time graph
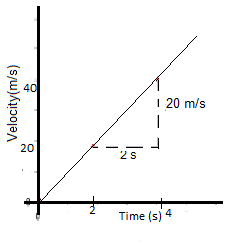
In the given graph, a = (40-20)/(4-2) = 10 m/s2. For a particle it is equal to the slope of a velocity-time graph.
Solved Example:
Q. A stone of mass m is thrown straight upward from the top of a multi-story building with an initial velocity of +15 m/s. Find out the acceleration of stone just after it is thrown?
A. Zero
B. 10m/s² downward
C. 15m/s² upward
D. 15m/s² downward
Answer: B. A body in the air always experiences a gravitational force in a downward direction. Thus the body is in the downward direction with a constant magnitude.
Q. A sports car is travelling at a constant velocity v = 5.00 m/s. The driver steps on the gas, and the car accelerates forward. After 10.0 seconds, the driver stops accelerating and maintains a constant velocity v = 25.0 m/s. What was the car’s acceleration?
Answer: The initial velocity is vi = 5.00 m/s, in the forward direction. The final velocity is vf = 25.0 m/s in the forward direction. The time in which this change occurred is 10.0 s. The acceleration is in the forward direction, with a value:
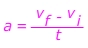
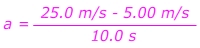

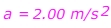
The car's acceleration is 2.00 m/s2, forward.
Q. A child drops a rock off of a cliff. The rock falls for 15.0 s before hitting the ground. The acceleration due to gravity is g = 9.80 m/s2. What was the velocity of the rock the instant before it hit the ground?
Answer: The rock was released from rest, so the initial velocity is vi = 0.00 m/s. The time in which the change occurred is 15.0 s. The acceleration is 9.80 m/s2. The final velocity must be found, so rearrange the equation: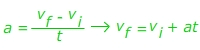
vf = vi + at
vf = 0.00 m/s +(9.80 m/s2)(15.0 s)
vf = 147 m/s
The rock is falling, so the direction of the velocity is down.
|
95 videos|367 docs|98 tests
|
FAQs on Kinematic Variables - Physics Class 11 - NEET
| 1. What is the difference between distance and displacement in kinematics? |  |
| 2. How is average velocity calculated in kinematics? |  |
| 3. What is acceleration in kinematics? |  |
| 4. How can the acceleration of an object be determined from a velocity-time graph? |  |
| 5. What are the key kinematic variables that are commonly used to analyze motion in physics? |  |
















