Linear Programming: Simplex Method | Management Optional Notes for UPSC PDF Download
The simplex method is based on the property that the optimum solution of a L.P. problem if exists can always be found in one of the basic feasible solutions.
Example: Maximise z = x + y, subject to x + y ≤ 5
x + 3y ≤ 12, x ≥ 0, y ≥ 0
Step 1: Convert the inequalities to equalities by addition of non-negative slack variables.
Let s1 and s2 be the slack variables, which convert the inequalities into equations. Then
x + y + s1 =.5 and
3x + 2y +s2 = 10 where s1 ≥ 0 and s2 ≥ 0.
The problem can then be written as follows: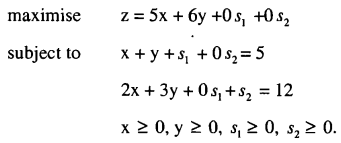
Step 2: Put the problem in a simplex tableau.
The simplex table is given as,
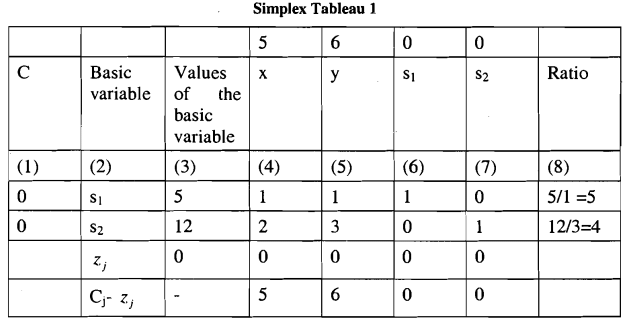
- The first column, denoted by Cj, serves as the objective column, representing the coefficients of the objective function corresponding to the basic variables listed in Column (2). The second column displays the basic variables in the solution. Column (3) showcases the values of these basic variables. Columns (4), (5), (6), and (7) correspond to the variables x, y, S1, and S2 respectively.
- The row under consideration illustrates the coefficients of the respective variables in the objective function and is referred to as the objective row. Column (8) is identified as the ratio column.
- To compute the elements in the Zj row, each entry in the respective column is multiplied by the corresponding value in the objective column (Cj column) and then summed. Conversely, since all the elements in the Cj column are zero, all elements of the Zj row are also zero.
- The difference between the Cj and Zj rows, termed the net evaluation row or index row, is calculated in Step 3. By examining this row, if all elements are zero or negative, the optimal solution is attained. However, the presence of any positive element indicates the potential for formulating a better program, necessitating program revision.
- Determining the pivot column involves identifying the column under which the largest positive element in the net evaluation row is located.
- Find the pivot row and the pivot number: Divide the elements of the constant column by corresponding non-negative elements of the pivot column to form replacement ratio. The row in which the replacement ratio is the smallest is the pivot row. The number lying at the intersection of the pivot row and the pivot column is the pivot number.
- Transform the pivot row: Divide all the elements of the pivot row (starting from the constant column) by the pivot number. The resulting numbers will form the corresponding row of the next table. The non-pivot rows are transformed by using the rule,
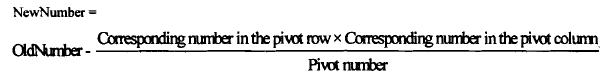
- With the results of (3) and (4) form a new table representing a new basic solution. In the new table the variable of the pivot row of previous table will be replaced by the variable of the column of the previous table.
Then steps 3 and 4 are repeated until an optimal column is reached.
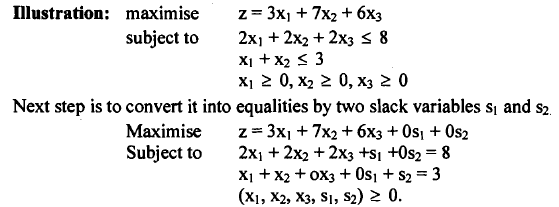
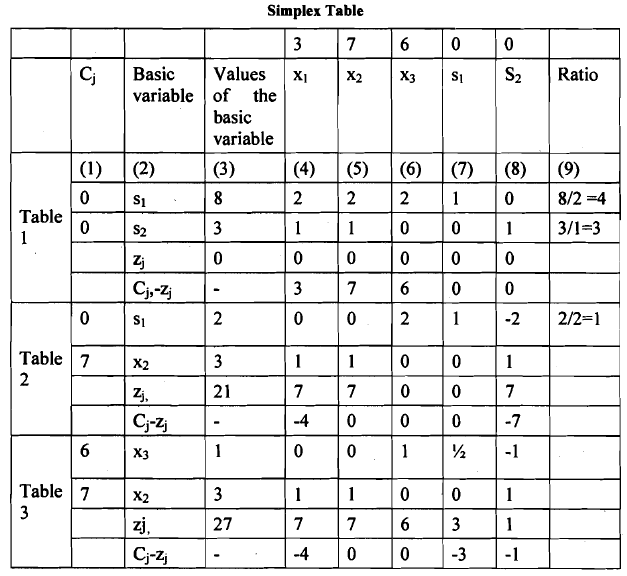
- In the linear programming (LP) program, we incorporate only the slack variables s1 = 8, s2 = 3, x1 = 0, x2 = 0, and x3 = 0. Upon examining this solution, we observe that the objective function's value is zero. Additionally, upon inspecting the Cj-zj row, it becomes evident that there are positive elements present. Consequently, there is potential for formulating an improved program.
- Identifying the highest positive element in the net evaluation row, which is 7 in the x2 column, indicates that the x2 column serves as the pivot column. Therefore, in the subsequent program, x2 needs to be included as one of the basic variables.
- By dividing the elements of the constant column by the non-negative elements of the pivot column, we determine the replacement ratios in column (9). The lowest ratio is identified in the second column (s2), which now becomes the pivot column. As a result, in the next program, s2 will be replaced by x2. The pivot number, denoted as 1, corresponds to the intersection of the pivot row and pivot column.
- The second program is formulated in Table 2, provided below Table 1. In Table 2, the basic variables are s1 and s2. The second row (x2 row) of Table 2 is obtained by dividing the elements of the second row of Table 1 by the pivot number, 1. The elements of the first row (s1 row) of Table 2 are derived following the rule for transforming the non-pivot row. The calculations are outlined below:

- Hence, the second table depicts a basic solution wherein x1 = 0, x2 = 3, x3 = 0, s1 = 2, s2 = 0, and the objective function attains a value of 21. Upon examination of the net evaluation row (Cj-zj), it's evident that one element remains positive. The highest positive number in the net evaluation row is situated in the x3 column, which now serves as the pivot column. Consequently, the variable x3 must be introduced as a basic variable in the subsequent program.
- The smallest replacement ratio in Table 2 is observed in the s1 row. Therefore, this row acts as the pivot row, and in the new program, s1 will be replaced by x3. Hence, the s1 row in Table 2 is designated as the pivot row, with 2 being the pivot number. The third program is illustrated in Table 3, positioned immediately below Table 2.
- By dividing all elements of the s1 row in Table 2 by 2, the pivot number, we obtain the corresponding elements of the first row (x3 row) in Table 3. The elements of the second row (x2 row) in Table 3 are derived from the corresponding elements of the second row (x2 row) in Table 2 by utilizing the rule for transforming non-pivot row(s). These calculations are detailed below:
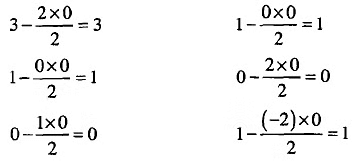
In the third the basic solution is given by X1 = 0, x2 = 3, X3 =1, st — 0, s2 = 0. In the net evaluation row of the table it is found that all the elements are either zero or negative. This means that the optimum program has been attained and there is no scope for further improvement. Hence, the required optimum solution is x1,= 0, x2 = 3 and X3 = 1. The corresponding value of z = 27.
FAQs on Linear Programming: Simplex Method - Management Optional Notes for UPSC
| 1. What is the Simplex Method in linear programming? |  |
| 2. How does the Simplex Method work? |  |
| 3. What are the key steps involved in using the Simplex Method? |  |
| 4. What are the advantages of using the Simplex Method in linear programming? |  |
| 5. Are there any limitations or drawbacks of the Simplex Method? |  |















