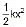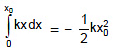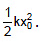Mechanical Energy: Types & Conservation of Mechanical Energy | Physics Class 11 - NEET PDF Download
Mechanical Energy
It is the capacity of an object to do work by the virtue of its motion or configuration (position).
Mechanical Energy is the sum of following two energy terms:
1. Kinetic Energy
It is the ability of an object to do work by the virtue of its motion.
For example, the kinetic energy of Wind has the capacity to rotate the blades of a windmill and hence produce electricity. Kinetic energy is expressed as, where, K is the kinetic energy of the object in joules (J), m is the mass of the object in kilograms and v is the velocity of the object.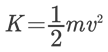
2. Potential energy
It is the ability of an object to do work by the virtue of its configuration or position.
For example, a compressed spring can do work when released. For the purpose of this article, we will focus on the potential energy of an object by the virtue of its position with respect to the earth’s gravity.
Potential energy can be expressed as:
V = m g h
Here,
V is the potential energy of the object in joules (J),
m is the mass of the object in kilograms,
g is the gravitational constant of the earth (9.8 m/s2), and
h is the height of the object from earth’s surface.
Kinetic Energy
Kinetic energy, a fundamental concept in physics, refers to the energy transferred to an object due to its motion.When a force is applied to an object, work is done, leading to a transfer of energy that causes the object to move at a certain speed. This energy associated with the object's motion is called kinetic energy.
How is Kinetic Energy Determined?
Kinetic energy depends on two main factors:
- Mass: The mass of the object.
- Speed: The speed at which the object is moving.
Kinetic Energy (KE) = 1/2 × Mass × Speed²
Key Points About Kinetic Energy:
- Kinetic energy is a scalar quantity, meaning it has only magnitude and no direction.
- It represents the work an object can do because of its motion.
- The greater the mass and speed of an object, the more kinetic energy it has.
Kinetic energy is the energy of motion, determined by the mass and speed of an object. It plays a vital role in various physical phenomena and helps us understand the energy associated with moving objects.

Unit of Kinetic Energy in the SI System
- In the International System of Units (SI), the standard unit for measuring kinetic energy is the Joule (J).
- One Joule is defined as the energy transferred when a force of one newton acts over a distance of one meter. It is mathematically represented as 1 J = 1 kg·m²/s².
- This means that a kinetic energy of one Joule is equivalent to the energy possessed by an object with a mass of one kilogram moving at a velocity of one meter per second.
Example of Kinetic Energy Calculation
To illustrate this concept, consider an object with a mass of 1 kilogram moving at a speed of 1 meter per second.
The kinetic energy (KE) of the object can be calculated using the formula:
KE = 1/2 mv², where m is the mass and v is the velocity.
In this case: KE = 1/2 (1 kg) (1 m/s)² = 0.5 Joules.
This example demonstrates how kinetic energy is quantified in Joules and highlights the relationship between mass, velocity, and energy.

Kinetic Energy Units in the CGS System
- In the CGS system (centimeter-gram-second), the unit of kinetic energy is the erg.
- An erg is defined as the kinetic energy possessed by an object with a mass of 1 gram moving at a velocity of 1 centimeter per second.
- Both the Joule and erg are derived from fundamental units of mass, length, and time.
- This provides a standardized means to express and compare kinetic energy across different measurement systems.
 Comparing Kinetic Energy Units in CGS and SI Systems
Comparing Kinetic Energy Units in CGS and SI Systems
Transformation of Kinetic Energy
- Elastic Collision:
During collisions between objects like billiard balls, kinetic energy can be transferred. When the balls collide and rebound, some of the kinetic energy transforms into other forms, such as heat and sound energy. - Pendulum Swing:
As a pendulum swings back and forth, it continually converts between potential and kinetic energy. At the highest point of the swing, potential energy is dominant, while descending converts potential energy into kinetic energy. - Car Braking:
When a car applies its brakes, the kinetic energy of the moving vehicle transforms into other forms, primarily heat energy. Friction between the brake pads and wheels slows down the car by converting kinetic energy into thermal energy. - Wind Turbine:
In a wind turbine, the kinetic energy of moving air is captured and converted into electrical energy. As the wind blows, it rotates the turbine blades, transforming the wind's kinetic energy into mechanical energy, which then drives a generator to produce electricity. - Waterfall:
As water falls from a higher elevation in a waterfall, its potential energy gradually converts into kinetic energy. Gravity causes the flowing water to gain speed and kinetic energy, which can be harnessed to generate hydroelectric power. - Yo-Yo Transformation:
A yo-yo demonstrates the transformation of kinetic energy. Initially at rest in a person's hand, the yo-yo stores energy as potential energy. When released, gravity pulls the yo-yo downward, converting potential energy into kinetic energy. The yo-yo ball accelerates, gaining speed and kinetic energy. At the bottom of its path, the energy is entirely in the form of kinetic energy.
However, the transformation continues. As the yo-yo reaches the end of its descent, it starts climbing back up due to the tension in the string. The kinetic energy of the yo-yo ball begins converting back into potential energy as it gains height. This process repeats as the yo-yo moves up and down, with continuous conversions between potential and kinetic energy.
Why is Kinetic Energy a Scalar Quantity?
- Kinetic energy is considered a scalar quantity because it does not have an associated direction.
- It represents the magnitude of energy possessed by an object.
- While velocity, which is a vector quantity, includes both magnitude and direction, the calculation of kinetic energy only takes into account the magnitude of velocity.
- The kinetic energy depends on the mass and the square of the magnitude of velocity.
- By squaring the velocity term, kinetic energy is always positive, regardless of the direction of motion.
- Therefore, even though velocity is a vector quantity, the calculation of kinetic energy focuses solely on magnitude, resulting in it being a scalar quantity.
Deriving Kinetic Energy Formula
The formula for calculating kinetic energy is an essential tool in understanding the energy associated with an object’s motion.
The equation for kinetic energy is given by:
KE = 1/2 mv2
To begin, let’s consider a particle of mass m moving with a velocity v. The kinetic energy of this particle can be defined as the work done to accelerate the particle from rest to its current velocity. According to the work-energy theorem, the work done on an object is equal to the change in its kinetic energy.
Work Done on the Particle
The work done on the particle is given by the equation:
- Work = Force x distance
(i) In the case of constant force, the work done can be calculated as:
- Work = Force x distance
Now, let’s express the force in terms of mass and acceleration. According to Newton’s second law of motion, force (F) is equal to mass (m) multiplied by acceleration (a). Since the particle is moving with a constant velocity, its acceleration is zero. Therefore, the force acting on the particle is zero.
Substituting the force into the work equation, we have:
- Work = 0 x displacement
- Work = 0
This means that no work is done on the particle as it moves with a constant velocity. Consequently, there is no change in its kinetic energy.
(ii) In the case when the particle is initially at rest and then accelerated to a final velocity v by an external force.
In this case, work is done on the particle to change its velocity.
The work done on the particle is equal to the change in its kinetic energy. So, we can write:
- Work = Change in kinetic energy
Using the work formula:
- Work = Force x displacement
The force acting on the particle is equal to the mass of the particle (m) multiplied by its acceleration (a). Since the initial velocity is zero, the final velocity is v, and the displacement is d, we have:
- Work = (m x a) x d
Now, recall that the formula for acceleration (a) is given by:
- a = (final velocity - initial velocity) / time
Since the initial velocity is zero, the change in velocity is v and the time taken is t, we can rewrite the equation as:
- a = v / t
Substituting this back into the work equation, we have:
- Work = (m x (v / t)) x d
The quantity (d / t) represents the average velocity (vavg) of the particle. So, we can rewrite the equation as:
- Work = m x (v / t) x d
Now, the average velocity (vavg) is equal to half of the final velocity (v), as the particle starts from rest and reaches a final velocity v. Therefore, we can further simplify the equation as:
- Work = (1/2) m x v x v
Finally, we equate the work done to the change in kinetic energy:
- Work = Change in kinetic energy
Hence, we have derived the equation for kinetic energy:
- K.E = (1/2) m x v²
This equation relates the kinetic energy (K.E) of an object to its mass (m) and velocity (v). It demonstrates that the kinetic energy is directly proportional to the square of the velocity and the mass of the object.
Various Forms of Kinetic Energy
Kinetic energy manifests in different forms depending on the context. Here are some common types:
- Translational Kinetic Energy: This form of kinetic energy pertains to the energy associated with the linear motion of an object. It is most commonly observed when objects move along a straight path.
- Rotational Kinetic Energy: Objects that rotate or spin around an axis exhibit rotational kinetic energy. Examples include spinning tops, wheels, and rotating machinery.
- Vibrational Kinetic Energy: Vibrational kinetic energy arises from the oscillatory motion of particles within a system. It is observed in vibrating strings, molecules, or atoms undergoing vibrational movement.
- Thermal Kinetic Energy: Thermal kinetic energy is linked to the random motion of particles within a substance. It determines temperature and facilitates heat transfer. Higher thermal kinetic energy corresponds to faster particle movement.
- Electrical Kinetic Energy: Electrical kinetic energy is associated with the movement of charged particles, such as electrons, in an electric current. It is employed in various electrical devices and serves as a means of energy transfer.
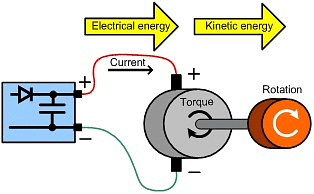
These diverse forms of kinetic energy illustrate the broad range of phenomena where energy is connected to the motion of objects or particles. Each type of kinetic energy possesses distinct characteristics and contributes to different areas of physics and everyday life.
Potential Energy
Potential energy is the energy that an object can store because of its position.
For example, when you pull back a bow, it collects potential energy that becomes kinetic energy when you let go.
A stretched spring also has potential energy, which you can feel as tension when you pull it.
In simple terms, potential energy is a type of energy that comes from changes in an object's position or state.
Potential Energy Formula
The formula for potential energy relies on the specific force acting on the objects. In the case of gravitational force, the formula is as follows:
W = m×g×h = mgh
Where:
- m represents the mass of the object in kilograms
- g denotes the acceleration due to gravity
- h signifies the height of the object in meters
Important points related to Potential energy :
- Potential energy is a simple function that is based solely on position.
- The potential energy of a specific point relies on a reference point.
- The difference in potential energy between two locations does not depend on the frame of reference.
- Potential energy is only defined for conservative forces because the work done by these forces does not vary based on the path taken.
- If we try to define potential energy for non-conservative forces, we would need to calculate the potential energy of a single point using different paths, leading to different values for the same point, which is illogical.
Potential Energy Unit
Gravitational potential energy shares the same units as kinetic energy: kg m²/s².
It's important to note that all forms of energy possess the same units and are measured in joules (J).
Types of Potential Energy
Potential energy manifests in various forms. The two main types are gravitational potential energy and elastic potential energy
Gravitational Potential Energy
Gravitational potential energy refers to the energy possessed by an object that has been raised to a certain height against the force of gravity.
Let's illustrate this with an example:
- Imagine an object with mass (m) placed at height (h) above the ground.
- When the object is raised against gravity, work (W) is done on it.
- According to the law of conservation of energy, the energy gained by the object, in this case, is its potential energy (E).
- Thus, the gravitational potential energy (E) of an object raised to a height (h) above the ground is given by the formula: E = mgh.
- Notably, the distance traveled by the object is not considered; only the displacement between the initial and final heights matters.
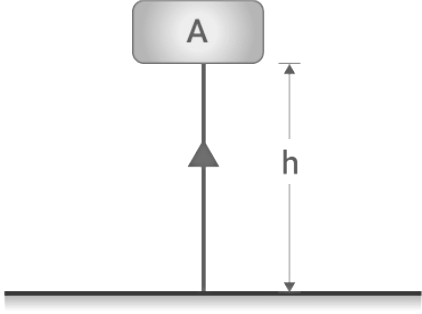
Potential Energy due to height:
- Elastic Potential Energy:
(a) It is a property of stretched or compressed springs.
(b) The end of a stretched elastic spring will begin to move if it is released. The spring. therefore possesses potential energy due to its elasticity. (i.e., due to change in its configuration).
(c) The amount of elastic potential energy stored in a spring of natural length a and spring constant k when it is extended by a length x (from the natural length) is equivalent to the amount of work necessary to produce the extension.
Elastic Potential Energy =
It is never negative whether the spring is extended or compressed. - Proof :


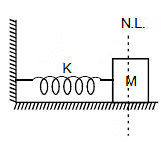
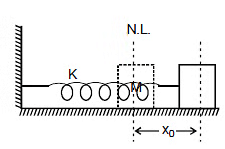
Consider a spring block system as shown in the figure and let us calculate work done by spring when the block is displaced by x0 from the natural length.
At any moment if the elongation in spring is x, then the force on the block by the spring is kx towards left. Therefore, the work done by the spring when block further displaces by dx
dW = - kx dx
Total work done by the spring, W = -

Similarly, work done by the spring when it is given a compression x0 is -

Potential Energy Surfaces
- A potential energy surface (PES) shows the potential energy of a group of atoms based on their positions in space.
- The PES illustrates energy related to one or more coordinates, with a potential energy curve or energy profile representing a PES that focuses on a single coordinate.
- The concept of a landscape is often used to explain this, where different energy values relate to various bond lengths or other important factors.
- Every arrangement of atoms during a chemical reaction corresponds to a specific potential energy, creating a smooth energy landscape.
- This energy landscape allows scientists to study chemistry from a topological viewpoint.
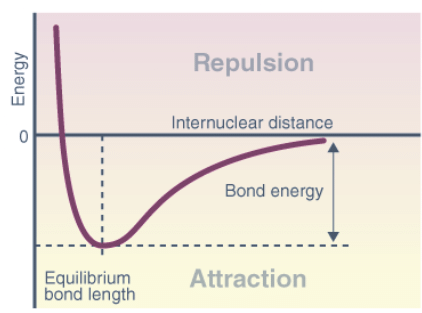
Potential Energy Curves: Understanding 1-D Surfaces
- The potential energy curve (PEC) represents the energy of a molecule as a function of the positions of its nuclei, denoted by r.
- In a system with two atoms, the energy is proportional to their separation. At longer distances, no contact exists, resulting in zero energy.
- As the distance decreases, attractive forces dominate until the atoms reach the minimum point of the curve, where attractive and repulsive forces balance.
- This minimum point determines the bond length or equilibrium bond length, which reflects the average distance at which the atoms oscillate due to thermal motion. Shorter bonds typically indicate stronger bonding.

Analysis of Potential Energy Curves
- Crystal Structure Packing and Bonding Energies: Different atoms arrange themselves in various crystalline formations based on their nature, leading to diverse potential energy curves. Random and dense ordered packing of atoms exhibit contrasting potential energy curves, highlighting the role of crystal structure in determining bonding energies.
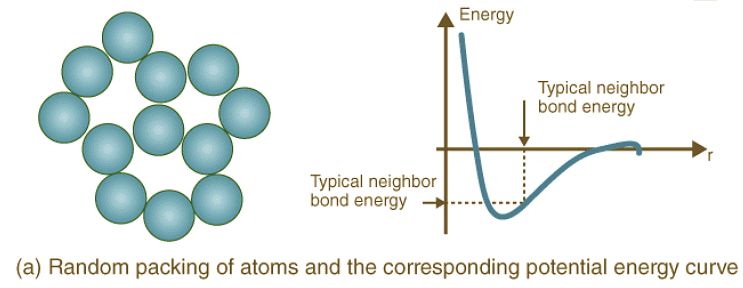
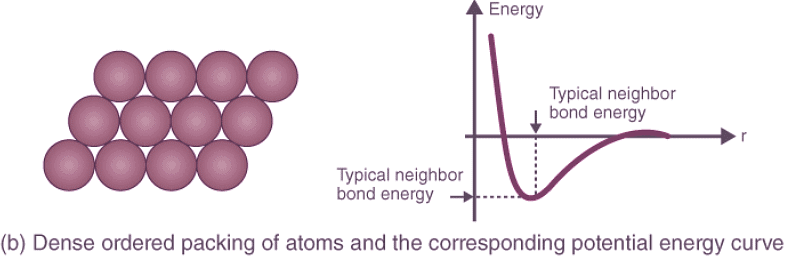
- Mechanical Properties: Mechanical characteristics define how materials deform or break under stress, time, and temperature. Understanding potential energy curves helps elucidate the behavior of materials during deformation, elongation, compression, or fracture.
- Thermal Properties: Heat capacity, thermal expansion, and thermal conductivity describe a material's response to heat. Potential energy curves provide insights into how thermal energy is absorbed and transmitted through atom vibrations in solids.
- Electrical Properties: Electrical conductivity and resistivity characterize a material's ability to conduct electricity. The energy levels and electron availability in potential energy curves influence the electrical properties of solid materials.
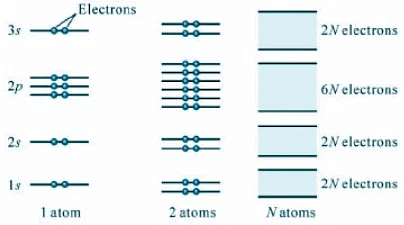
Conclusions
- The potential energy surface and curve are useful tools for studying molecular geometry and the speed of chemical reactions.
- The features of bonding energy and the shape of potential energy curves differ for each material.
- A deep and narrowsection in the curve suggests:
- High bond energy
- High melting temperature
- Large elastic modulus
- Small coefficient of thermal expansion
- The width and asymmetry of the potential energy curve show different properties of materials.
- Various materials have different potential energy curves based on their types of bonding. For example:
- Metals mainly have metallic bonds.
- Polymers have covalent bonds and secondary bonding.
Conservation of Mechanical Energy
- The total mechanical energy of an object at any moment is the sum of its kinetic energy and potential energy.
- According to the law of conservation of energy, "Energy cannot be created or destroyed."
- This means that when a conservative force is acting, the total of an object's kinetic energy and potential energy stays the same.
Before exploring this topic more, let's focus on what a conservative force is.
Proof of Conservation of Mechanical energy
Let us consider the following illustration: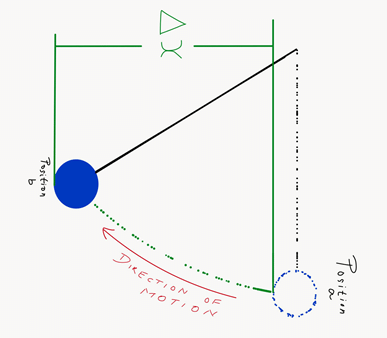
Here, Δx is the displacement of the object under the conservative force F. By applying the work-energy theorem, we have: ΔK = F(x) Δx. Since the force is conservative, the change in potential Energy can be defined as ΔV = – F(x) Δx. Hence,
ΔK + ΔV = 0 or Δ(K + V) = 0
Therefore for every displacement of Δx, the difference between the sums of an object’s kinetic and potential energy is zero. In other words, the sum of an object’s kinetic and potential energies is constant under a conservative force. Hence, the conservation of mechanical energy is proved.
Case Study: Simple Pendulum
The pendulum is a very good example of conservation of mechanical energy. Following illustration will help us understand the pendulum motion: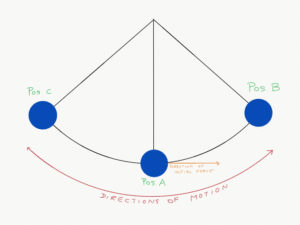
- At position A, Potential energy is zero and the kinetic energy is at maximum.
- When the object travels from position A to B, it’s kinetic energy reduces and potential energy increases.
- At position B, the object stops momentarily. At this position, the object’s kinetic energy becomes zero and its potential energy reaches the maximum. The law of conservation of mechanical energy comes into play here. The object’s entire kinetic energy at position A has been converted to potential energy at position B.
- Now, the object retraces its path, this time from position B to position A. Back at position A, the object’s kinetic energy has been restored to its initial level. Object’s Potential energy is zero.
- Now, the object travels the exact same path as AB, but in reverse direction of AC.
- This process repeats itself infinitely because the mechanical energy of the object remains constant.
This property of mechanical energy has been harnessed by watchmakers for centuries. Of course, in the real world, one has to account the other forces like friction and electromagnetic fields. Hence, no mechanical watch can run perpetually. But, if you get a precise mechanical watch like Rolex, you can expect long power reserves!
Solved Examples For You
Example 1. A mass of 2kg is suspended by a light string of length 10m. It is imparted a horizontal velocity of 50m/s. Calculate the speed of the said mass at point B.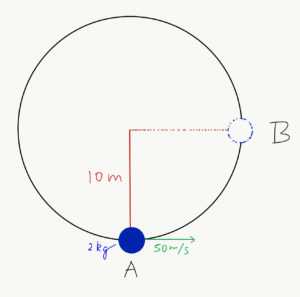
Sol:
Potential energy at point A, V(A) = mgh(A)
Kinetic energy at point A, K(A) = (mv²)/2 = (2 × 2500)/2 = 2500J
Hence, total mechanical energy at point A, K(A) + V(A) = [2500 + V(A)]J
Potential energy at point B, V(B) = mg h(B) = mgh (A + 10) = mg h(A) + 2 × 9.8 × 10
= [V(A) + 196]J
Kinetic energy at point B, K(B) = (mv²)/2
Hence, total mechanical energy at point B, K(B) + V(B) = [K(B) + V(A) + 196]J
By applying the law of conservation of energy,
V(A) + K(A) = V(B) + K(B)
Therefore, V(A) + 2500 = K(B) + V(A) + 196
or K(B) = 2500 – 196
Which gives: (mv²)/2 = 2304
(2 × v²)/2 = 2304
v = [2304]½
Therefore, velocity of the mass at point B = 48m/s
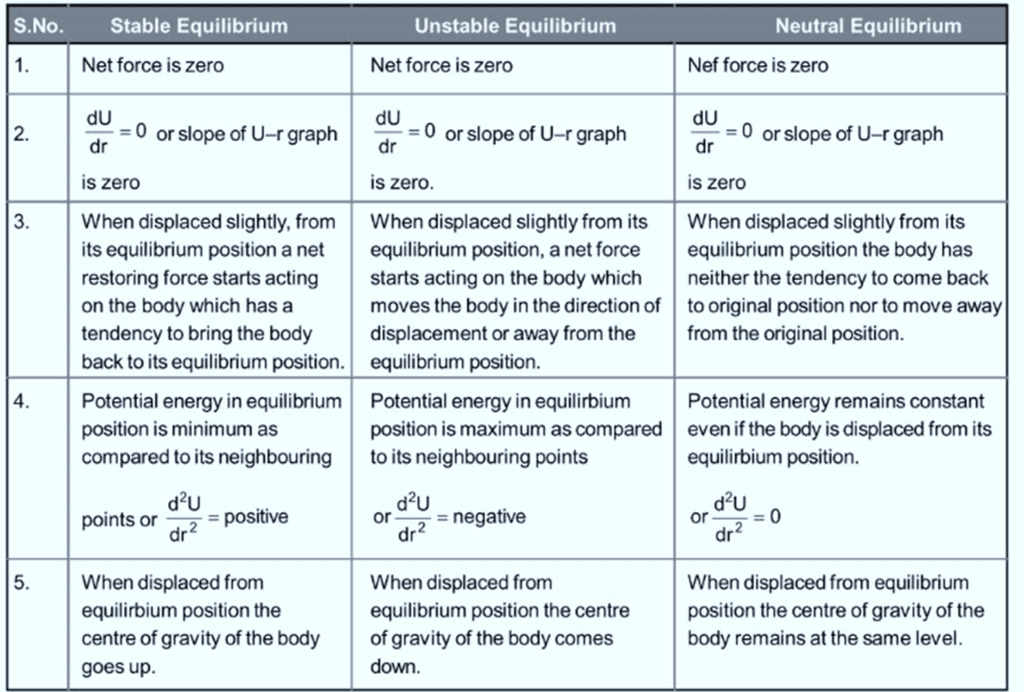
Equilibrium

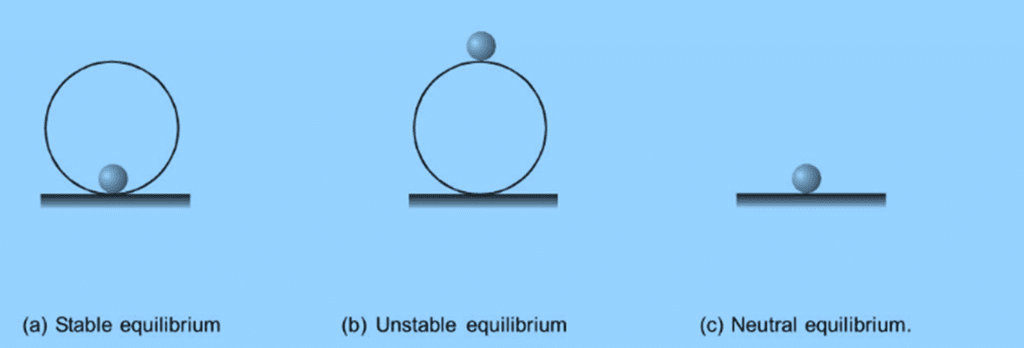
Three identical balls are positioned in equilibrium in different scenarios shown in figures (a), (b), and (c).
(a) A ball is placed inside a smooth spherical shell. This ball is in a position of stable equilibrium.
(b) A ball is positioned on top of a smooth sphere. This ball is in a state of unstable equilibrium.
(c) A ball is on a smooth horizontal surface. This ball is in neutral equilibrium.
Example 5. The potential energy of a conservative system is given by U = ax2 - bx where a and b are positive constants. Find the equilibrium position and discuss whether the equilibrium is stable, unstable or neutral.
Sol:

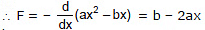
For equilibrium F = 0 or b - 2ax = 0 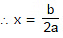
From the given equation we can see that 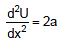 (positive), i.e., U is minimum.
(positive), i.e., U is minimum.
Therefore, 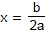 is the stable equilibrium position,
is the stable equilibrium position,
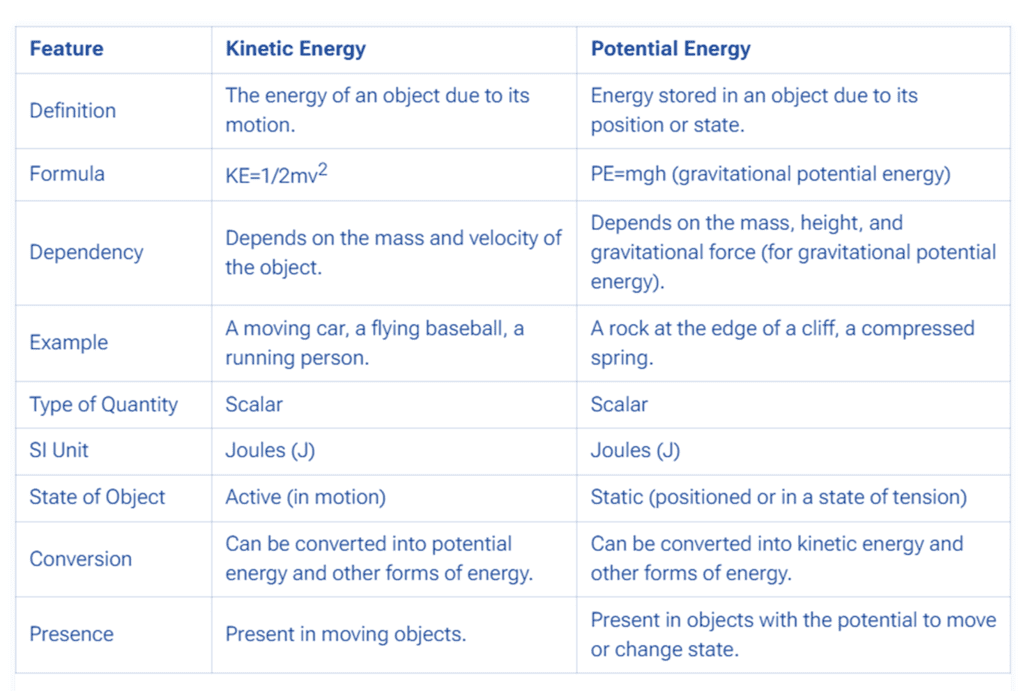
Table to summarise the difference between Kinetic Energy and Potential Energy:
|
97 videos|379 docs|103 tests
|
FAQs on Mechanical Energy: Types & Conservation of Mechanical Energy - Physics Class 11 - NEET
| 1. What is mechanical energy and how is it conserved? |  |
| 2. What are the different forms of kinetic energy? |  |
| 3. What types of potential energy exist and how are they defined? |  |
| 4. How can potential energy surfaces be visualized and analyzed? |  |
| 5. What is the significance of potential energy curves in understanding molecular interactions? |  |