NCERT Exemplar: Oscillations | Physics Class 11 - NEET PDF Download
MULTIPLE CHOICE QUESTIONS I
Q.1. The displacement of a particle is represented by the equation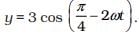
The motion of the particle is
(a) Simple harmonic with period 2p/w.
(b) Simple harmonic with period π/ω.
(c) Periodic but not simple harmonic.
(d) Non-periodic.
Ans. (b)
Solution.
- Acceleration is always directed towards the man position and so is always opposite to displacement, i.e. a ∝ -y or a = -ω2y
- The differential equation of S.H.M is
 and the solution of this differential equation is y = a cos(ωt + φ0)
and the solution of this differential equation is y = a cos(ωt + φ0)
Method 1: The displacement of the particle y = 3 cos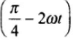
Velocity of the particle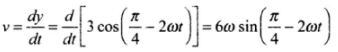
Acceleration 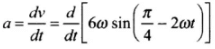
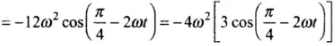
Hence a = -4ω2y = -(2ω)2y
It means acceleration, a ∝ -y, the motion is SHM.
Hence angular frequency of S.H.M, ω' = 2ω
It means the motion is SHM with period π/ω.
Method 2: Given the equation of displacement of the particle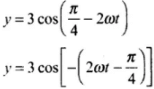
We know cos(-θ) = cosθ
Hence y = 3cos ...(i)
...(i)
Comparing with y = a cos(ωt + ϕ0)
Hence (i) represents simple harmonic motion with angular frequency 2ω.
Hence its time period, 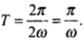
Q.2. The displacement of a particle is represented by the equation y = sin3ωt. The motion is
(a) Non-periodic.
(b) Periodic but not simple harmonic.
(c) Simple harmonic with period 2π/ω.
(d) Simple harmonic with period π/ω.
Ans. (b)
Solution.
There are certain motions that are repeated at equal intervals of time. Let the the interval of time in which motion is repeated. Then x(t) =x(t + T), where T is the minimum change in time. The function that repeats itself is known as a periodic function.
Given the equation of displacement of the particle, y = sin3ωt
We know sin 3θ = 3 sin θ - 4 sin3θ
Hence 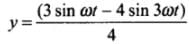
⇒ 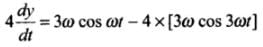
⇒ 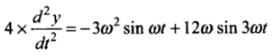
⇒ 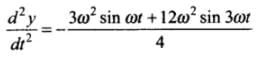
⇒ d2y/dt2 is not proportional to y.
Hence, motion is not SHM.
As the expression is involving sine function, hence it will be periodic.
Also sin3ωt = (sin ωt)3
= [sin(ωt + 2π)]3 = [sinω(t + 2π/ω)]3
Hence, y = sin3ωt represents a periodic motion with period 2π/ω.
Q.3. The relation between acceleration and displacement of four particles are given below:
(a) ax = + 2x.
(b) ax = + 2x2.
(c) ax = – 2x2.
(d) ax = – 2x.
Which one of the particles is executing simple harmonic motion?
Ans. (d)
Solution.
In case of simple harmonic motion, the acceleration is always directed towards the mean position and so is always opposite to displacement, i.e. a α = -x or a = -ω2x
In option (d) ax = -2x or a α -x, the acceleration of the particle is proportional to negative of displacement.
Hence it represents S.H.M.
Q.4. Motion of an oscillating liquid column in a U-tube is
(a) Periodic but not simple harmonic.
(b) Non-periodic.
(c) Simple harmonic and time period is independent of the density of the liquid.
(d) Simple harmonic and time-period is directly proportional to the density of the liquid.
Ans. (c)
Solution.
If the liquid in U-tube is filled to a height h and cross¬section of the tube is uniform and the liquid is incompressible and non- viscous. Initially the level of liquid in the two limbs will be at the same height equal to h. If the liquid is-pressed by y in one limb, it will rise by y along the length of the tube in the other limb, so the restoring force will be developed by hydrostatic pressure difference
Restoring force F = Weight of liquid column of height 2y
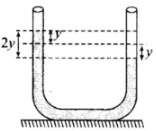
⇒ F = -(A x 2y x ρ) x g = -2Aρgy
⇒ F ∝ -y
Motion is SHM with force constant
k = 2Aρg
⇒ Timeperiod T = 
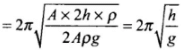
which is independent of the density of the liquid.
Q.5. A particle is acted simultaneously by mutually perpendicular simple hormonic motions x = a cos ωt and y = a sin ωt . The trajectory of motion of the particle will be
(a) An ellipse.
(b) A parabola.
(c) A circle.
(d) A straight line.
Ans. (c)
Solution.
If two S.H.M’s act in perpendicular directions, then their resultant motion is in the form of a straight line or a circle or a parabola etc. depending on the frequency ratio of the two S.H.Ms and initial phase difference. These figures are called Lissajous figures.
Let the equations of two mutually perpendicular S.H.M’s of same frequency be
x = a1 sin ωt and y = a2 sin( ωt + ϕ)
Then the general equation of Lissajou's figure can be obtained as 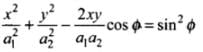

This is a straight line which passes through origin and its slope is a2/a1.
Lissajou's Figures in other conditions
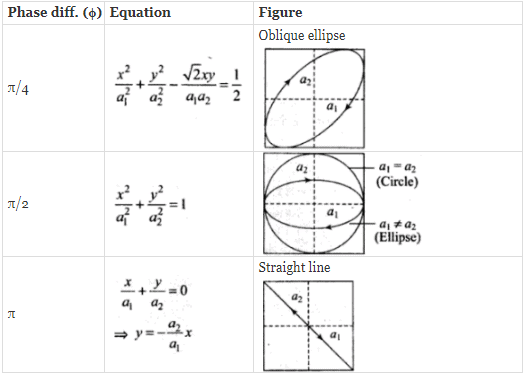
We have to find resultant - displacement by adding x and y-components. According to variation of x and y trajectory will be predicted.
Given, x = a cos ωt = a sin (ωt (π/2) ...(i)
And y = a sin ωt ...(ii)
Here a1 = a2 = a and ϕ = π/2
The trajectory of motion of the particle will be a circle of radius a.
Q.6. The displacement of a particle varies with time according to the relation
y = a sin ωt + b cos ωt
(a) The motion is oscillatory but not S.H.M.
(b) The motion is S.H.M. with amplitude a + b.
(c) The motion is S.H.M. with amplitude a2 + b2.
(d) The motion is S.H.M. with amplitude 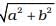 .
.
Ans. (d)
Solution.
y = a sin ωt + b cos ωt
The amplitude of motion is given by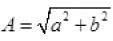
Hence, verifies the option (d).
Q.7. Four pendulums A, B, C and D are suspended from the same
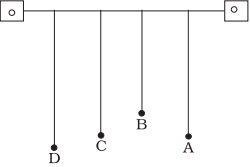
elastic support as A and C are of the same length, while B is smaller than A and D is larger than A. If A is given a transverse displacement,
(a) D will vibrate with maximum amplitude.
(b) C will vibrate with maximum amplitude.
(c) B will vibrate with maximum amplitude.
(d) All the four will oscillate with equal amplitude.
Ans. (b)
Solution.
Here A is given a transverse displacement. Through the elastic support the disturbance is transferred to all the pendulums.
A and C are having same length, hence they will be in resonance, because of their time period of oscillation. Since length of pendulums A and C is same and T =2 π√L/g , hence their time period is same and they will have frequency of vibration. Due to it, a resonance will take place and the pendulum C will vibrate with maximum amplitude.
Q.8. Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is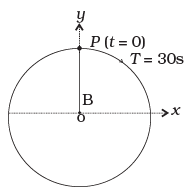
(a) 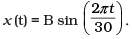
(b) 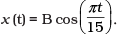
(c) 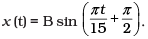
(d) 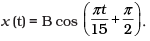
Ans. (a)
Solution.
Suppose a particle P is moving uniformly on a circle of radius A with angular speed. Q and R are the two feets of the perpendicular drawn from P on two diameters one along .Y-axis and the other along Y-axis.
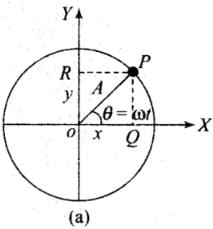
Suppose the particle P is on the X-axis at t = 0. Radius OP makes an angle with the X-axis at time t, then x = A cosωt and y = A sinωt
Here, x and v are the displacements of Q and R from the origin at time t, which are the displacement equations of SHM. It implies that although P is under uniform circular motion, Q and R are performing SHM about O with the same angular speed as that of P.
Let angular velocity of the particle executing circular motion is ω and when it is at P makes an angle θ as shown is the diagram.
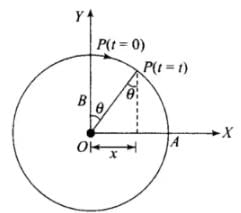
As 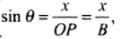
Clearly, ω = ωt
x = B sin θ = B (sin ωt) = B sin(πt/15)
x = B sin (2π/30 (t))
Q.9. The equation of motion of a particle is x = a cos (α t)2. The motion is
(a) Periodic but not oscillatory.
(b) Periodic and oscillatory.
(c) Oscillatory but not periodic.
(d) Neither periodic nor oscillatory.
Ans. (c)
Solution.
The equation of motion of a particle is
x = a cos(∝t)2
is a cosine function and x varies between -a and +a, the motion is oscillatory. Now checking for periodic motion, putting t+T in place of t. T is supposed as period of the function ω(t).
x(t + T) = a cos [α(t + T)]2
= a cos[α2t2 + α2t2 + 2α2tT] ≠ x(t)
Hence, it is not periodic.
Q.10. A particle executing S.H.M. has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s2. The period of oscillation is
(a) πs
(b) (π/2)s
(c) 2πs
(d) (π/t)s
Ans. Consider a SHM equation of motion
y = a sin ωt
v = dy/dt = aω cos ωt ...(i)
a = dv/dt = -aw sin ωt
a = -aω2 sin ωt ...(ii)
vmax = 30 cm/s (given)
vmax from (i)
vmax = aω
∴ aω = 30 ...(iii)
amax = aω2 from(ii)
60 = aω2 ...(iv) (given)
60 = ω x 30
ω = 2 rad/s
2π/T = 2
T = π. Verifies option (a).
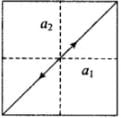
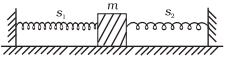
Q.11. When a mass m is connected individually to two springs S1 and S2, the oscillation frequencies are ν1 and ν2. If the same mass is attached to the two springs as shown in Figure, the oscillation frequency would be
(a) v1 + v2.
(b) 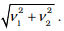
(c) 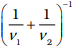
(d) 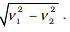
Ans. (b)
Solution.
When a mass (m) is connected to a spring on a horizontal frictionless surface then their frequencies are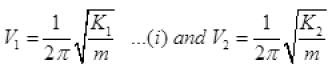
Now, the spring are in parallel because one end of both spring are connected with rigid body and other end to body. So their equivalent spring constant becomes kP = K1 + K2
And frequency 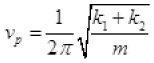
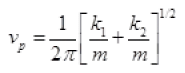
Form (i) 
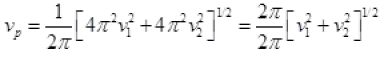

Hence, verifies the option (b).
MULTIPLE CHOICE QUESTIONS II
Q.12. The rotation of earth about its axis is
(a) Periodic motion.
(b) Simple harmonic motion.
(c) Periodic but not simple harmonic motion.
(d) Non-periodic motion.
Ans. (a, c)
Solution.
The motion of earth about its own axis is circular and complete its one complete revolution in regular interval of time. So it is periodic. But motion is not about a fixed point from which we can measure it’s displacement or about which it moves both side so it is not simple harmonic motion. So verifies the option (a) and (c).
Q.13. Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is
(a) Simple harmonic motion.
(b) Non-periodic motion.
(c) Periodic motion.
(d) Periodic but not S.H.M.
Ans. (a, c)
Solution.
For small angular displacement, the situation is shown in the figure. Only one restoring force creates motion in ball inside bowl.
Only one restoring force creates motion in ball inside bowl.
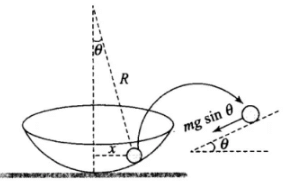
F = -mg sinθ
As θ is small, sin θ = θ
So, ma = -mg(x/R)
or, a = -(g/R)x ⇒ a ∝ -x
So, motion of the ball is S.H.M and periodic.
Q.14. Displacement vs. time curve for a particle executing S.H.M is shown in figure. Choose the correct statements.
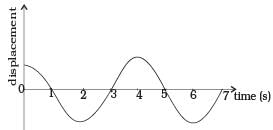
(a) Phase of the oscillator is same at t = 0 s and t = 2 s
(b) Phase of the oscillator is same at t = 2 s and t = 6 s.
(c) Phase of the oscillator is same at t = 1 s and t = 7 s.
(d) Phase of the oscillator is same at t = 1 s and t = 5 s.
Ans. (b, d)
Solution.
Two particles are said to be in same phase if the mode of vibration is same i.e., their distance will be nλ(/n = 1, 2, 3, ...)
(a) Distance between particles at t t = 0 and t = 2 is λ/2.
So, articles are not in same phase.
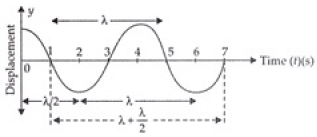
(b) As from figure the particles at t = 2 sec and 6 sec are at distance λ, so are in same phase.
(c) Particles at t =1, t= 7 are the distance 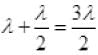 so are not in phase.
so are not in phase.
(d) Particles at t = 1 sec and 5 sec are at distance = λ so are in same phase.
Q.15. Which of the following statements is/are true for a simple harmonic oscillator?
(a) Force acting is directly proportional to displacement from the mean position and opposite to it.
(b) Motion is periodic.
(c) Acceleration of the oscillator is constant.
(d) The velocity is periodic.
Ans. (a, b, d)
Solution.
Consider a SHM x = a sin ωt. ...(i)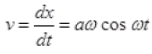 ...(ii)
...(ii)
Acceleration 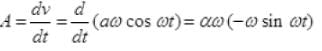
∴ A = -αω2 sin ωt or A = ω2x
mA = -mω2x
F ∝ -(x)
Hence, force is directly proportional to displacement opposite the direction of displacement. We can prove
x(t) = x(t+T)
So motion is periodic and SHM.
From (ii) v is also periodic as we can prove
v(t) = v(t + T)
Hence, verifies the option
Q.16. The displacement time graph of a particle executing S.H.M is shown in figure. Which of the following statement is/are true?
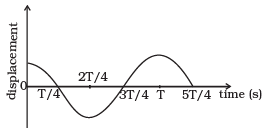
(a) The force is zero at t = 3T/4.
(b) The acceleration is maximum at y = 4T/4.
(c) The velocity is maximum at t = T/4.
(d) The P.E. is equal to K.E. of oscillation at t = T/2.
Ans. (a, b, c)
Solution.
(a) At t = 3T/4 Particle is at it’s mean position so force acting on it is zero, but it continue the motion due to inertia of mass, here a = 0, so F = 0.
(b) At t = 4T/4 = T, particle’s velocity changes increasing to decreases so maximum change in velocity at T. As acceleration = Change in velocity/Time, so acceleration is maximum here.
(c) At t = T/4 it is at its mean position where the velocity is maximum as no retarding force on it.
(d) t = T/2 = 2T/4, the particle has K.E = 0. So KE ≠ PE.
Hence, verifies the option (a,b,c)
Q.17. A body is performing S.H.M. Then its
(a) Average total energy per cycle is equal to its maximum kinetic energy.
(b) Average kinetic energy per cycle is equal to half of its maximum kinetic energy.
(c) Mean velocity over a complete cycle is equal to 2/π times of its maximum velocity.
(d) Root mean square velocity is 1/√2 times of its maximum velocity.
Ans. (a, b, d)
Solution.
In case of S.H.M, average total energy per cycle
= Maximum kinetic energy (K0)
= Maximum potential energy (U0)
Average K.E per cycle = 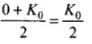
Let us write the equation for the SHM x = a sin ωt.
Clearly, it is a periodic motion as it involves sine function.
Let us find velocity of the particle, 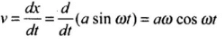
Mean velocity over a complete cycle,
So, 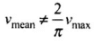
Root mean square speed,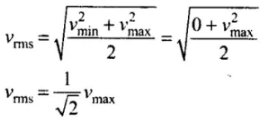
Q.18. A particle is in linear simple harmonic motion between two points A and B, 10 cm apart. Take the direction from A to B as the + ve direction and choose the correct statements.
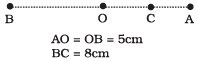
(a) The sign of velocity, acceleration and force on the particle when it is 3 cm away from A going towards B are positive.
(b) The sign of velocity of the particle at C going towards O is negative.
(c) The sign of velocity, acceleration and force on the particle when it is 4 cm away from B going towards A are negative.
(d) The sign of acceleration and force on the particle when it is at point B is negative.
Ans. (a, c, d)
Solution.

In option (a): When the particle is 3 cm away from A going towards B. So, velocity is towards AB, i.e. positive. In SHM, acceleration is always towards mean position (O) it means both force and acceleration act towards O, have positive sign.
Hence option (a) is correct.
In option (b): When the particle is at C, velocity is towards B hence positive. Hence option (b) is not correct.
In option (c): When the particle is 4 cm away from B going towards A velocity is negative and acceleration is towards mean position (O), hence negative. Hence option (c) is correct.
In option (d): Acceleration is always towards mean position (O). When the particle is at B, acceleration and force are towards BA that is negative. Hence option (d) is correct.
VERY SHORT ANSWER TYPE QUESTIONS
Q.1. Displacement versus time curve for a particle executing S.H.M. is shown in Figure, Identify the points marked at which (i) velocity of the oscillator is zero, (ii) speed of the oscillator is maximum.
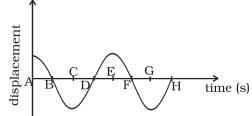
Ans. In displacement-time graph of SHM, zero displacement values correspond to mean position; where velocity of the oscillator is maximum. Whereas the crest and troughs represent amplitude positions, where displacement is maximum and velocity of the oscillator is zero.
(i) The points A, C, E, G lie at extreme positions (maximum displacement, y = A). Hence the velocity of the oscillator is zero.
(ii) The points B, D, F, H lie at mean position (zero displacement, y = 0). We know the speed is maximum at mean position.
Q.2. Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in Fig. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force
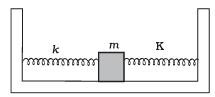
Ans. When mass is displaced from equilibrium position by a distance x towards right, the right spring gets compressed by x developing a restoring force kx towards left on the block. The left spring is stretched by an amount x developing a restoring force kx left on the block.
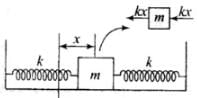
developing a restoring force kx towards left on the block.
F1 = -kx (for left spring) and
F2 = -kx (for right spring)
Restoring force, F = F1 + F2 = -2kx
∴ F = 2kx towards left.
Q.3. What are the two basic characteristics of a simple harmonic motion?
Ans. The two basic characteristics of a simple harmonic motion
(i) Acceleration is directly proportional to displacement.
(ii) The direction of acceleration is always towards the mean position, that is opposite to displacement.
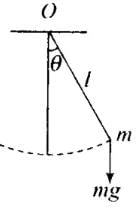
Q.4. When will the motion of a simple pendulum be simple harmonic?
Ans. Simple pendulum perform angular S.H.M. Consider the bob of simple pendulum is displaced through an angle θ shown. Q
The restoring torque about the fixed point O is
τ = mgl sinθ
If θ is small angle in radians, then sin θ = 0
⇒ mglθ
In vector form τ ∝ θ
Hence, motion of a simple pendulum is SHM for small angle of oscillations.
Q.5. What is the ratio of maxmimum acceleration to the maximum velocity of a simple harmonic oscillator?
Ans. Consider a SHM. x = A sin ωt
v = dx/dt = Aω cos ωt
For vmax cos ωt = -1
∴ vmax = Aω
a = dv/dt = -Aω2 sin ωt
For amax sing ωt = -1
amax = Aω2
∴ amax/vmax = Aω2/Aω = ω/1
Q.6. What is the ratio between the distance travelled by the oscillator in one time period and amplitude?
Ans. In the diagram shown a particle is executing SHM between P and Q. The particle starts from mean position ‘O’ moves to amplitude position ‘P’, then particle turn back and moves from ‘P’ to 'Q'. Finally the particle turns back again and return to mean position ‘O’. In this way the particle completes one oscillation in one time period.
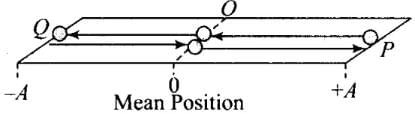
Total distance travelled while it goes from O → P → O → Q → O
= OP + PO + OQ + QO = A + A + A + A = 4A
Amplitude = OP = A
Hence, ratio of distance and amplitude = 4A/A = 4
Q.7. In Figure, what will be the sign of the velocity of the point P′ , which is the projection of the velocity of the reference particle P. P is moving in a circle of radius R in anticlockwise direction.
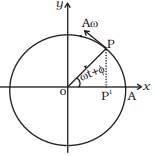
Ans. As the particle on reference circle moves in anti-clockwise direction. The projection will move from P’ to O towards left, i.e. from right to left, hence sign is negative.
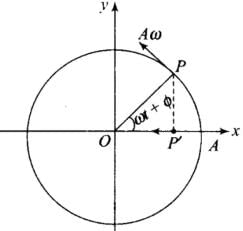
Q.8. Show that for a particle executing S.H.M, velocity and displacement have a phase difference of π/2.
Ans. Consider a SHM x = A sin ωt ...(i)
v = dx/dt = Aω cos ωt = Aω sin (90° + ωt)
(∵ sin (90° + θ) = cosθ)
∴ v = Aω sin (ωt + (π/2))
Phase of displacement from (i) is (ωt)
Phase of velocity from (ii) is (ωt + (π/2))
Hence, the phase difference = ωt +π/2 - ωt = π/2.
Q.9. Draw a graph to show the variation of P.E., K.E. and total energy of a simple harmonic oscillator with displacement.
Ans. The potential energy (PE) of a simple harmonic oscillator is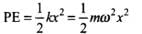 ...(i)
...(i)
When, PE is plotted against displacement x, we will obtain a parabola.
When x = 0, PE = 0.
When x = 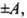 PE = maximum
PE = maximum
= 1/2 mω2A2
The kinetic energy (KE) of a simple harmonic oscillator KE = 1/2 mv2
But velocity of oscillator v = 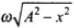
⇒ 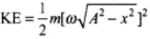
or KE = 1/2mω2(A2-x2) ...(ii)
This is also parabola, if we plot KE against displacement x.
i.e., KE = 0 at x = ±A
and KE = 1/2 mω2A2at x = 0
Now, total energy of the simple harmonic oscillator = PE + KE [using Eqs. (i) and (ii)]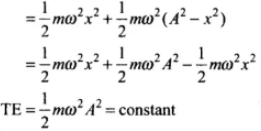
Which is a constant and independent of x.
Plotting under the above guidelines KE, PE and TE versus displacement x-graph as follows:
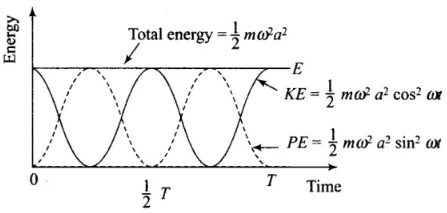
Important point: From the graph we note that potential energy or kinetic energy completes two vibrations in a time during which S.H.M. completes one vibration. Thus the frequency of potential energy or kinetic energy is double than that of S.H.M.
Q.10. The length of a second’s pendulum on the surface of Earth is 1m. What will be the length of a second’s pendulum on the moon?
Ans. A second's pendulum means a simple pendulum having time period T = 2s.
The time period of a simple pendulum T = 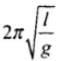
where, l = length of the pendulum and
g = acceleration due to gravity on surface of the earth.
Thus, 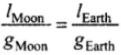
or 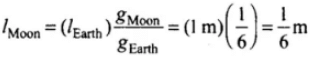
SHORT ANSWER TYPE QUESTIONS
Q.1. Find the time period of mass M when displaced from its equilibrium positon and then released for the system shown in Figure.
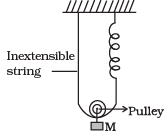
Ans. For observing oscillation, we have to displace the block slightly beyond equilibrium position and find the acceleration due to the restoring force.
Let in the equilibrium position, the spring has extended by an amount x0.
Tension in the spring = kx0
For equilibrium of the mass M, Mg = 2kx0
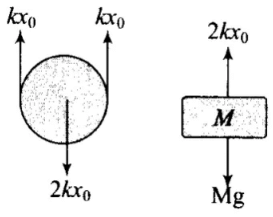
Let the mass be pulled through a distance y and then released. But, string is inextensible, hence the spring alone will contribute the total extension y + y = 2y, to lower the mass down by y from initial equilibrium mean position x0. So, net extension in the spring (x0 + 2y). From F.B.D of the block,
2k (x0 + 2y) - Mg = Ma
2kx0 + 4ky - Mg = Ma ⇒ Ma = 4ky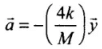
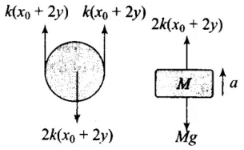
K and M being constant.
∴ a ∝ -x. Hence, motion is SHM
Comparing the above acceleration expression with standard SHM equation a = -ω2x, we get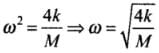
Q.2. Show that the motion of a particle represented by y = sin ω t - cos ω t is simple harmonic with a period of 2π/ω.
Ans. A function will represents S.H.M. if it can be written uniquely in the form of a or a sin (2π/T (t+ϕ))
Now y = sinωt - cosωt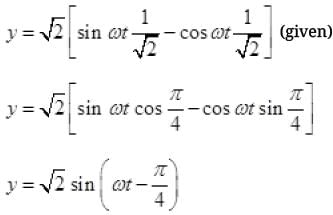
Comparing with standard SHM y = a s sin (2π/T(t+ϕ))
We get w = 2π/T or T = 2π/ω.
Q.3. Find the displacement of a simple harmonic oscillator at which its P.E. is half of the maximum energy of the oscillator.
Ans. Let us assume that the required displacement where PE is half of the maximum energy of the oscillator be x.
The potential energy of the oscillator at this position,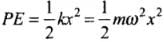 ...(i)
...(i)
Maximum energy of the oscillator = Maximum potential energy = Total energy
TE = 1/2 mω2A2 ...(ii)
where, A = amplitude of motion
We are given, PE = 1/2 TE
⇒ 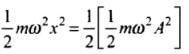
⇒ 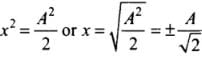
Q.4. A body of mass m is situated in a potential field U(x) = U0 (1-cos αx) when U0 and α are constants. Find the time period of small oscillations.
Ans. U = U0 (1 - cosα x)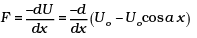
= -U0 α sin α x
= -U0 ααx (for small αx, sin αx - αx)
= -U0α2x
We know that F = -kx
So, k = U0α2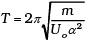
Q.5. A mass of 2 kg is attached to the spring of spring constant 50 Nm–1. The block is pulled to a distance of 5cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
Ans. x = 5 sin 5t
Q.6. Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
Ans. θ1 = θ0 sin(ωt + δ1)
θ2 = θ0 sin ((ωt + δ2)
For the first, θ = 2°, ∴ sin (ωt + δ1) = 1
For the 2nd, θ = -1°, ∴ sin (ωt + δ2) = -1/2
∴ ωt + δ1 = 90°, ωt + δ2 = -30°
∴ δ1 - δ2 = 120°
LONG ANSWER TYPE QUESTIONS
Q.1. A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s-1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
(a) Will there be any change in weight of the body, during the oscillation?
(b) If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
Ans. (a) Weight in weight machine will be due to the normal reaction (N) by platform. Consider the top position of platform, two forces due to weight of person and oscillator acts both downward.
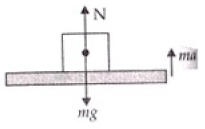
So motion is downward. Let with acceleration a then
ma = mg - N ...(i)
When platform lifts form its lowest position to upward
ma = N - mg ...(ii)
a = ω2A acceleration of oscillator
(i) ∴ Form (i) equation
N = mg - mω2A
Where A is amplitude, ω angular frequency, m mass of oscillator.
ω = 2πv = 2π x 2 = 4π rad/sec.
A = 5 cm = 5 x 10-2 m, m = 50 kg
N = 50 x 9.8 - 50 x 4π x 4π x 5 x 10-2
= 50[9.8 - 16π2 x 5 x 10-2]
= 50[9.8 - 80 x 3.14 x 3.14 x 10-2]
N = 50[9.8 - 7.89] = 50 x 1.91 = 95.50 N
So minimum weight is 95.50 N.
(ii) form (ii) N - mg = ma
For upward motion form lowest point of oscillator.
N = mg + ma = m(a+g)
= m[9.81 + ω2A] a = ω2A
= 50[9.81 + 16π2 x 5 x 10-2]
= 50[9.81 + 7.89] = 50 [ 17.70]
N = 885.00 N
(a) Hence, there is a change in weight of the body during oscillation.
(b) The maximum weight is 885 N, when platform moves from lowest to upward direction.
And the minimum is 95.5 N, when platform moves from highest point to downward direction.
Q.2. A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
(a) What is the amplitude of oscillation?
(b) Find the frequency of oscillation?
Ans. (a) when mass m is held in support by hand the extension in spring will be zero as no deforming force acts on spring.
Let the mass reaches at its new position unit displacement from previous.
Then P.E. of spring or mass = gravitational P.E. lost by man

P.E = mg x
But P.E. due to spring is 1/2 kx2k = ω2A
∴ 1/2 kx2 = mg x
x = 2mg/k
Mean position of spring by block will be when let extension is x0 then
F = +kx0
F= mg ∴ mg = +kx0 or x0 = mg/k ...(ii)
From (i) and (ii)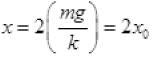
x = 4 cm ∴ 4 = 2x0
x0 = 2 cm.
The amplitude of oscillator is the maximum distance from mean position i.e., x - x0 = 4 - 2 = 2 cm.
(b) Time period T = 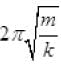 which does not depend on amplitude
which does not depend on amplitude
2mg/k = x from (i)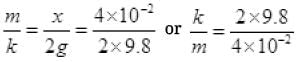
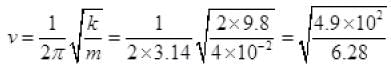
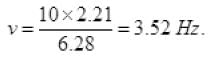
Oscillator will not rise above the positive from where it was released because total extension in spring is 4 cm when released and amplitude is 2 cm. So it oscillates below the released position.
Q.3. A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a time period.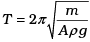
where m is mass of the body and ρ is density of the liquid.
Ans. When log is pressed downward into the liquid then and upward Buoyant force (B.F.) action it which moves the block upward and due to inertia it moves upward from its mean position due to inertia and then again come down due to gravity. So net restoring force on block = Buoyant force – mg
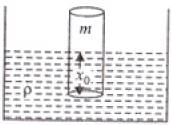
V = volume of liquid displaced by block
Let when floats then
mg = B.F. or mg = V ρg
mg = Ax0ρg ...(i)
A = area of cross-section
x0 = Height of block liquid
Let x height again dip in liquid when pressed into water total height of block in water = (x + x0)
So net restoring force = [A(x+x0)] ρ.g - mg
Frestoring = A x0ρg + Axρg - Ax0ρg
Frestoring = - Axpg
(as Buoyant force is upward and x is downward)
Frestoring = ∝ - x
So motion is SHM here k Aρg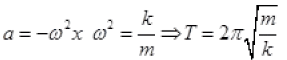
Frestoring = -Apgx
ma = - Apgx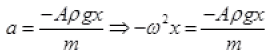
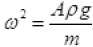
k = Aρg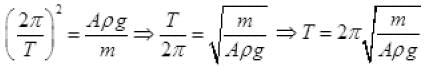
Q.4. One end of a V-tube containing mercury is connected to a suction pump and the other end to atmosphere. The two arms of the tube are inclined to horizontal at an angle of 45° each. A small pressure difference is created between two columns when the suction pump is removed. Will the column of mercury in V-tube execute simple harmonic motion? Neglect capillary and viscous forces. Find the time period of oscillation.
Ans. Consider the liquid in the length dx . It’s mass is A ρdx at a height x.
PE = A ρdx gx
The PE of the left column
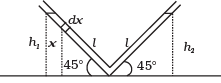
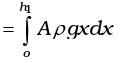
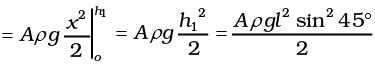
Similarly, P.E. of the right column 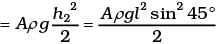
h1 = h2 = l sin 45° where l is the length of the liquid in one arm of the tube.
Total P.E. = Aρgh2 = Aρgl2 sin2 45°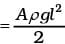
If the change in liquid level along the tube in left side in y, then length of the liquid in left side is l – y and in the right side is l + y.
Total P.E. = Aρg(l – y)2 sin2 45° + Aρg(l + y)2 sin2 45°
Change in PE = (PE)f – (PE)i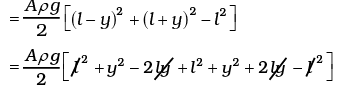
= Aρg [y2 + l2]
Change in K.E. = 1/2 Aρ2ly2
Change in total energy = 0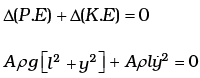
Differentiating both sides w.r.t. time,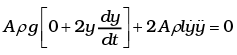
2Aρgy + 2 Aρly = 0
ly + gy = 0
y + g/l (y) = 0
ω2 = g/l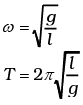
Q.5. A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
Ans. Acceleration due to gravity at P = g.x/R, where g is the acceleration at the surface.
Force = mgx/R = -k.x, k = mg/R
Motion will be SHM with time period 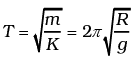
Q.6. A simple pendulum of time period 1 second and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Assume θ0 to be small so that sinθ0 θ0 and cosθ0 l.
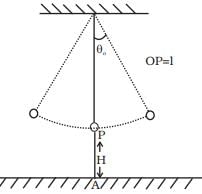
Ans. Assume that t = 0 when θ = θ0. Then,
θ = θ0 cos ωt
Given a seconds pendulum ω = 2π
At time t1, let θ = θ0/2
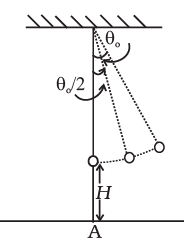
∴ 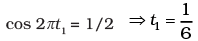
θ = -θ02π sin 2πt 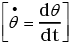
At t1 = 1/6
θ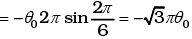
Thus the linear velocity is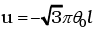 perpendicular to the string.
perpendicular to the string.
The vertical component is
uy = -√3πθ0lsinθ0
and the horizontal component is
ux = -√3πθ0lcosθ0
At the time it snaps, the vertical height is
H′ = H + l (1 – cos(θ0/2))
Let the time required for fall be t, then
H' = uyt + (1/2)gt2 (notice g is also in the negative direction)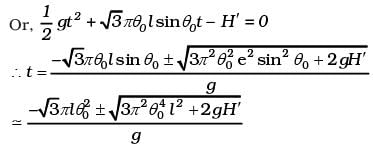
Neglecting terms of order θ20 and higher,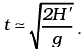
Now H' ≃ H + l (1 – 1) = H ∴ t ≈ 
The distance travelled in the x direction is uxt to the left of where it snapped.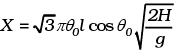
To order of θ0,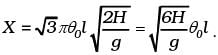
At the time of snapping, the bob was
l sinθ0≃lθ0 distance from A.
Thus, the distance from A is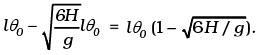
|
96 videos|367 docs|98 tests
|
FAQs on NCERT Exemplar: Oscillations - Physics Class 11 - NEET
| 1. What is an oscillation? |  |
| 2. What are the types of oscillations? |  |
| 3. What is the formula for the time period of an oscillating system? |  |
| 4. How does the amplitude affect oscillations? |  |
| 5. What is resonance in oscillations? |  |





















