NCERT Solutions Class 12 Chemistry Chapter 1 - Solutions
Page No.5 - Intext Questions
Q1.1. Calculate the mass percentage of benzene (C6H6) and carbon tetrachloride (CCl4) if 22 g of benzene is dissolved in 122 g of carbon tetrachloride.
Ans: 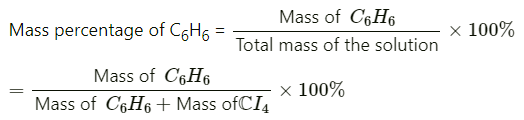
= 22/(22+122)x x 100%
= 15.28%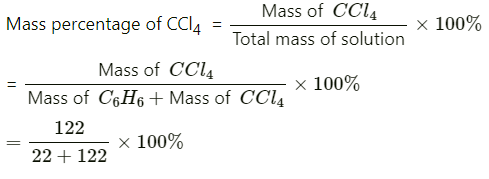
= 84.72%
Alternatively,
Mass percentage of CCl4 = (100 − 15.28)%
= 84.72%
Q1.2: Calculate the mole fraction of benzene in solution containing 30% by mass in carbon tetrachloride.
Ans:  Benzene
Benzene
Let the total mass of the solution be 100 g and the mass of benzene be 30 g.
∴ Mass of carbon tetrachloride = (100 − 30)g = 70 g
Molar mass of benzene (C6H6) = (6 × 12 + 6 × 1) g mol−1 = 78 g mol−1
∴ Number of moles of C6H6 = 30 /78 mol = 0.3846 mol
Molar mass of carbon tetrachloride (CCl4) = 1 × 12 + 4 × 355 = 154 g mol−1
∴ Number of moles of CCl4 = 70/154 mol = 0.4545 mol
Thus, the mole fraction of C6H6 is given as:
= 0.458
Q1.3: Calculate the molarity of each of the following solutions:
(a) 30 g of Co(NO3)2. 6H2O in 4.3 L of solution
(b) 30 mL of 0.5 M H2SO4 diluted to 500 mL.
Ans: Molarity is given by:
Molarity = Moles of solute/Volume of solution in litre
(a) Molar mass of Co (NO3)2.6H2O = 59 + 2 (14 + 3 × 16) + 6 × 18 = 291 g mol−1
∴ Moles of Co (NO3)2.6H2O = 30 / 291 mol = 0.103 mol
Therefore, molarity = 0.103 mol/4.3 L = 0.023 M
(b) Using M₁V₁ = M₂V₂
Where:
M₁ = initial molarity = 0.5 M
V₁ = initial volume = 30 mL = 0.03
V₂ = final volume = 500 mL = 0.5 L
Using M, 0.5 × 0.03 = M₂ × 0.5
Solve for M2
M2 = (0.5 × 0.03) / 0.5 = 0.015 / 0.5 = 0.03 M
Q1.4: Calculate the mass of urea (NH2CONH2) required in making 2.5 kg of 0.25 molal aqueous solution.
Ans: 0.25 Molal aqueous solution to urea means that
moles of urea = 0.25 mole
mass of solvent (NH2CONH2) = 60 g mol-1
∴ 0.25 mole of urea = 0.25 x 60=15g
Mass of solution = 1000+15 = 1015g = 1.015 kg
1.015 kg of urea solution contains 15g of urea
∴ 2.5 kg of solution contains urea =15/1.015 x 2.5 = 37 g
Q1.5: Calculate (a) molality (b) molarity and (c) mole fraction of KI if the density of 20% (mass/mass) aqueous KI is 1.202 g mL-1.
Ans:
(a) Molar mass of KI = 39 + 127 = 166 g mol−1
20% (mass/mass) aqueous solution of KI means 20 g of KI is present in 100 g of solution.
That is,
20 g of KI is present in (100 − 20) g of water = 80 g of water
Therefore,
Molality of the solution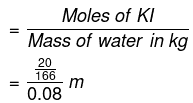
= 1.506 m
= 1.51 m (approximately)
(b) It is given that the density of the solution = 1.202 g mL−1
∴ Volume of 100 g solution = Mass / Density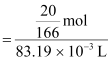
= 83.19 mL
= 83.19 × 10−3 L
Therefore, molarity of the solution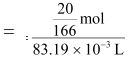
= 1.45 M
(c) Moles of Kl = 20/166 = 0.12 mol
Moles of water = 80/18 = 4.44
Therefore, mole fraction of Kl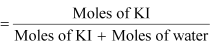
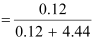
= 0.0263
Page No.9 - Intext Questions
Q1.6: H2S, a toxic gas with rotten egg like smell, is used for the qualitative analysis. If the solubility of H2S in water at STP is 0.195 m, calculate Henry’s law constant.
Ans:  H2SIt is given that the solubility of H2S in water at STP is 0.195 m, i.e., 0.195 mol of H2S is dissolved in 1000 g of water.
H2SIt is given that the solubility of H2S in water at STP is 0.195 m, i.e., 0.195 mol of H2S is dissolved in 1000 g of water.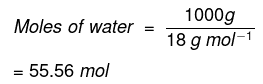
∴ Mole fraction of H2S,

At STP, pressure (p) = 0.987 bar
According to Henry’s law:
p = KHx
= 0.987 / 0.0035 Bar
= 282 bar
Solubility of H₂S in water at STP = 0.195 m (molality)
Pressure at STP = 0.987 bar
We need to find Henry's law constant (K).
Step 1: Calculate the mole fraction (x) of H2S:
- Molality = 0.195 mol/kg
- Moles of water in 1 kg = 1000 g / 18 g/mol = 55.56 mol
- Mole fraction of H₂S:
x = 0.195 / (0.195 + 55.56) ≈ 0.0035
Step 2: Apply Henry's Law:
- According to Henry’s Law: p = K × x
- K = p / x = 0.987 bar / 0.0035 ≈ 282 bar
Henry’s law constant (K) = 282 bar.
Q1.7: Henry’s law constant for CO2 in water is 1.67 × 108 Pa at 298 K. Calculate the quantity of CO2 in 500 mL of soda water when packed under 2.5 atm CO2 pressure at 298 K.
Ans: It is given that: KH = 1.67 × 108 Pa
pco2 = 2.5 atm = 2.5 × 1.01325 × 105 Pa
= 2.533125 × 105 Pa
According to Henry’s law:
= 0.00152
We can write,
[Since, is negligible as compared to ]
In 500 mL of soda water, the volume of water = 500 mL
[Neglecting the amount of soda present]
We can write:
500 mL of water = 500 g of water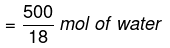
= 27.78 mol of water
Now,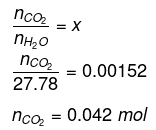
Hence, quantity of CO2 in 500 mL of soda water = (0.042 × 44)g
= 1.848 g
Page No.15 - Intext Questions
Q1.8: The vapour pressure of pure liquids A and B are 450 and 700 mm Hg respectively, at 350 K. Find out the composition of the liquid mixture if total vapour pressure is 600 mm Hg. Also find the composition of the vapour phase.
Ans: It is given that: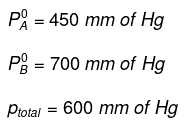
from Rault's law, we have: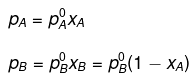
Therefore, total pressure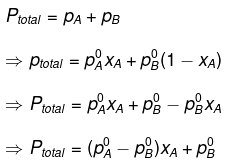
⇒ 600 = (450 - 700) xA + 700
⇒ - 100 = -250xA
⇒ xA = 0.4
Therefore, xB = 1 - xA
= 1 - 0.4
= 0.6
Now,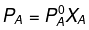
= 450 × 0.4
= 180 mm of Hg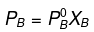
= 700 × 0.6
= 420 mm of Hg
Now, in the vapour phase:
Mole fraction of liquid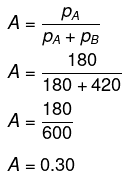
And, mole fraction of liquid B = 1 − 0.30 = 0.70
Page No.23 - Intext Questions
Q1.9: Vapour pressure of pure water at 298 K is 23.8 mm Hg. 50 g of urea (NH2CONH2) is dissolved in 850 g of water. Calculate the vapour pressure of water for this solution and its relative lowering.
Ans: It is given that vapour pressure of water, p01 = 23.8 mm of Hg
Weight of water taken, w1 = 850 g
Weight of urea taken, w2 = 50 g
Molecular weight of water, M1 = 18 g mol−1
Molecular weight of urea, M2 = 60 g mol−1
Now, we have to calculate vapour pressure of water in the solution. We take vapour
pressure as p1.
Now, from Raoult’s law, we have:
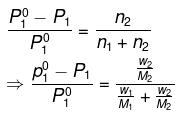

Hence, the vapour pressure of water in the given solution is 23.4 mm of Hg and its relative lowering is 0.0173.
Q1.10: Boiling point of water at 750 mm Hg is 99.63°C. How much sucrose is to be added to 500 g of water such that it boils at 100°C. Molal elevation constant for water is 0.52 K kg mol−1.
Ans: Here, elevation of boiling point
ΔTb = (100 273) − (99.63 273)
= 0.37 K
Mass of water, wl = 500 g
Molar mass of sucrose (C12H22O11), M2 = 12 × 12 + 22 × 1 + 11 × 16
= 342 g mol−1
Molal elevation constant, Kb = 0.52 K kg mol−1
We know that:
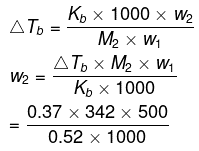
= 121.67 g (approximately)
Hence, 121.67 g of sucrose is to be added.
Note: There is a slight variation in this answer and the one given in the NCERT textbook.
Q1.11: Calculate the mass of ascorbic acid (Vitamin C, C6H8O6) to be dissolved in 75 g of acetic acid to lower its melting point by 1.5°C. Kf = 3.9 K kg mol−1.
Ans: Mass of acetic acid, w1 = 75 g
Molar mass of ascorbic acid (C6H8O6), M2 = 6 × 12 + 8 × 1 + 6 × 16
= 176 g mol−1
Lowering of melting point, ΔTf = 1.5 K
We know that: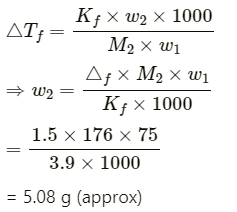
Hence, 5.08 g of ascorbic acid is needed to be dissolved.
Q1.12: Calculate the osmotic pressure in pascals exerted by a solution prepared by dissolving 1.0 g of polymer of molar mass 185,000 in 450 mL of water at 37°C.
Ans: It is given that:
Volume of water, V = 450 mL = 0.45 L
Temperature, T = (37 + 273)K = 310 K
Number of moles of the polymer, n = 1/18500 mol
We know that: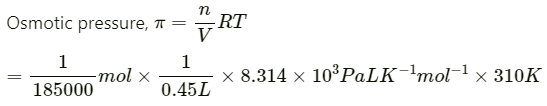
= 30.98 Pa
= 31 Pa(approximately)
Exercises
Q1.1: Define the term solution. How many types of solutions are formed? Write briefly about each type with an example.
Ans: Homogeneous mixtures of two or more than two components are known as solutions.
There are three types of solutions.
(i) Gaseous solution: The solution in which the solvent is a gas is called a gaseous solution. In these solutions, the solute may be liquid, solid, or gas.
Example: a mixture of oxygen and nitrogen gas is a gaseous solution.
(ii) Liquid solution: The solution in which the solvent is a liquid is known as a liquid solution. The solute in these solutions may be gas, liquid, or solid.
Example: a solution of ethanol in water is a liquid solution.
(iii) Solid solution: The solution in which the solvent is a solid is known as a solid solution. The solute may be gas, liquid or solid. For example, a solution of copper in gold is a solid solution.
Q1.2: Give an example of solid solution in which the solute is a gas.
Ans: In case a solid solution is formed between two substances (one having very large particles and the other having very small particles), an interstitial solid solution will be formed.
Example: a solution of hydrogen in palladium is a solid solution in which the solute is a gas.
|
75 videos|278 docs|78 tests
|
FAQs on NCERT Solutions Class 12 Chemistry Chapter 1 - Solutions
| 1. What are the different types of solutions? |  |
| 2. How can you determine the concentration of a solution? |  |
| 3. What is the difference between a saturated solution and an unsaturated solution? |  |
| 4. How does temperature affect the solubility of a solute in a solvent? |  |
| 5. What is the difference between a homogeneous and a heterogeneous solution? |  |

















