NEET Previous Year Questions (2014-2025): Dual Nature of Radiation & Matter | Physics Class 12 PDF Download
2025
Q1: De-Broglie wavelength of an electron orbiting in the n = 2 state of hydrogen atom is close to: (Given: Bohr radius = 0.052 nm) [NEET 2025]
(a) 1.67 nm
(b) 2.67 nm
(c) 0.067 nm
(d) 0.67 nm
Ans: (d)
Given n = 2, Z = 1
2πr = nλ
2π × (0.052 × n2 / Z) = nλ
On solving, λ = 0.67 nm
Q2: Which of the following options represents the variation of photoelectric current with the property of light shown on the x-axis?
(A)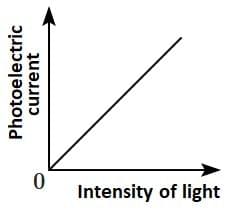 (B)
(B) 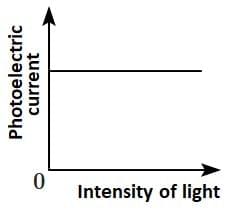 (C)
(C) 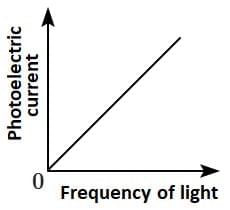 (D)
(D) 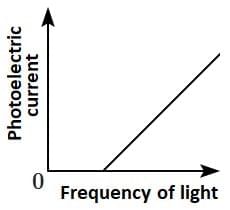 [NEET 2025]
[NEET 2025]
Option
(a) (A) and (D)
(b) (B) and (D)
(c) A Only
(d) A and (c)
Ans: (c) 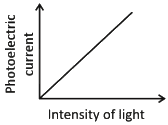
Photoelectric current is directly proportional to the intensity of light.
According to Einstein’s photoelectric equation, when light of sufficient frequency falls on a metal surface, it causes the emission of photoelectrons. The kinetic energy of the emitted electrons depends on the frequency of light, while the number of emitted electrons (and hence the photoelectric current) is directly proportional to the intensity of incident light.
This is because higher intensity means more photons striking the surface per second, leading to more electrons being emitted, which increases the current linearly as shown in the graph.
Q3: A photon and an electron (mass m) have the same energy E. The ratio (λphoton/λelectron) of their de Broglie wavelengths is: (c is the speed of light) [NEET 2025]
(a) 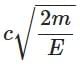
(b) 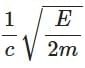
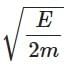
(d) 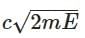
Ans: (a)
The de-Brogile wavelength is given by: λ = h / √(2mE)
For electron: λe = h / √(2mE)
For photon: E = pc ⇒ λPh = hc / E
⇒ λe / λPh = (h / √(2mE)) × (E / hc) = √(E / 2m) × (1 / c)
⇒ λPh / λe = 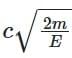
2024
Q1: If c is the velocity of light in free space, the correct statements about photon among the following are:A. The energy of a photon is E = hv.
B. The velocity of a photon is c.
C. The momentum of a photon, p = hv / c.
D. In a photon-electron collision, both total energy and total momentum are conserved.
E. Photon possesses positive charge.
Choose the correct answer from the options given below:
(a) A and B only
(b) A, B, C and D only
(c) A, C and D only
(d) A, B, D and E only [NEET 2024]
Ans: (b)
A. The energy of a photon is E = hv.
This statement is correct. The energy of a photon is given by the equation:
E = hv
where
E is the energy, h is Planck's constant, and v (also written as ν) is the frequency of the photon.
B. The velocity of a photon is c.
This statement is also correct. In free space (vacuum), the velocity of light, and hence the velocity of a photon, is constant and is denoted by c.
C. The momentum of a photon, p = hv / c.
This statement is correct as well. The momentum p of a photon can be expressed as:
p = E / c = hv / c
D. In a photon-electron collision, both total energy and total momentum are conserved.
This statement is correct. During collisions involving photons and electrons, such as Compton scattering, both energy and momentum are conserved.
E. Photon possesses positive charge.
This statement is incorrect. Photons are electrically neutral particles and do not possess any charge.
Based on the analysis, the correct statements are A, B, C, and D. Therefore, the correct answer is:
Option B
A, B, C, and D only
Q2: The graph which shows the variation of (1 / λ2) and its kinetic energy, E is (where λ is de Broglie wavelength of a free particle):
(a) 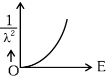
(b) 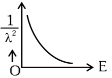
(c) 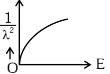
(d) 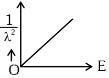 [NEET 2024]
[NEET 2024]
Ans: (d)
de-Broglie wavelength 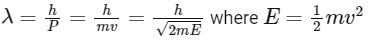
Squaring both sides,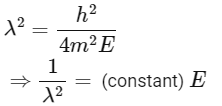
Graph passes through origin with constant slope.
Q3: Radiation of wavelength 280 nm is used in an experiment of photoelectric effect with cathode of work function 2.5 eV. The maximum kinetic energy of the photoelectrons is: [NEET 2024]
(Take h = 6.62 × 10⁻³⁴ J·s and c = 3 × 10⁸ m/s)
(a) 4.4 eV
(b) 7.103 × 10⁻¹⁵ J
(c) 1.9 eV
(d) 4.60 eV
Ans: (c)
To solve this problem, we will use the photoelectric effect equation:
K.E. (max) = Eₛ - W
Where:
K.E. (max) is the maximum kinetic energy of the emitted photoelectron.
Eₛ is the energy of the incident photon, which is given by the equation Eₛ = h * f, where f is the frequency of the radiation.
W is the work function of the material (given as 2.5 eV in this case).
Step 1: Convert the wavelength to frequency
The wavelength (λ) is given as 280 nm (which is 280 × 10⁻⁹ m). The frequency f can be calculated using the relationship:
f = c / λ
Where:
c is the speed of light (3 × 10⁸ m/s),
λ is the wavelength.
Now, calculate the frequency:
f = (3 × 10⁸ m/s) / (280 × 10⁻⁹ m) = 1.071 × 10¹⁵ Hz
Step 2: Calculate the energy of the incident photon
The energy of the photon is given by:
Eₛ = h * f
Where:
h is Planck's constant (6.62 × 10⁻³⁴ J·s),
f is the frequency calculated earlier.
Now, calculate the energy:
Eₛ = (6.62 × 10⁻³⁴ J·s) * (1.071 × 10¹⁵ Hz) = 7.09 × 10⁻¹⁹ J
Step 3: Convert the energy to eV
To convert the energy from joules to electron volts (eV), we use the conversion factor 1 eV = 1.6 × 10⁻¹⁹ J:
Eₛ = (7.09 × 10⁻¹⁹ J) / (1.6 × 10⁻¹⁹ J/eV) = 4.44 eV
Step 4: Calculate the maximum kinetic energy of the photoelectron
The maximum kinetic energy is:
K.E. (max) = Eₛ - W
Where W = 2.5 eV (work function of the cathode).
Now, calculate the kinetic energy:
K.E. (max) = 4.44 eV - 2.5 eV = 1.94 eV
Conclusion: The maximum kinetic energy of the photoelectron is approximately 1.9 eV.
Q4: Given below are two statements: [NEET 2024]
Statement I: The de Broglie wavelength associated with a material particle depends on its charge and nature.
Statement II: The wave nature of particles in the sub-atomic domain is significant and measurable.
In the light of the above statements, choose the most appropriate answer from the options given below:
(a) Both Statement I and Statement II are correct.
(b) Both Statement I and Statement II are incorrect.
(c) Statement I is correct but Statement II is incorrect.
(d) Statement I is incorrect but Statement II is correct.
Ans: (d)
Statement I: The de Broglie wavelength associated with a material particle depends on its charge and nature.
The de Broglie wavelength of a particle is given by the formula:
λ = h / mv
Where:
- λ is the de Broglie wavelength,
- h is Planck's constant,
- m is the mass of the particle,
- v is the velocity of the particle.
Charge and nature of the particle do not directly affect the de Broglie wavelength according to this formula. The de Broglie wavelength is primarily dependent on the mass and velocity of the particle. The charge of the particle does not influence the de Broglie wavelength directly.
Therefore, Statement I is incorrect.
Statement II: The wave nature of particles in the sub-atomic domain is significant and measurable.
In the sub-atomic domain, particles like electrons do exhibit wave-particle duality. This means they exhibit both particle-like and wave-like properties. The wave nature of sub-atomic particles is significant and measurable in certain cases, such as in the electron microscope or diffraction experiments.
Statement II is correct, as the wave nature of particles like electrons can be observed in experiments such as electron diffraction.
Conclusion: Statement I is incorrect, and Statement II is correct.
Correct Answer: (d) Statement I is incorrect but Statement II is correct.
Q5: An electron and an alpha particle are accelerated by the same potential difference. Let λe and λα denote the de-Broglie wavelengths of the electron and the alpha particle, respectively. Then: [NEET 2024]
(a) λe > λα
(b) λe = 4λα
(c) λe = λα
(d) λe< λα
Ans: (a)
de-Broglie wavelength is given by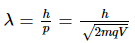
For same potential difference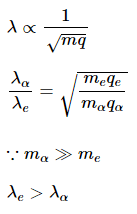
Correct answer is (a) λe > λα
Q6: If Φ is the work function of photosensitive material in electron-volts and light of a wavelength of numerical value λ = hc/e meters is incident on it with energy above its threshold value at an instant, then the maximum kinetic energy of the photo-electron ejected by it at that instant is (in SI units): [NEET 2024]
(a) e + 2Φ
(b) 2e − Φ
(c) e − Φ
(d) e + Φ
Ans: (c)
Given Data:
- Φ is the work function of the photosensitive material in electron-volts (eV).
- The wavelength λ is given by λ = hc / emeters, where:
- h is Planck's constant,
- c is the speed of light,
- e is the elementary charge (in Coulombs).
Step 1: Energy of the Photon
The energy of the incoming photon can be calculated as:
Ephoton = hc / λ
Substitute the given wavelength λ = hc / e:
Ephoton = hc / (hc / e) = e eV
So, the energy of the photon is e eV.
Step 2: Maximum Kinetic Energy of the Photoelectron
The maximum kinetic energy of the photoelectron is given by:
K.E. = Ephoton - Φ
Substitute the values:
K.E. = e - Φ
Conclusion: The maximum kinetic energy of the photoelectron in SI units is e - Φ.
Correct Answer: (c) e - Φ.
2023
Q1: The work functions of Caesium (Cs), Potassium (K), and Sodium (Na) are 2.14 eV, 2.30 eV, and 2.75 eV respectively. If incident electromagnetic radiation has an incident energy of 2.20 eV, which of these photosensitive surfaces may emit photoelectrons? (NEET 2023)
A: Cs only
B: Both Na and K
C: K only
D: Na only
Ans: A
Solution: Energy of incident radiation = 2.80 eV
The work function of Cs → 2.14 eV
The work function of K → 2.30 eV
The work function of Na → 2.75 eV
Since the work functions of potassium and sodium are more than the energy of incident radiation hence photons may be emitted from cesium.
Q2: The minimum wavelength of X-rays produced by an electron accelerated through a potential difference of V volts is proportional to : (NEET 2023)
(a) 1/V
(b) 1/√V
(c) V2
(d) √V
Ans: (a)
Minimum wavelength of X-Rays is
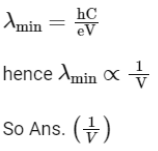
Q3: The de-Broglie wavelength associated with an electron, accelerated by a potential difference of 81 V is given by: (NEET 2023)
(a) 13.6 nm
(b) 136 nm
(c) 1.36 nm
(d) 0.136 nm
Ans: (d)
To calculate the de-Broglie wavelength associated with an electron accelerated by a potential difference, we can use the following formula for de-Broglie wavelength:
λ = h / p
where:
- λ is the de-Broglie wavelength,
- h is Planck's constant (6.626 × 10⁻³⁴ J·s),
- p is the momentum of the electron.
The momentum p can be related to the kinetic energy gained by the electron due to acceleration by the potential difference V:
K.E. = eV
where e is the charge of the electron (1.6 × 10⁻¹⁹ C) and V is the potential difference (81 V).
Since K.E. = (1/2)mv² = p² / (2m), we can find the momentum p as:
p = √(2m eV)
where:
- m is the mass of the electron (9.11 × 10⁻³¹ kg),
- e is the electron charge (1.6 × 10⁻¹⁹ C),
- V is the potential difference (81 V).
Step 1: Calculate the Momentum p
Using the given values:
p = √(2 × 9.11 × 10⁻³¹ kg × 1.6 × 10⁻¹⁹ C × 81 V)
Now, calculate the momentum:
p ≈ √(2.35 × 10⁻²⁸ kg·C·V)
p ≈ 1.53 × 10⁻²⁹ kg·m/s
Step 2: Calculate the de-Broglie Wavelength λ
Now, using the de-Broglie formula:
λ = h / p
Substitute the values:
λ = 6.626 × 10⁻³⁴ J·s / 1.53 × 10⁻²⁹ kg·m/s
λ ≈ 4.33 × 10⁻⁶ m
λ ≈ 0.136 nm
Correct Answer: (d) 0.136 nm.
Q4: The maximum kinetic energy of the emitted photoelectrons in the photoelectric effect is independent of the: (NEET 2023)
(a) work function of material
(b) intensity of incident radiation
(c) frequency of incident radiation
(d) wavelength of incident radiation
Ans: (b)
The maximum kinetic energy of the emitted photoelectrons in the photoelectric effect is governed by the photoelectric equation:
K.E. = Ephoton - Φ
Where:
- K.E. is the maximum kinetic energy of the emitted photoelectron,
- E(photon) is the energy of the incident photon,
- Φ is the work function of the material (the minimum energy required to eject an electron from the surface).
The energy of the incident photon is related to the frequency f of the radiation by:
Ephoton = h * f
Where:
- h is Planck's constant,
- f is the frequency of the incident radiation.
From this, we can conclude:
The maximum kinetic energy of the photoelectrons depends on the frequency of the incident radiation (since energy is proportional to frequency) and the work function of the material.
Analysis of the Options:
(a) Work function of material: The work function affects the energy required to eject an electron, and hence it does affect the maximum kinetic energy.
(b) Intensity of incident radiation: The intensity of the incident radiation affects the number of photoelectrons emitted but does not affect the maximum kinetic energy. The kinetic energy depends only on the frequency of the radiation.
(c) Frequency of incident radiation: The maximum kinetic energy of the emitted electrons depends on the frequency of the incident radiation (higher frequency leads to higher energy photons, thus higher kinetic energy).
(d) Wavelength of incident radiation: The wavelength is related to the frequency by f = c / λ (where c is the speed of light), so the maximum kinetic energy of the emitted electrons is dependent on the wavelength via the frequency.
Conclusion: The maximum kinetic energy of the photoelectrons is independent of the intensity of the incident radiation.
Correct Answer: (b) intensity of incident radiation.
2022
Q1: The light rays having photons of energy 4.2 eV are falling on a metal surface having a work function of 2.2 eV. The stopping potential of the surface is
(a) 6.4 V
(b) 2 eV
(c) 2 V
(d) 1.1 V
Ans: (c)
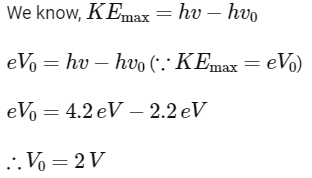
Q2: The threshold frequency of a photoelectric metal is v0. If light of frequency 4v0 is incident on this metal, then the maximum kinetic energy of emitted electrons will be :
(a) 4 hv0
(b) hv0
(c) 2 hv0
(d) 3 hv0
Ans: (d)
According to Einstein's photoelectric equation
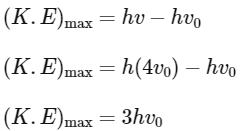
Q3: When two monochromatic lights of frequency, ν and ν/2 are incident on a photoelectric metal, their stopping potential becomes Vs/2 and Vs respectively. The threshold frequency for this metal is
A: 3ν
B: 2/3ν
C: 3/2ν
D: 2ν
Ans: (c)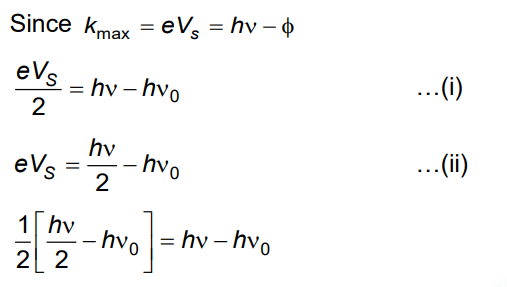
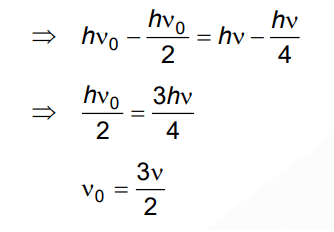
2021
Q1: The number of photons per second on average emitted by the source of monochromatic light of wavelength 600 nm, when it delivers the power of 3.3 × 10–3 watts will be : (h = 6.6 × 10–34 Js)
A: 1016
B: 1015
C: 1018
D: 1017
Ans: A
Solution: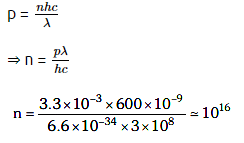
Q2: An electromagnetic wave of wavelength 'λ' is incident on a photosensitive surface of negligible work function. If 'm' is the mass of photoelectron emitted from the surface that has de-Broglie wavelength λd, then:
A: 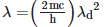
B: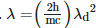
C: 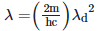
D: 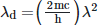
Ans: A
Solution: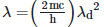
2020
Q1: Light of frequency 1.5 times the threshold frequency is incident on a photosensitive material. What will be the photoelectric current if the frequency is halved and the intensity is doubled?
A: one-fourth
B: Zero
C: doubled
D: four times
Ans: B
Solution:
f0 < f1 = 1.5 f0
∴ f2 = 0.75 f0
for given condition
fincident < fthreshold
so no photo electron emission
i = 0
Q2: The de-Broglie wavelength of an electron moving with kinetic energy of 144 eV is nearly
(a) 102 × 10−3 nm
(b) 102 × 10−4 nm
(c) 102 × 10−5 nm
(d) 102 × 10−2 nm
Ans: (d)
Kinetic energy of electron, K = 144 eV
⇒ eV = 144 eV
⇒ V = 144 V
∴ de-Broglie wavelength
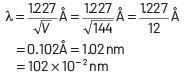
Q3: The wave nature of electrons was experimentally verified by
(a) de-Broglie
(b) Hertz
(c) Einstein
(d) Davisson and Germer
Ans: (d)
The wave nature of electrons was experimentally verified by Davisson and Germer.
2019
Q1: An electron is accelerated through a potential difference of 10,000 V. Its de-Broglie wavelength is, (nearly) : (me = 9 × 10–31 kg)
A: 12.2 × 10–13 m
B: 12.2 × 10–12 m
C: 12.2 × 10–14 m
D: 12.2 nm
Ans: B
For an electron accelerated through a potential V
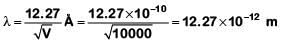
Q2: The work function of a photosensitive material is 4.0 eV.
This longest wavelength of light that can cause photon emission from the substance is (approximately)
(a) 3100 nm
(b) 966 nm
(c) 31 nm
(d) 310 nm
Ans: (d)
The work function of material is given by
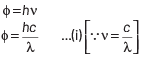
where, h = Planck’s constant = 6.63 × 10−34 J-s
c = speed of length = 3 × 108 ms−1
and λ = wavelength of light
Here, φ = 4 eV = 4 × 1.6 × 10 −19 J
Substituting the given values in Eq. (i), we get
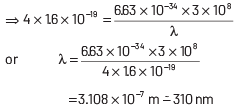
Q3: An electron is accelerated through a potential difference of 10,000 V.
Its de-Broglie wavelength is, (nearly) : (m e = 9 × 10−31 kg)
(a) 12.2 × 10−12 m
(b) 12.2 × 10−14m
(c) 12.2 nm
(d) 12.2 × 10−13m
Ans: (a)
Given, potential difference, V = 10000 V If electron is accelerated through a potential of V volt, then the wavelength associated with it is given by
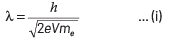
where, h = Planck’s constant = 6.63 × 10−34 J-s,
e = electronic charge = 1.6 × 10−19 C a
nd me = mass of electron = 9 × 10−31 kg Substituting these values in Eq. (i),
we get
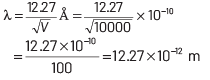
2018
Q1: An electron of mass m with an initial velocity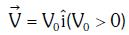 enters an electric field
enters an electric field 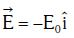 E0 = constant > 0) at t = 0. If λ0 is its de-Broglie wavelength initially, then its de-Broglie wavelength at time t is:
E0 = constant > 0) at t = 0. If λ0 is its de-Broglie wavelength initially, then its de-Broglie wavelength at time t is:
A: 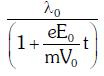
B: 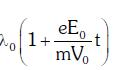
C: λ0t
D: λ0
Ans: A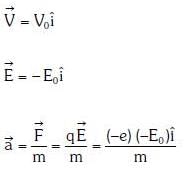
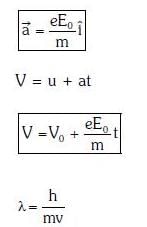
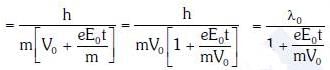
Q2: When the light of frequency 2v0 (where v0 is threshold frequency), is incident on a metal plate, the maximum velocity of electrons emitted is v1. When the frequency of the incident radiation is increased to 5 v0, the maximum velocity of electrons emitted from the same plate is v2. The ratio of v1 to v2 is :-
A: 1 : 2
B: 1 : 4
C: 4 : 1
D: 2 : 1
Ans: A
Solution:
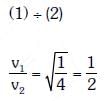
Q3: When the light of frequency 2ν0 (where, ν0 is threshold frequency), is incident on a metal plate, the maximum velocity of electrons emitted is v1 . When the frequency of the incident radiation is increased to 5ν0 , the maximum velocity of electrons emitted from the same plate is v2 . The ratio of v1 to v2 is
(a) 4 : 1
(b) 1 : 4
(c) 1 : 2
(d) 2 : 1
Ans: (c)
According to the Einstein’s photoelectric equation,
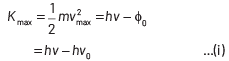
where, Kmax is the maximum kinetic energy of photoelectrons having maximum velocity vmax. When incident frequency of light, v = 2v0 Substituting the value of ν in Eq. (i), we get
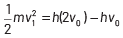
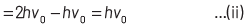
If incident frequency of radiation, ν = 5ν0 Substituting the value of ν in Eq. (i), we get
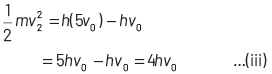
On dividing Eq. (ii) by Eq (iii), we get
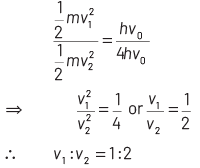
2017
Q1: The photoelectric threshold wavelength of silver is 3250 × 10–10m. The velocity of the electron ejected from a silver surface by ultraviolet light of wavelength 2536 × 10–10 m is:
(Given h = 4.14 × 10–15 eVs and c = 3 × 108 ms–1)
A: ≈ 0.6 × 106 ms–1
B: ≈ 61 × 103 ms–1
C: ≈ 0.3 × 106 ms–1
D: ≈ 6 × 105 ms–1
Ans: A
Solution:
Q2: The de-Broglie wavelength of a neutron in thermal equilibrium with heavy water at a temperature T (Kelvin) and mass m, is
(a) 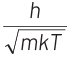
(b) 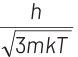
(c) 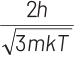
(d) 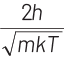
Ans: (b)
Thinking Process de-Broglie wavelength associated with a moving particle can be given as
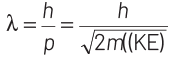
At thermal equilibrium, temperature of neutron and heavy water will be same. This common temperature is given as, T. Also, we know that, kinetic energy of a particle
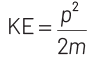
where, p = momentum of the particle m = mass of the particle Kinetic energy of the neutron is
K.E. = 3/2 kT
∴ de-Broglie wavelength of the neutron
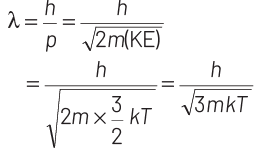
2016
Q1: When a metallic surface is illuminated with radiation of wavelength λ the stopping potential is V. If the same surface is illuminated with radiation of wavelength 2λ, the stopping potential is V/4. The threshold wavelength for the metallic surface is :
A: 3λ
B: 4λ
C: 5λ
D: 5/2λ
Ans: A
When a metallic surface is illuminated with radiation of wavelength λ, the stopping potential is V.
The photoelectric equation can be written as,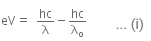
Now, when the same surface is illuminated with radiation of wavelength 2λ, the stopping potential is V/4. So, the photoelectric equation can be written as,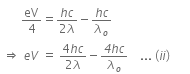
From equations (i) and (ii), we get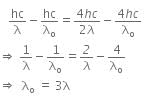
When a metallic surface is illuminated with radiation of wavelength λ stopping potential is V.
The photoelectric equation can be written as,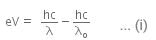
Now, when the same surface is illuminated with radiation of wavelength 2λ, the stopping potential is V/4. So, the photoelectric equation can be written as,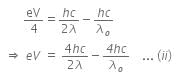
From equations (i) and (ii), we get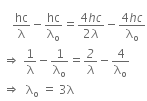
Q2: An electron of mass m and a photon have the same energy E. The ratio of de-Broglie wavelengths associated with them is:
A:
B:
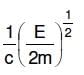
C:
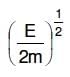
D: c(2mE)1/2
Ans: B
Given that an electron has a mass of m.
De-Broglie wavelength for an electron will be given as,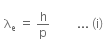
where,
h is the Planck's constant, and
p is the linear momentum of the electron
The kinetic energy of the electron is given by, 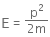
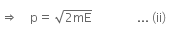
From equation (i) and (ii), we have
The energy of a photon can be given as,
Hence, λP is the de-Broglie wavelength of the photon.
Now, dividing equation (iii) by (iv), we get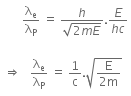
Q3: Photons with energy 5 eV are incident on a cathode C in a photoelectric cell. The maximum energy of emitted photoelectrons is 2 eV. When photons of energy 6 eV are incident on C, no photoelectrons will reach the anode A, if the stopping potential of A relative to C is
(a) + 3 V
(b) + 4 V
(c) – 1 V
(d) – 3 V
Ans: (d)
Key Idea Use Einstein’s photoelectric equation.
We know that, E = (KE)max + Work function (φ)
where, φ = hν0 E = hν
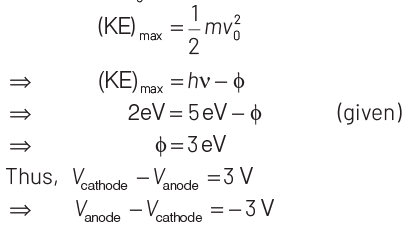
Q4: Electrons of mass m with de-Broglie wavelength λ fall on the target in an X-ray tube. The cut-off wavelength (λ 0 ) of the emitted X-ray is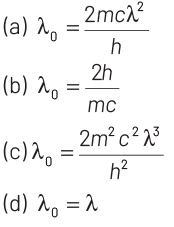
Ans: (a)
Cut-off wavelength occurs when incoming electron looses its complete energy in collision. This energy appears in the form of X-rays.
Given, mass of electrons = m
de-Broglie wavelength = λ
So, kinetic energy of electron = p2/2m
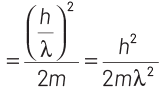
Now, maximum energy of photon can be given by
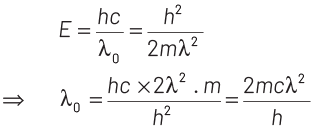
2015
Q1: A certain metallic surface is illuminated with monochromatic light of wavelength, λ. The stopping potential for photo-electric current for this light is 3V0. If the same surface is illuminated with light of wavelength 2λ, the stopping potential is V0. The threshold wavelength for this surface for the photoelectric effect is :
A: λ/6
B: 6λ
C: 4λ
D: λ/4
Ans: C
We have,
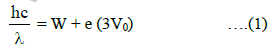
where W is the work function and (3V0) is the stopping potential when monochromatic light of wavelength λ is used.
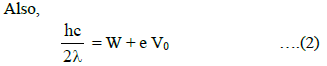
where V0 is the stopping potential when monochromatic light of wavelength 2λ is used.
Subtracting equation (2) from equation (1)
We get,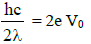
∴ 
Substituting in equation (2) we get,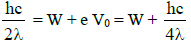
∴ 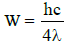
The threshold wavelength is therefore 4λ.
Q2: Which of the following figures represents the variation of the particle momentum and the associated de-Broglie wavelength?
A:
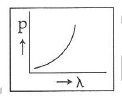
B:
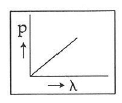
C: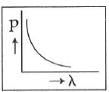
D:
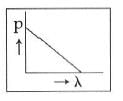
Ans: C
The de-Broglie wavelength is given by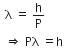
This equation is in the form of yx = c, which is the equation of a rectangular hyperbola.
The de-Broglie wavelength is given by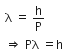
This equation is in the form of yx = c, which is the equation of a rectangular hyperbola.
(a)

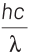
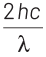
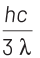
According to Einstein’s photoelectric equation,
E = Kmax + φ
where, Kmax is maximum kinetic energy of emitted electron and φ is work function of an electron.
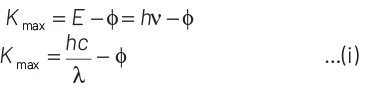
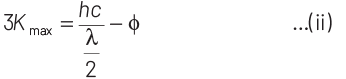
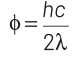
2014
Q1: When the energy of the incident radiation is increased by 20%, the kinetic energy of the photoelectrons emitted from a metal surface increases from 0.5 eV to 0.8 eV. The work function of the metal is :
A: 1.3 eV
B: 1.5 eV
C: 0.65 eV
D: 1.0 eV
Ans: D
Solution:
The original energy of the photon is E0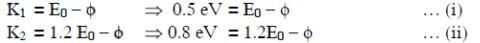
From equation (i) and (ii)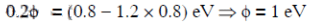
Q2: If the kinetic energy of the particle is increased to 16 times its previous value, the percentage change in the de−Broglie wavelength of the particle is :
A: 60
B: 50
C: 25
D: 75
Ans: D
Solution: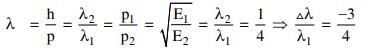
Q3: Light of wavelength 500 nm is incident on a metal with work function 2.28 eV. The de-Broglie wavelength of the emitted electron is
(a) < 2.8 × 10− 10 m
(b) < 2.8 × 10− 9 m
(c) ≥ 2.8 × 10− 9 m
(d) ≤ 2.8 × 10− 12 m
Ans: (c)
As, energy of photon, E = hν
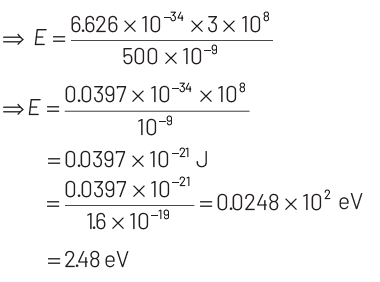
According to Einstein’s photoelectric emission, we have
KEmax = E − W = 2.48 − 2.28 = 0.2 eV
For de-Broglie wavelength of the emitted electron,
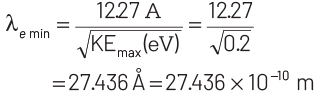
Thus, minimum wavelength of the emitted electron is
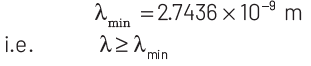
|
88 videos|421 docs|88 tests
|
FAQs on NEET Previous Year Questions (2014-2025): Dual Nature of Radiation & Matter - Physics Class 12
| 1. What is the photoelectric effect? |  |
| 2. How does the photoelectric effect support the wave-particle duality of light? |  |
| 3. What is the threshold frequency in the context of the photoelectric effect? |  |
| 4. How does the kinetic energy of emitted electrons in the photoelectric effect depend on the frequency of light? |  |
| 5. What is the significance of the work function in the photoelectric effect? |  |






















