NEET Previous Year Questions (2014-2024): Kinetic Theory | Physics Class 11 PDF Download
2023
Q1: The temperature of a gas is –50°C. To what temperature the gas should be heated so that the rms speed is increased by 3 times? [2023]
(a) 669°C
(b) 3295°C
(c) 3097 K
(d) 223 K
Ans: (b) 3295°C
Explanation:
The root mean square (RMS) speed vrms of a gas is given by the equation:
vrms = √ 3RTm
vrms ∝ √T
T1 = 273 - 50 = 223 K
vrms is increased by 3 times
T2 = ?So, final RMS speed = v + 3v = 4v
v4v = √ T1T2
√ 116 = √ 223T2
T2 = 3568 K
T2 = 3568 - 273 = 3295°C
2021
Q1: Match column - I and column - II and choose the correct match from the given choices. [2021]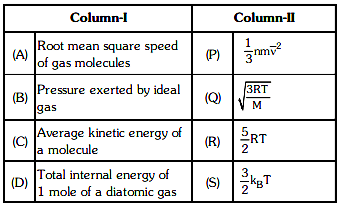
(a) (A) - (Q), (B) - (P), (C) - (S), (D) - (R)
(b) (A) - (R), (B) - (Q), (C) - (P), (D) - (S)
(c) (A) - (R), (B) - (P), (C) - (S), (D) - (Q)
(d) (A) - (Q), (B) - (R), (C) - (S), (D) - (P)
Ans: (a) (A) - (Q), (B) - (P), (C) - (S), (D) - (R)
Explanation:
- (A) Root mean square speed of gas molecules:
Root mean square (RMS) speed of gas molecules is given by the formula:
vrms = √ 3RTMHence, it matches with (Q).
- (B) Pressure exerted by an ideal gas:
The pressure exerted by an ideal gas can be represented using:
P = 13 mv2Hence, it matches with (P).
- (C) Average kinetic energy of a molecule:
The average kinetic energy per molecule is given by:
E = 32 kBTHence, it matches with (S).
- (D) Total internal energy of 1 mole of a diatomic gas:
The total internal energy for one mole of a diatomic gas is:
U = 52 RTHence, it matches with (R).
2020
Q1: A cylinder contains hydrogen gas at pressure of 249 kPa and temperature 27°C.
Its density is : (R = 8.3 J mol-1 K-1) [2020]
(a) 0.1 kg/m3
(b) 0.02 kg/m3
(c) 0.5 kg/m3
(d) 0.2 kg/m3
Ans: (d) 0.2 kg/m3
Explanation:
Concept:
Ideal Gas Equation:
The ideal gas equation represents the state of a gas and provides a good approximation of its behavior under certain conditions. It is expressed as:
PV = nRT
Where:
- P is the pressure,
- V is the volume,
- n is the number of moles of the gas,
- R is the universal gas constant, and
- T is the temperature.
Using the ideal gas equation, we have:
PV = mM RT ⟹ ρV = m ⟹ m = ρV
PV = (ρV)RTM
ρ = PMRT
Substituting the values:
ρ = 249 × 103 × 2 × 10–38.3 × 300 = 0.2 kg/m3
Q2: The mean free path for a gas, with molecular diameter d and number density n can be expressed as : [2020]
(a)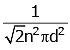
(b) 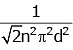
(c)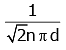
(d)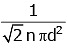
Ans: (d) 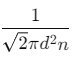
Explanation:
The mean free path for gas is given by
Q3: The average thermal energy for a mono-atomic gas is (kB is Boltzmann constant and T, absolute temperature) [2020]
(a) 1/2kBT
(b) 3/2kBT
(c) 5/2kBT
(d) 7/2kBT
Ans: (b) 3/2kBT
Explanation:
Thermal Energy
- Thermal energy refers to the energy present within a system that is responsible for its temperature.
- Thermal energy is given by the relation:
ΔET = μk F d
Where:
- μk – Coefficient of friction
- F – Force
- d – Distance
Step 1: Formula for Calculating the Average Thermal Energy
For mono-atomic gas, the total degree of freedom = 3 (translational degrees of freedom), i.e., rotational, vibrational, and translational.
The average thermal energy for a mono-atomic gas (U) is given as:
U = (total degree of freedom) × 12 KBT
Step 2: Calculating the Average Thermal Energy
By putting the value of the degree of freedom, we get:
U = 32 KBT
Hence, the average thermal energy for a mono-atomic gas is:
U = 32 KBT
2019
Q1: Increase in temperature of a gas filled in a container would lead to: [2019]
(a) Increase in its mass
(b) Increase in its kinetic energy
(c) Decrease in its pressure
(d) Decrease in intermolecular distance
Ans: (b) Increase in its kinetic energy
Explanation:
(a) Increase in its mass: The mass of the gas remains constant as temperature changes; it is not affected by temperature.
(b) Increase in its kinetic energy: As the temperature of the gas increases, the kinetic energy of the gas molecules increases because the molecules move faster at higher temperatures.
(c) Decrease in its pressure: An increase in temperature would actually lead to an increase in pressure (if the volume is constant), not a decrease.
(d) Decrease in intermolecular distance: The intermolecular distance usually increases when the temperature rises because gas molecules move faster and spread out more.
2018
Q1: At what temperature will the rms speed of oxygen molecules become just sufficient for escaping from the Earth's atmosphere ? (Given: Mass of oxygen molecule (m) = 2.76 × 10–26 kg Boltzmann's constant kB = 1.38 × 10–23 J K–1):- [2018]
(a) 2.508 × 104 K
(b) 8.360 × 104 K
(c) 5.016 × 104 K
(d) 1.254 × 104 K
Ans: (b) 8.360 × 104 K
Explanation:
Mass of oxygen molecule (m) = 2.76 × 10-26 kg
Boltzmann's constant (kB) = 1.38 × 10-23 J·K-1
Escape velocity (Vescape) = 11200 m/s
Say at temperature T, it attains Vescape.
√ 3kBTmO2 = 11200 m/s
On solving,
T = 8.360 × 104 K
2017
Q1: A gas mixture consists of 2 moles of O2 and 4 moles of Ar at temperature T. Neglecting all vibrational modes, the total internal energy of the system is:- [2017]
(a) 15 RT
(b) 9 RT
(c) 11 RT
(d) 4 RT
Ans: (c)
Explanation:
For O2 (diatomic gas):
- Oxygen (O2) is a diatomic gas. For diatomic gases, the internal energy per mole is given by:
UO2 = 52 RT per mole
- For 2 moles of O2:
UO2 = 2 × 52 RT = 5RT
For Ar (monatomic gas):
- Argon (Ar) is a monatomic gas. For monatomic gases, the internal energy per mole is given by:
UAr = 32 RT per mole
- For 4 moles of Ar:
UAr = 4 × 32 RT = 6RT
Total Internal Energy of the System:
The total internal energy is the sum of the internal energy of O2 and Ar:
Utotal = UO2 + UAr = 5RT + 6RT = 11RT
Thus, the total internal energy of the system is 11RT.
2016
Q1: The molecules of a given mass of a gas have r.m.s. velocity of 200 ms-1 at 27°C and 1.0 x 10-5 Nm-2 pressure. When the temperature and pressure of the gas are respectively, 127°C and 0.05 x 105Nm2, the r.m.s. velocity of velocity of its molecules in ms-1 is; [2016]
(a) 100 / 3
(b) 100 √2
(c) 400 / √3
(d) 100√2 / 3
Ans: (c)
Explanation:The root mean square (r.m.s.) velocity (vrms) of a gas is given by:
vrms ∝ √T
This means that the r.m.s. velocity is proportional to the square root of the absolute temperature of the gas.
Given that the initial r.m.s. velocity vrms,i = 200 m/s at an initial temperature T1 = 27°C = 300 K, we want to find the r.m.s. velocity at the new temperature T2 = 127°C = 400 K.
Using the relation:
vrms,2vrms,i = √ T2T1
Substitute the given values:
vrms,2200 = √ 400300 = √ 43
Thus:
vrms,2 = 200 × √ 43 = 200 × 2√3 = 400√3 m/s
Q2: A given sample of an ideal gas occupies a volume V at a pressure P and absolute temperature T. The mass of each molecule of the gas is m. Which of the following gives the density of the gas ? [2016]
(a) P/(kT)
(b) Pm/(kT)
(c) P/(kTV)
(d) mkT
Ans: (b) Pm/(kT)
Explanation:
We know that ideal gas equation is
PV = NkT
Where, P is the pressure
V is the volume
N is the number of molecules
k is the Boltzmann constant
T is the temperatureNow, the mass of the gas sample is given by:
M = N × m
Where m is the mass of one molecule.
The density (ρ) of the gas is:
ρ = MV = N × mV
From the ideal gas law PV = NkT, we can solve for NV (the number density):
NV = PkT
Substituting this into the density equation:
ρ = m × PkT
Thus, the density of the gas is:
ρ = PmkT
2015
Q1: The ratio of the specific heats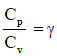 in terms of degrees of freedom (n) is given by: [2015]
in terms of degrees of freedom (n) is given by: [2015](a)
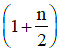
(b)

(c)
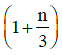
(d)
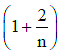
Ans: (d)
Explanation:
The ratio of the specific heats γ = CPCV is related to the degrees of freedom (n) of the gas molecules.
For a gas:
- CV(specific heat at constant volume) is given by:
CV = n2 R
- CP (specific heat at constant pressure) is related to CVas:
CP = CV + R = n2 R + R = (n + 2)2 R
Now, the ratio:
γ = CPCV = (n + 2)2 Rn2 R = n + 2n
Thus, the correct expression for γ is:
γ = 1 + 2n
Q2: Two vessels separately contain two ideal gases A and B at the same temperature, the pressure of A being twice that of B. Under such conditions, the density of A is found to be 1.5 times the density of B. The ratio of molecular weight of A and B is [2015]
(a) 2
(b) 1/2
(c) 2/3
(d) 3/4
Ans: (d) 3/4
Explanation:
According to an ideal gas equation, the molecular weight of an ideal gas is
M = ρRT / PAs:
P = ρRTM
where P, T, and ρ are the pressure, temperature, and density of the gas respectively, and R is the universal gas constant.
∴ The molecular weight of A is:
MA = ρARTAPA
and that of B is:
MB = ρBRTBPB
Hence, their corresponding ratio is:
MAMB = ρAρB × TATB × PBPA1
Here:
- ρA/ρB = 1.5 = 32
- TA/TB = 1
- PA/PB = 2
∴ MAMB = 32 × 1 × 12 = 34
2014
Q1: The mean free path of molecules of a gas,(radius ‘r’) is inversely proportional to: [2014]
(a) r
(b) √r
(c) r3
(d) r2
Ans: (d) r2
Explanation:
The mean free path (λ) of a gas molecule is the average distance a molecule travels between collisions. It is given by the formula:λ = 1√2 nπd2
Where:
- n is the number density (number of molecules per unit volume).
- d is the diameter of the gas molecule.
Since the diameter d is directly proportional to the radius r of the molecule (d = 2r), the mean free path is inversely proportional to the square of the radius (r2).
Thus, the mean free path is inversely proportional to r2.
|
97 videos|379 docs|103 tests
|
FAQs on NEET Previous Year Questions (2014-2024): Kinetic Theory - Physics Class 11
| 1. What is the Kinetic Theory of Gases? |  |
| 2. How does temperature affect the kinetic energy of gas molecules? |  |
| 3. What is the relationship between pressure and volume in gases according to the Kinetic Theory? |  |
| 4. Can the Kinetic Theory explain the behavior of real gases? |  |
| 5. How are effusion and diffusion explained by the Kinetic Theory? |  |























