Numerical Problems: Electrostatic Potential and Capacitance | Physics Class 12 - NEET PDF Download
Q1: Three point charges +2μC, -3μC, +1μC are placed at the vertices of an equilateral triangle of side 10 cm. Find the net electric potential at the centroid. (Take 1 / 4πϵ₀ = 9 × 109 Nm²/C²)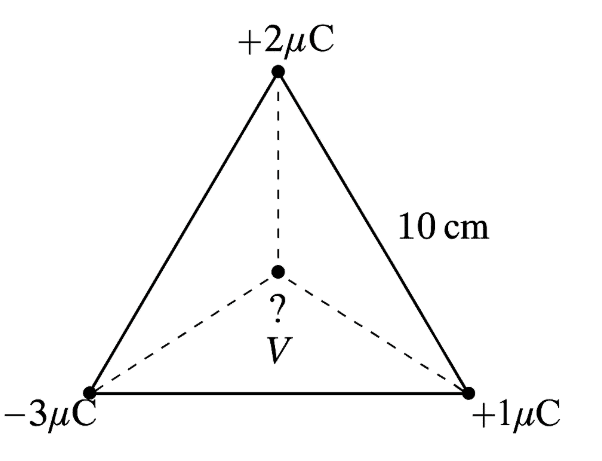
Sol: Distance from each vertex to centroid r = √3 / 3 . a = √3 / 3 . 0.1 ≈ 0.0577m
V = 9 × 109 (2 - 3 + 1) × 10-6 / 0.0577 = 0 V
Q2: Find the potential at a point P on the axial line of an electric dipole, at a distance 20 cm from its center. Dipole moment p = 6 × 10-9 C·m.
Sol: V = 1 / 4πϵ₀ . p cos θ / r², for axial line, cos θ = 1
V = 9 × 109 . 6 × 10-9 / (0.2)² = 54 / 0.04 = 1350 V
Q3: Charges +2μC and +2μC are placed 20 cm apart. A third charge -1μC is placed at the midpoint. Find total potential energy of the system.
Sol: U = Σ1 / 4πϵ₀ . qᵢqⱼ / rᵢⱼ
Total energy:
U₁₂ = 9 × 10⁹ . 2 . 2 . 10⁻¹² / 0.2 = 1.8 × 10⁻¹ J
U₁₃ = U₂₃ = 9 × 10⁹ . 2 . (-1) . 10⁻¹² / 0.1 = -1.8 × 10⁻¹ J
Utotal = 0.18 - 0.18 - 0.18 = -0.18 J
Q4: How much work is done by an external force in bringing a charge +5μC from infinity to a point where electric potential is 2 × 10³ V?
Sol: W = qV = 5 × 10⁻⁶ . 2 × 10³ = 0.01 J
Q5 : A 10μF capacitor is charged to 200 V and then disconnected. A dielectric of K = 5 is inserted. Find the new energy stored.
Sol: Initial energy:
U₀ = 1 / 2 CV² = 1 / 2 . 10⁻⁵ . (200)² = 0.2 J
New capacitance: C' = KC = 5 . 10μF = 50μF
Since charge remains constant,
U' = Q² / 2C' = (10⁻⁵ . 200)² / 2 . 50 . 10⁻⁶ = 0.04 J
Q6: Find the equivalent capacitance between A and B: Two capacitors of 6μF and 3μF in parallel, connected in series with 2μF.
Sol: Parallel: C₁ = 6 + 3 = 9μF
Now in series with 2μF:
1 / Ceq = 1 / 9 + 1 / 2 = 11 / 18 ⇒ Ceq = 18 / 11 ≈ 1.636μF
Q7: A parallel plate capacitor has Plate area (A) = 0.1 m2 ,Plate separation (d) = 2 mm = 0.002 m and partially filled with a dielectric slab of thickness d/2 (1 mm) and dielectric constant (K) = 10. Find its capacitance.
Sol: The system becomes two capacitors in series:
1. Air-filled part:
- Thickness (d1) = 1 mm = 0.001 m
- Dielectric constant (K1) = 1 (air)
2. Dielectric-filled part:
- Thickness (d2) = 1 mm = 0.001 m
- Dielectric constant (K2) = 10
The total capacitance for series combination is:
C = [ (d1 / (K1ε0A) ) + (d2 / (K2ε0A) ) ]-1
Substituting values:
C = [ (0.001 / (1 × ε0 × 0.1)) + (0.001 / (10 × ε0 × 0.1)) ]-1
C = [ (0.001 / (0.1ε0)) + (0.001 / (ε0)) ]-1
C = [ 0.01/ε0 + 0.001/ε0 ]-1
C = [ 0.011/ε0 ]-1
C = ε0 × 0.1 / 0.0011
Using ε0 ≈ 8.854 × 10-12 F/m:
C ≈ (8.854 × 10-12 × 0.1) / 0.0011
C ≈ 8.05 × 10-10 F
The capacitance is approximately 8.05 × 10-10 Farads (805 pF)
Q8: A conductor is given Charge (q) = 2 μC = 2 × 10-6 C, Radius (R) = 2 cm = 0.02 m. What is the potential at its surface?
Sol: The potential at the surface of a charged conductor is given by:
V = (1 / 4πε0) × (q / R)
Where:
- 1 / 4πε0 = 9 × 109 Nm2/C2 (Coulomb's constant)
- q = charge on conductor
- R = radius of conductor
Substituting the given values:
V = (9 × 109 Nm2/C2) × (2 × 10-6 C) / (0.02 m)
V = (9 × 109 × 2 × 10-6) / 0.02
V = (18 × 103) / 0.02
V = 9 × 105 V
The potential at the surface of the conductor is 9 × 105 Volts (900 kV)
Q9: A parallel plate capacitor has plate separation (d) = 1 mm = 10-3 m, Potential difference (V) = 100 V and area of each plate (A) = 100 cm2 = 10-2 m2. Find the force of attraction between the plates.
Sol: The force between capacitor plates is given by:
F = (1/2) × ε0 × (A × V2) / d2
Where:
- ε0 = 8.85 × 10-12 C2/Nm2 (Permittivity of free space)
- A = plate area
- V = potential difference
- d = plate separation
1. Convert all units to SI:
- 1 mm = 10-3 m
- 100 cm2 = 10-2 m2
2. Substitute values into the formula:
F = (1/2) × (8.85 × 10-12) × (10-2 × 1002) / (10-3)2
3. Simplify the expression:
F = 0.5 × 8.85 × 10-12 × (10-2 × 104) / 10-6
F = 0.5 × 8.85 × 10-12 × 102 / 10-6
F = 0.5 × 8.85 × 10-12 + 2 + 6
F = 0.5 × 8.85 × 10-4
F = 4.425 × 10-4 N
The force of attraction between the plates is 4.425 × 10-4 Newtons (0.4425 N)
Q10: An electric dipole has dipole moment (p) = 4 × 10-9 Cm placed in uniform electric field (E) = 2 × 104 N/C oriented at angle (θ) = 120°. Find the potential energy of the dipole.
Sol: The potential energy of a dipole in uniform field is given by:
U = -pE cosθ
Where:
- p = dipole moment
- E = electric field strength
- θ = angle between dipole and field
1. Substitute the given values:
U = -(4 × 10-9 Cm) × (2 × 104 N/C) × cos(120°)
2. Calculate the product of magnitudes:
pE = 4 × 10-9 × 2 × 104 = 8 × 10-5 Nm
3. Evaluate cosine term:
cos(120°) = -0.5
4. Combine all terms:
U = -8 × 10-5 × (-0.5) = 4 × 10-5 J
The potential energy of the dipole is 4 × 10-5 Joules (40 μJ).
|
88 videos|421 docs|88 tests
|
FAQs on Numerical Problems: Electrostatic Potential and Capacitance - Physics Class 12 - NEET
| 1. What is electrostatic potential, and how is it related to electric field? |  |
| 2. How do you calculate the capacitance of a parallel plate capacitor? | |
| 3. What is the energy stored in a capacitor, and how is it calculated? | |
| 4. What is the effect of dielectric materials on the capacitance of a capacitor? | |
| 5. How does the electrostatic potential vary with distance from a point charge? | |
ppt
,Free
,practice quizzes
,Semester Notes
,MCQs
,Numerical Problems: Electrostatic Potential and Capacitance | Physics Class 12 - NEET
,Exam
,video lectures
,mock tests for examination
,shortcuts and tricks
,Summary
,study material
,Numerical Problems: Electrostatic Potential and Capacitance | Physics Class 12 - NEET
,Objective type Questions
,Numerical Problems: Electrostatic Potential and Capacitance | Physics Class 12 - NEET
,past year papers
,Sample Paper
,Viva Questions
,Extra Questions
,Important questions
,Previous Year Questions with Solutions
;
Numerical Problems: Electrostatic Potential and Capacitance Free PDF Download
Importance of Numerical Problems: Electrostatic Potential and Capacitance
Numerical Problems: Electrostatic Potential and Capacitance Notes
Numerical Problems: Electrostatic Potential and Capacitance NEET Questions
Study Numerical Problems: Electrostatic Potential and Capacitance on the App
|
© EduRev
|
Education Revolution
|
|
