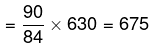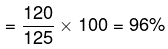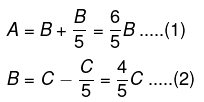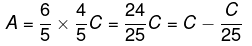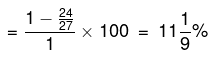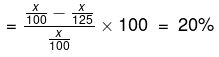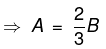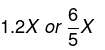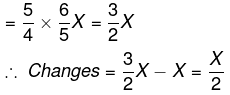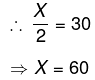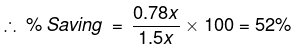Solved Examples: Percentages | CSAT Preparation - UPSC PDF Download
What is the meaning of Percent?
- The terms' percent means “for every hundred”.
- A fraction whose denominator is 100 is called percentage and the numerator of the fraction is called the rate percent.
- Thus, when we say a man made a profit of 20 percent we mean to say that he gained Rs. 20 for every hundred rupees he invested in the business, i.e. 20/100 rupees for each Rupee.
- The abbreviation of percent is p.c. and it is generally denoted by %.

Example 1. 84% of a particular total is 630 marks. What is 90% equal to?
(a) 750
(b) 675
(c) 450
(d) 550
(e) None of these
Ans. (b)
Solution.
The required answer is

Example 2. Two numbers are greater than the third number by 25% and 20% respectively. What percent of the first number is the second number?
(a) 92%
(b) 94 %
(c) 96 %
(d) 98 %
(e) None of these
Ans. (c)
Solution.
Assume the third number is 100. So the first number is 125 and the second number is 120. So the required answer is

Basics
Percentage and Fraction Equivalents
- If someone asks you to represent 50% in fractions then what will you do?
Certainly, you will come with the answer .
. - What this value actually represents? This is nothing but the fractional equivalent of the given percentage.
- From CAT point of view it is very important for us to mug up the fractional equivalent of the percentages. Some fractional equivalent are given as under:-
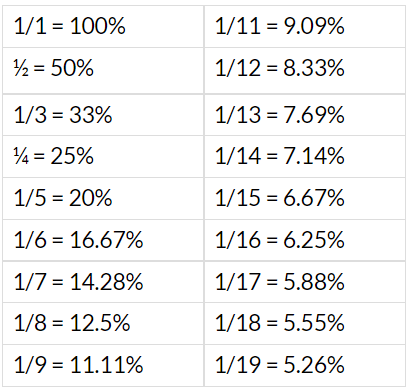
Example 3. A is earning 20% more than B, who earns 20% less than C. By what percent A earns more or less than C?
Solution.
From (1) and (2), we have
i.e A is 4% less than C.OR
Assume that ‘C’ earns 100.. Thus B earns 80 and A earn 96. So ‘A’ earns 4% less than C.
Multiplying Factor
- While dealing with %age increase or decrease picture the following scale in your mind with reference as 100% ( = 1) in the center.
 So we can say that multiplying factor (M.F) of 10% increase is 1.1 and that of 15% decrease is 0.85. An increase by x% implies the value lies on the right hand side of 100% & vice versa. Let’s start with a number X
So we can say that multiplying factor (M.F) of 10% increase is 1.1 and that of 15% decrease is 0.85. An increase by x% implies the value lies on the right hand side of 100% & vice versa. Let’s start with a number X- X increased by 10% would become
X + 0.1 X = 1.1X - X increased by 1% would become
X + 0.01 X = 1.01X - X increased by 0.1 % would become
X + 0.001 X = 1.001X - X decreased by 10% would become
X - 0.1X = 0.9X - X decreased by 1% would become
X - 0.01 X = 0.99X - X decreased by 0.1% would become
X - 0.001 X = 0.999X - X increased by 200% would become
X + 2X = 3X - X decreased by 300% would become
X - 3X = - 2X
- X increased by 10% would become
Example 4. Coconut oil is now being sold at Rs. 27 per kg. During last month its cost was Rs. 24 per kg. Find by how much percent a family should reduce its consumption, to keep the expenditure the same.
Solution. Assume the consumption last year is 1 kg, then it cost Rs. 24.
But now for Rs. 24, only 24\27 kg of oil will come. So the % reduction in consumption
Successive Percentage change
- The population of a city increases by 10% in one year and again increases by 10% in the next year, then what is the net increase in the population in two years.
- The very common answer is 20% which is wrong. Why? Let us see If Original population = P
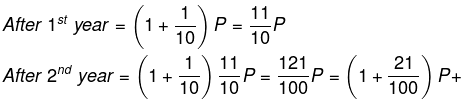
- i.e. increases by 21% of the original value.
- This successive change in the percentage can be calculated in the shortcut way as explained below:
- Let us consider a product of two quantities A = a x b.
If a & b change (increase or decrease) by a certain percentage say x & y respectively, then the overall percentage change in their product is given by the formula:
- Let us consider a product of two quantities A = a x b.
Example 5. If the volume of milk and water solution is increased by 25% by pouring water. By what percentage does the concentration of milk reduce?
Solution. Assume initially, there is 100 lts of solution, out of which x lts is milk.
So the concentration of milk is x/100.
Now it is x\125.
So percentage decrease
This formula also holds true if there are successive changes as in the case of population increase or decrease. But care has to be taken when there are either more than 2 successive changes or there is a product of more than 2 quantities as in the case of volume.
- In these cases we have to apply the same formula twice.
- If there is successive increase of x% and y%, then the net change will be

- If there is successive discount of x% and y%, then the total discount will be.

- If there is x% increase and then x% decrease, then the net change

- If the values are different, then net change

- If there is successive increase of x% and y%, then the net change will be
Example 6. If A is increased by 20% and B is decreased by 20%, then both the quantities will be equal. What percentage of B is A.
Solution. If A is increased by 20%, it will be come 1.2 A. and B is decreased by 20%, it will become 0.8 B. It is given 1.2 A = 0.8 B,
A = 0.66 B
∴ A is 66.66% of B.
Example 7. If A is 3 times to B then B is what percentage of A.
Solution. A = 3B.
⇒ B = A/3 = 0.33 A
∴ B is 33% of A.
Example 8. If ‘x’ is increased by 20% & 25% successively, then its value increases by 30. What is the value of X?
Solution. If X is increased by 20%, it will become
If it is again increased by 25%, its value becomes
It is given 30.
(or) If a value is successively increases by X% & Y%, then its value changes by
So X increases by
∴ 50% of X is given 30. ∴ X = 60.
Example 9. A man spends 30% of his salary for food and 20% of the remaining on rent and 20% of the remaining on other expenses. If he saves Rs. 8960, what is his salary?
Solution. Let his salary be ‘K’. If he spent 30% on food, he will be left with 70% of K i.e. 0.7K or
on this, he spent 20% on rent and 80 left with 80%
After spending 20% of this on other expenses he will be left with 80% of this.
i.e..
It is given as Rs. 8960.
⇒ K = 20000.
Example 10. Last year an employee used to save 40% of his salary. But now his salary is increased by 50% and expenses also increases by 20%. What is his percentage savings now?
Solution. Assume ‘X’ was the salary of the employee last year. Since his savings were 40%, his expenses were 60% i.e, 0.6X. At present, his salary is 1.5X and expenses are 1.2 (0.6X) = 0.72X
∴ Savings = 1.5 × - 0.72 = 0.78 X.
- Let us look at some examples and learn more about percentages
Example 1. In a class of 60 students, 20% are male. 75% of female students passed an exam conducted for the whole class. What is the number of female students who passed the exam.
Solution. Since it is given that 20% of students are male, that means remaining 80% are females.
Number of females- (80/100)*60= 48
Number of female students who passed= 75% of 48 = 36
Example 2. Find the approximate value of – 33.33% of 99 + 81.81% of 495.
Solution. 33.33%= 1/3 and 81.81%= 9/11
Now the problem becomes easy – 99/3 + 495*9/11= 438
Following calculations should be kept in mind
1/1= 100%
½= 50%
1/3= 33.33%
¼= 25%
1/5= 20%
1/6= 16.66%
1/7=14.28%
1/8= 12.5%
1/9= 11.11%
1/10=10%
1/11= 9.09%
1/12= 8.33% and so onThis can come in handy during certain calculations.
For example:
63.63%= (9.09*7) % = 7/11. Similarly 44.44%= 4/9 and 37.5%= 3/8.
Problems related to percentage increase or decrease form a major part.
Example 3. The wheat production increased from 50 million tons to 70 million tons. What is the percentage increase?
Solution.
Percentage Increase = (actual increase/original quantity)*100
Percentage Decrease = (actual decrease/original quantity)*100
Hence, percentage increase= (20/50)*100= 40%
Example 4. The wheat production increased by 40% on a value of 50 million tones. What is the present wheat production?
Solution. Whenever there is any percentage increase or decrease on a quantity, we can directly calculate the new value of the quantity instead of calculating the actual increase/decrease and then adding/subtracting from the original quantity
In the above question, we can say the final quantity can be calculated as
50 million * 1.4 = 70 million(Where 1.4= 1+ 0.4, 0.4 being the decimal equivalent of 40%)
On generalizing, we can say that if percentage increase is p%, then the new value is (p/100 + 1) times the old value. Conversely, if the new value is k times the old value, then the percentage increase is (k-1)*100.
Example 5. If A’s salary is 20% more than B’s salary. Then B’s salary is what percentage less then A’s salary?
Solution. Let B’s salary be 100
Hence, A’s salary = 1.2*100= 120
B’s salary is 20 less than A
The difference in percentage= (20/120)*100= 16.66%
(Note that the denominator is 120, it is because A’s salary is taken the reference point here)
Example 6. Price of a commodity increased by 30%. By what percentage should it be reduced to bring it to actual level?
Solution. let initial price = 100 (or x)
New price= 1.3*100 = 130 (or 1.3x)
Difference = 30 (or 0.3x)
The price needs to be reduced by 30 but from a reference point of 130
= (30/130)*100= 23.07% (or (0.3x/1.3x)*100)
Example 7. If my salary went up by 30% and then decreased by 30%, what is the net change?
Solution. Let my salary be x
After increase - 1.3x
After decrease - (0.7)*1.3x = 0.91x, which gives us a decrease of 9% from the original salary of x.
- Generalize, if a quantity increases by p% and then decreases by p% then there is net reduction of (p^2)/100 %.
- We have looked at all the basic examples and concepts. Let’s work out some problems.
Problem 1. If the price of sugar goes up by 10% , then what should be the percentage decrease in the quantity consumed so that the total expenditure on sugar remains the same?
Solution. Let s be the price of sugar and q be the quantity consumed. Since the price is increased by 10% , the new price is 1.1s . Let the quantity of consumption be r.
Since the total expenditure has to be the same , we get :
s * q = 1.1 s * r
hence, r = q/1.1
Percentage reduction is consumption is : ( q-q/1.1 ) * 100 / q = 100/11 %
Problem 2.
The owner of an art shop conducts his business in the following manner. Every once in a while he raises his prices by X%, then a while later he reduces all the new prices by X%. After one such up-down cycle, the price of a painting decreased by Rs.441. After a second up-down cycle, the painting was sold for Rs.1944.811. What was the original price of the painting (in Rs)?
Solution.
⇒ Let the original price be P and X%=aa2
a
Problem 3. A society had raised 60% of the amount it needed for a new building by receiving an average donation of Rs 300 from people it had already solicited. The people already solicited represent 80% of the people society intends to ask for donations. The society wants to raise the exact amount it needs for the new building. Find the average donation it should receive from the remaining people to be solicited.
Solution. Assume the amount the society needed for the new building to be A.
Let the sum of people already solicited and to be solicited be N.
60A/100 = 300 ( 80N/100) – (1)
If the average donation the society should receive from the remaining people to be solicited be x.
40A/100 = x(20N/100) -(2)
Dividing 2 by 1:
x = 800
|
208 videos|138 docs|138 tests
|
FAQs on Solved Examples: Percentages - CSAT Preparation - UPSC
| 1. What is the definition of percent? |  |
| 2. How is percent calculated? |  |
| 3. How is percent used in everyday life? |  |
| 4. What are some common examples of percent in real-life situations? |  |
| 5. How can understanding percentages be helpful in making financial decisions? |  |