Open App

UPSC Exam > UPSC Notes > CSAT Preparation > Previous Year Topic Wise Questions With Solutions: Percentages

Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC PDF Download

Q: 1. What are percentages and how are they used in daily life?

Ans. Percentages are a way of expressing a number as a fraction of 100. They are commonly used in various aspects of daily life, such as calculating discounts during shopping, understanding interest rates on loans, and analyzing data in reports. For instance, if an item is priced at 100 units and is offered at a 20% discount, the discount amount is 20 units, making the final price 80 units.

Q: 2. How do you calculate a percentage of a given number?

Ans. To calculate a percentage of a given number, you multiply the number by the percentage (expressed as a decimal). For example, to find 30% of 200, you convert 30% to decimal form, which is 0.30, and then multiply: 200 × 0.30 = 60. Thus, 30% of 200 is 60.

Q: 3. What is the difference between percentage increase and percentage decrease?

Ans. Percentage increase measures how much a value has grown relative to its original value, while percentage decrease measures how much a value has fallen. The formulas are: - Percentage Increase = [(New Value - Original Value) / Original Value] × 100- Percentage Decrease = [(Original Value - New Value) / Original Value] × 100For example, if a price rises from 50 to 75, the percentage increase is [(75 - 50) / 50] × 100 = 50%. Conversely, if it drops to 40 from 50, the percentage decrease is [(50 - 40) / 50] × 100 = 20%.

Q: 4. How can percentages be applied in financial literacy?

Ans. Percentages play a crucial role in financial literacy by helping individuals understand concepts like interest rates, taxes, and investment returns. For instance, knowing that a savings account offers 5% annual interest helps individuals evaluate where to invest their money. Furthermore, understanding how to calculate sales tax (e.g., if an item costs 100 units and tax is 10%, the total cost is 110 units) is essential for budgeting.

Q: 5. What are some common mistakes to avoid when working with percentages?

Ans. Common mistakes when working with percentages include failing to convert the percentage to a decimal before calculations, misapplying the increase or decrease formulas, and misinterpreting percentage changes. For instance, confusing a 50% increase with a 50% decrease can lead to significant errors in financial calculations. It’s also important to ensure that the base value used for percentage calculations is accurate to avoid skewed results.

Note: No questions being asked from this topic in the year 2025

Q1. A number is mistakenly divided by 4 instead of multiplying by 4. What is the percentage change in the result due to this mistake? (2024)
(a) 25%
(b) 50%
(c) 72.75%
(d) 93.75%

Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC

View Answer

Ans: (d)
Let the number be 100.
After multiplying the number by 4, the number will be 4× 100 = 400
But by mistake it was divided by 4. The resultant number will be 100/4 = 25
Required percentage change = {(400 - 25)/400} × 100 = (375/400) × 100 = 93.75%

Q2. In an examination, 80% of students passed in English, 70% of students passed in Hindi and 15% failed in both the subjects. What is the percentage of students who failed in only one subject? (2024)
(a) 15%
(b) 20%
(c) 25%
(d) 35%

View Answer

Ans: (b)
80% of students passed in English means 20% of students failed in English.
70% of students passed in Hindi means 30% of students failed in Hindi.
We can solve this question by using Venn diagram method: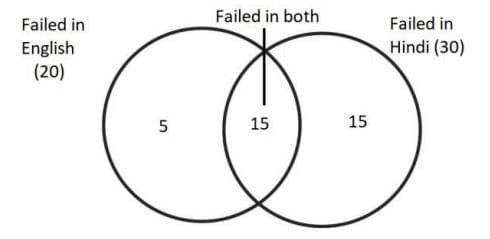
Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC Students that failed in only one subject = Students that failed in only English or those that failed in only Hindi = 5 +15 = 20%

Q3. When 70% of a number x is added to another number y, the sum becomes 165% of the value of y. When 60% of the number x is added to another number z, then the sum becomes 165% of the value of z. which one of the following is correct? (2022)
(a) z < x < y
(b) x < y < z
(c) y < x < z
(d) z < y < x

View Answer

Ans: (a)
According to the question,
0.7 x + y = 1.65 y
Or 0.7 x = 0.65 y
Or x/y = 0.65/0.70, which is less than 1.
Hence, x < y …..(i)
Now, 0.6 x + z = 1.65 z
Or 0.6 x = 0.65 z
Or x/z = 0.65/0.60, which is greater than 1.
Hence, x > z …..(ii)
From inequalities (i) and (ii), we get: z < x < y

Q4. A pie chart gives the expenditure on five different items A, B, Q D and E in a household. If B, C, D and E correspond to 90^o 50^o 45^o and 75^o respectively, then what is the percentage of expenditure on item A? (2022)
(a) 112/9
(b) 125/6
(c) 155/9
(d) 250/9

View Answer

Ans: (d)
A pie-chart corresponds to 360°.
Items B, C, D and E correspond to 90° , 50°, 45° and 75° respectively on the pie chart.
Angle corresponding to A in the pie-chart = 360° – (90° + 50° + 45° + 75°) = 100°
So, Percentage of expenditure on item A = (100/360) × 100 = (250/9)%

Q5. A pie diagram shows the percentage distribution of proteins, water and other dry elements in the human body. Given that proteins correspond to 16% and water corresponds to 70%. If both proteins and the other dry elements correspond to p%, then what is the central angle of the sector representing p on the pie diagram? (2021)
(a) 54°
(b) 96°
(c) 108°
(d) 120°

View Answer

Ans: (c)
Percentage of Other Dry Elements in the human body = 100 – (Percentage of Proteins + Percentage of Water) = 100 – (16 + 70) = 100 – 86 = 14%
The following pie-chart represents the scenario described in the question.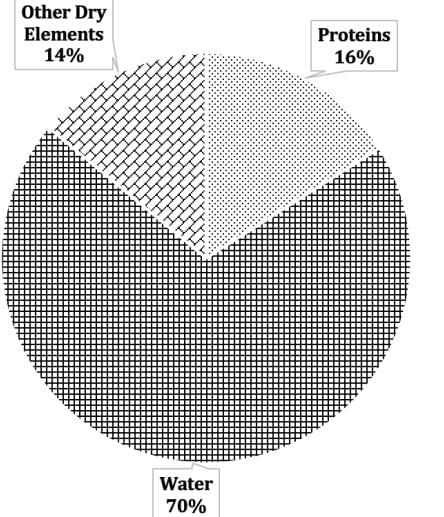
Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC

So, percentage of both Proteins and Other Dry Elements, i.e. p = 16 + 14 = 30%
In a pie diagram, 100% corresponds to 360°.
So, 30% will correspond to (360/100) × 30 = 108°
That is, the central angle of the sector representing p on the pie diagram = 108°

Q6. If the price of an article is decreased by 20% and then the new price is increased by 25%, then what is the net change in the price? (2021)
(a) 0%
(b) 5% increase
(c) 5% decrease
(d) Cannot be determined due to insufficient data

View Answer

Ans: (a)
Let the initial price be Rs. 100
New price on decreasing the original price by 20% = 100 – 20% of 100 = 100 – 20 = Rs. 80
Now, the final price on increasing the previous price by 25% = 80 + 25% of 80 = 80 + 20 = Rs. 100
So, there is no net change in price.

Q7. P scored 40 marks more than Q in an examination. If Q scored 10% less marks than P, then how much did Q score. (2021)
(a) 360
(b) 380
(c) 400
(d) 420

View Answer

Ans: (a)
P scored 40 marks more than Q. So, marks of Q are q, then the marks of P will be q + 40.
Q scored 10% less marks than P. That is, marks of Q are 90% of the marks of P.
So, q = 90% of (q + 40)
Or 10q = 9q + 360
Or q = 360
So, Q scored 360 marks.

Q8. Consider the following Table: (2021)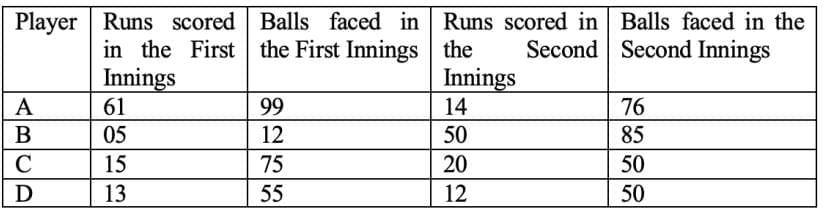
Who is the fastest run scorer in the Test Match?
(a) A
(b) B
(c) C
(d) D

View Answer

Ans: (b)
Fastest run scorer means the batsman that has the best runs scored : balls faced ratio.
Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC

For batsman A: Runs scored : Balls faced = 75/175 = 0.43
For batsman B: Runs scored : Balls faced = 55/97 = 0.57
For batsman C: Runs scored : Balls faced = 35/125 = 0.28
For batsman D: Runs scored : Balls faced = 25/105 = 0.24
The best ratio is that of batsman B.

The document Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC is a part of the UPSC Course CSAT Preparation.

All you need of UPSC at this link: UPSC

	CSAT Preparation 205 videos\|265 docs\|136 tests

CSAT Preparation

205 videos|265 docs|136 tests

Join Course for Free

FAQs on Previous Year Topic Wise Questions With Solutions: Percentages - CSAT Preparation - UPSC

1. What are percentages and how are they used in daily life?

Ans. Percentages are a way of expressing a number as a fraction of 100. They are commonly used in various aspects of daily life, such as calculating discounts during shopping, understanding interest rates on loans, and analyzing data in reports. For instance, if an item is priced at 100 units and is offered at a 20% discount, the discount amount is 20 units, making the final price 80 units.

2. How do you calculate a percentage of a given number?

Ans. To calculate a percentage of a given number, you multiply the number by the percentage (expressed as a decimal). For example, to find 30% of 200, you convert 30% to decimal form, which is 0.30, and then multiply: 200 × 0.30 = 60. Thus, 30% of 200 is 60.

3. What is the difference between percentage increase and percentage decrease?

Ans. Percentage increase measures how much a value has grown relative to its original value, while percentage decrease measures how much a value has fallen. The formulas are: - Percentage Increase = [(New Value - Original Value) / Original Value] × 100 - Percentage Decrease = [(Original Value - New Value) / Original Value] × 100 For example, if a price rises from 50 to 75, the percentage increase is [(75 - 50) / 50] × 100 = 50%. Conversely, if it drops to 40 from 50, the percentage decrease is [(50 - 40) / 50] × 100 = 20%.

4. How can percentages be applied in financial literacy?

Ans. Percentages play a crucial role in financial literacy by helping individuals understand concepts like interest rates, taxes, and investment returns. For instance, knowing that a savings account offers 5% annual interest helps individuals evaluate where to invest their money. Furthermore, understanding how to calculate sales tax (e.g., if an item costs 100 units and tax is 10%, the total cost is 110 units) is essential for budgeting.

5. What are some common mistakes to avoid when working with percentages?

Ans. Common mistakes when working with percentages include failing to convert the percentage to a decimal before calculations, misapplying the increase or decrease formulas, and misinterpreting percentage changes. For instance, confusing a 50% increase with a 50% decrease can lead to significant errors in financial calculations. It’s also important to ensure that the base value used for percentage calculations is accurate to avoid skewed results.

About this Document

4.96/5 Rating

Sep 27, 2025 Last updated

Related Exams

UPSC

Document Description: Previous Year Topic Wise Questions With Solutions: Percentages for UPSC 2025 is part of CSAT Preparation preparation. The notes and questions for Previous Year Topic Wise Questions With Solutions: Percentages have been prepared according to the UPSC exam syllabus. Information about Previous Year Topic Wise Questions With Solutions: Percentages covers topics like and Previous Year Topic Wise Questions With Solutions: Percentages Example, for UPSC 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Previous Year Topic Wise Questions With Solutions: Percentages.

Introduction of Previous Year Topic Wise Questions With Solutions: Percentages in English is available as part of our CSAT Preparation for UPSC & Previous Year Topic Wise Questions With Solutions: Percentages in Hindi for CSAT Preparation course. Download more important topics related with notes, lectures and mock test series for UPSC Exam by signing up for free. UPSC: Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC

Description

Full syllabus notes, lecture & questions for Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC - UPSC | Plus excerises question with solution to help you revise complete syllabus for CSAT Preparation | Best notes, free PDF download

Information about Previous Year Topic Wise Questions With Solutions: Percentages

In this doc you can find the meaning of Previous Year Topic Wise Questions With Solutions: Percentages defined & explained in the simplest way possible. Besides explaining types of Previous Year Topic Wise Questions With Solutions: Percentages theory, EduRev gives you an ample number of questions to practice Previous Year Topic Wise Questions With Solutions: Percentages tests, examples and also practice UPSC tests

	CSAT Preparation 205 videos\|265 docs\|136 tests

CSAT Preparation

205 videos|265 docs|136 tests

Join Course for Free

Download as PDF

Explore Courses for UPSC exam

pdf

Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC

Previous Year Questions with Solutions

past year papers

shortcuts and tricks

Important questions

practice quizzes

Extra Questions

Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC

Semester Notes

MCQs

Exam

Summary

ppt

study material

mock tests for examination

Viva Questions

Free

Objective type Questions

Previous Year Topic Wise Questions With Solutions: Percentages | CSAT Preparation - UPSC

Sample Paper

video lectures

;

Additional Information about Previous Year Topic Wise Questions With Solutions: Percentages for UPSC Preparation

Previous Year Topic Wise Questions With Solutions: Percentages Free PDF Download

The Previous Year Topic Wise Questions With Solutions: Percentages is an invaluable resource that delves deep into the core of the UPSC exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Previous Year Topic Wise Questions With Solutions: Percentages now and kickstart your journey towards success in the UPSC exam.

Importance of Previous Year Topic Wise Questions With Solutions: Percentages

The importance of Previous Year Topic Wise Questions With Solutions: Percentages cannot be overstated, especially for UPSC aspirants. This document holds the key to success in the UPSC exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Previous Year Topic Wise Questions With Solutions: Percentages Notes

Previous Year Topic Wise Questions With Solutions: Percentages Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Previous Year Topic Wise Questions With Solutions: Percentages. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Previous Year Topic Wise Questions With Solutions: Percentages Notes on EduRev are your ultimate resource for success.

Previous Year Topic Wise Questions With Solutions: Percentages UPSC

The "Previous Year Topic Wise Questions With Solutions: Percentages UPSC Questions" guide is a valuable resource for all aspiring students preparing for the UPSC exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Previous Year Topic Wise Questions With Solutions: Percentages on the App

Students of UPSC can study Previous Year Topic Wise Questions With Solutions: Percentages alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Previous Year Topic Wise Questions With Solutions: Percentages, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Previous Year Topic Wise Questions With Solutions: Percentages is prepared as per the latest UPSC syllabus.

Education Revolution