Previous Year Topic Wise Questions With Solutions: Permutation & Combination | CSAT Preparation - UPSC PDF Download
Note: No questions being asked from this topic in the year 2024 and 2025
Q1. A box contains 14 black balls, 20 blue balls, 26 green balls, 28 yellow balls, 38 red balls and 54 white balls.
Consider the following statements:
1. The smallest number n such that any n balls drawn from the box randomly must contain one full group of at least one colour is 175.
2. The smallest number m such that any m balls drawn from the box randomly must contain at least one ball of each colour is 167.
Which of the above statements is/are correct? (2023)
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2
 View Answer
View Answer 
Ans: (c)
The box contains 14 black balls, 20 blue balls, 26 green balls, 28 yellow balls, 38 red balls and 54 white balls.
Value of n
We have to find out the minimum possible number of balls that should be drawn from the box such that the balls drawn must contain one full group of at least one colour. Say, it may have all 14 black balls, or all 20 blue balls, etc.
Let’s think about the worst-case scenario. What is the maximum number of balls that we can draw without selecting a full group of any colour?
Let’s select 13 black balls, 19 blue balls, 25 green balls, 27 yellow balls, 37 red balls and 53 white balls.
These are 174 balls in total.
Now, if we select even one more ball (of any colour), it’s a certainty that at least one full group of a certain colour will get selected.
So, the value of n = 174 + 1 = 175.
So, Statement 1 is correct.
Value of m
We have to find out the minimum possible number of balls that should be drawn from the box such that the balls drawn must contain at least one ball of each colour.
Let’s think about the worst-case scenario. What is the maximum number of balls that we can draw without selecting any ball of a particular colour?
As the number of black balls is the least, we can draw the maximum possible number of balls without selecting a black ball. \
So, let’s select 20 blue balls, 26 green balls, 28 yellow balls, 38 red balls and 54 white balls.
These are 166 balls in total.
Now, only black balls are left.
So, the next ball we choose will certainly be a black ball, and we will end up having at least one ball of each colour.
So, the value of m = 166 + 1 = 167
So, Statement 2 is correct.
Hence, option (c) is correct.
Q2. How many distinct 8-digit numbers can be formed by rearranging the digits of the number 11223344 such that odd digits occupy odd positions and even digits occupy even positions? (2023)
(a) 12
(b) 18
(c) 36
(d) 72
 View Answer
View Answer 
Ans: (c)
In an eight-digit number there are 4 odd and 4 even positions.
In the number 11223344, there are 4 odd numbers (1, 1, 3, 3) and 4 even numbers (2, 2, 4, 4).
Now, the number of ways these 4 odd numbers (1, 1, 3, 3) can be arranged in 4 odd positions = 4!/(2 × 2) = 6
Similarly, the number of ways these 4 even numbers (2, 2, 4, 4) can be arranged in 4 even positions = 4!/(2 × 2) = 6
So, number of such distinct numbers = 6 × 6 = 36
Hence, option (c) is correct.
Q3. There are four letters and four envelopes and exactly one letter is to be put in exactly one envelope with the correct address. If the letters are randomly inserted into the envelopes, then consider the following statements:
1. It is possible that exactly one letter goes into an incorrect envelope.
2. There are only six ways in which only two letters can go into the correct envelopes.
Which of the statements given above is/are correct? (2023)
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2
 View Answer
View Answer 
Ans: (b)
Statement 1: If one letter is placed in an incorrect envelop, then the letter that belonged to that envelop must have also been placed in an incorrect envelop. So, it’s not possible that only one letter gets placed in an incorrect envelop. Either no letter will get misplaced, or at least two letters will get misplaced. So, Statement 1 is incorrect.
Statement 2: We need to place two letters in correct envelops and two in incorrect envelops. We can choose the two letters to be placed in correct envelops in 4C2 ways, i.e. 6 ways. The remaining two letters will automatically get chosen to get placed in each other’s envelops (i.e. incorrect envelops). So, Statement 2 is correct.
Hence, option (b) is correct.
Q4. There are five persons, P, Q, R, S and T each one of whom has to be assigned one task. Neither P nor Q can be assigned Task-1. Task-2 must be assigned to either R or S. In how many ways can the assignment be done? (2023)
(a) 6
(b) 12
(c) 18
(d) 24
 View Answer
View Answer 
Ans: (d)
There are five tasks that need to be assigned to five persons. Here two cases are possible.
Case 1: Task-2 is assigned to R
Case 2: Task-2 is assigned to S In Case 1, total number of possible ways = 2 × 1 × 3 × 2 × 1 = 12 ways
In Case 1, total number of possible ways = 2 × 1 × 3 × 2 × 1 = 12 ways
In Case 2, total number of possible ways = 2 × 1 × 3 × 2 × 1 = 12 ways
So, the assignment can be done in 12 + 12 = 24 ways.
Hence, option (d) is correct.
Q5. What is the number of selections of 10 consecutive things out of 12 things in a circle taken in the clockwise direction? (2023)
(a) 3
(b) 11
(c) 12
(d) 66
 View Answer
View Answer 
Ans: (c)
Let 12 consecutive things in the circle be x1, x2, x3, …….. x12.
We need to select 10 consecutive things out of these 12 things in the circle taken in the clockwise direction.
This selection can be made as follows:
(x1 to x10), (x2 to x11), (x3 to x12), (x4 to x1), (x5 to x2), (x6 to x3), (x7 to x4), (x8 to x5), (x9 to x6), (x10 to x7), (x11 to x8), (x12 to x9)
So, there are 12 possible ways to do so.
Hence, option (c) is correct.
Q6. The digits 1 to 9 are arranged in three rows in such a way that each row contains three digits, and the number formed in the second row is twice the number formed in the first row; and the number formed in the third row is thrice the number formed in the first row. Repetition of digits is not allowed. If only three of the four digits 2, 3, 7 and 9 are allowed to use in the first row, how many such combinations are possible to be arranged in the three rows? (2022)
(a) 4
(b) 3
(c) 2
(d) 1
 View Answer
View Answer 
Ans: (c)
We can only use three of the four digits – 2, 3, 7, and 9, in the first row.
The first digit in the first row cannot be 7 or 9, as otherwise thrice the number will not be a three-digit number.
So, the first digit in the first row can either be 2, or 3.
The possible cases are: 237, 273, 239, 293, 279, 297, 327, 372, 329, 392, 379, or 397.
On eliminating the numbers whose 3x is not a three-digit number, we are left with: 237, 273, 239, 293, 279, 297, 327, and 329.
We will check these numbers:
237 × 2 =474 (digit repetition, and so eliminated)
273 × 2 = 546; 273 × 3 = 819
239 × 2 = 478; 239 × 3 = 717 (digit repetition, and so eliminated)
293 × 2 = 586; 293 × 3 = 879 (digit repetition, and so eliminated)]
279 × 2 = 558 (digit repetition, and so eliminated)
297 × 2 = 594 (digit repetition, and so eliminated)
327 × 2 = 654; 327 × 3 = 981
329 × 2 = 658; 329 × 3 = 987 (digit repetition, and so eliminated)
So, only two cases are possible.
Q7. The letters A, B, C, D and E are arranged in such a way that there are exactly two letters between A and E. How many such arrangements are possible? (2022)
(a) 12
(b) 18
(c) 24
(d) 36
 View Answer
View Answer 
Ans: (c)
There are exactly 2 letters between A and E. So, the fifth letter must be either beside A or E.
So, the following four arrangements are possible:
A _ _ E _
_ A _ _ E
E _ _ A _
_ E _ _ A
The three blank spaces can be filled by three distinct letters in 3 × 2 × 1 = 6 ways
So, total possible arrangements = 6 × 4 = 24
Q8. One non-zero digit, one vowel and one consonant from English alphabet (in capital) are to be used in forming passwords, such that each password has to start with a vowel and end with a consonant. How many such passwords can be generated? (2022)
(a) 105
(b) 525
(c) 945
(d) 1050
 View Answer
View Answer 
Ans: (c)
One non-zero digit = 1, 2, 3, 4, 5, 6, 7, 8 or 9, i.e. 9 possible values.
There are 5 vowels and 21 consonants in English alphabet.
The password starts with a vowel and ends with a consonant. So, the digit will come at the middle.
The number of such passwords = 5 × 9 × 21 = 945
Hence, 945 such passwords can be generated
Q9. There are 9 cups placed on a table arranged in equal number of rows and columns out of which 6 cups contain coffee and 3 cups contain tea. In how many ways can they be arranged so that each row should contain at least one cup of coffee? (2022)
(a) 18
(b) 27
(c) 54
(d) 81
 View Answer
View Answer 
Ans: (d)
The cups will be arranged in a 3 × 3 matrix. 
Now, let’s consider all the possible cases.
Case 1: Each row has 2 cups of coffee and 1 cup of tea.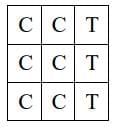
One tea cup can be placed in a row in 3 ways.
So, Possible arrangements wherein all rows have 2 coffee cups = 3 × 3 × 3 = 27 ways
Case 2: One row has 3 cups of coffee.
In such a case, one of the rows will have 2 cups of coffee and the other will have 1 cup of coffee. If the first row has 3 coffee cups, then the possible arrangements = 3 × 3 = 9 ways
If the first row has 3 coffee cups, then the possible arrangements = 3 × 3 = 9 ways
The rows having 3, 2 and 1 coffee cups can be arranged in 3! = 6 ways
So, Possible arrangements wherein one row has 3 coffee cups = 9 × 6 ways = 54 ways
Therefore, total possible arrangements = 27 + 54 = 81 ways
Hence, option (d) is the correct answer.
Q10. There are 6 persons arranged in a row. Another person has to shake hands with 3 of them so that he should not shake hands with two consecutive persons. In how many distinct possible combinations can the handshakes take place? (2021)
(a) 3
(b) 4
(c) 5
(d) 6
 View Answer
View Answer 
Ans: (b)
Method I: We just need to choose 3 persons out of 6, such that no two of them are together.
Number of ways to choose 3 out of 6 people, without any constraints = 6C3 = (6 × 5 × 4)/(3 × 2 × 1) = 20
Number of ways to choose 3 out of 6 people, such that all of them are together = 4
Number of ways to choose 3 out of 6 people, such that two of them are together = 3 + 2 + 2 + 2 + 3 = 12
So, required answer = 20 – (4 + 12) = 4
Method II:
Let the six individuals be numbered 1, 2, 3, 4, 5, and 6.
So, another person can shake hands with:
1, 3, 5
1, 4, 6
1, 3, 6
2, 4, 6
Hence, he can shake hands in 4 ways.
|
205 videos|264 docs|136 tests
|
FAQs on Previous Year Topic Wise Questions With Solutions: Permutation & Combination - CSAT Preparation - UPSC
| 1. What are permutations and combinations, and how do they differ from each other? |  |
| 2. How do you calculate the number of permutations of 'n' distinct objects taken 'r' at a time? |  |
| 3. What is the formula for calculating combinations, and how does it apply in practical scenarios? |  |
| 4. Can you explain the concept of factorial and its significance in permutations and combinations? |  |
| 5. How can permutations and combinations be applied in solving real-world problems? |  |




















