Previous Year Topic Wise Questions With Solutions: Time & Work | CSAT Preparation - UPSC PDF Download
Q1. X can complete one-third of a certain work in 6 days, Y can complete one-third of the same work in 8 days and Z can complete three-fourth of the same work in 12 days. All of them work together for n days and then X and Z quit and Y alone finishes the remaining work in 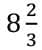 days. What is n equal to? (2025)
days. What is n equal to? (2025)
(a) 3
(b) 4
(c) 5
(d) 6
 View Answer
View Answer 
Ans: (b)
X can complete one-third of a certain work in 6 days.
So, X can complete total work in 6 × 3 = 18 days
Y can complete one-third of a certain work in 8 days.
So, Y can complete total work in 8 × 3 = 24 days
Z can complete three-fourth of a certain work in 12 days.
So, Z can complete total work in (4/3) × 12 = 16 days
Let the total amount of work be the LCM of 16, 18 and 24, i.e. 144 units
So, efficiency of X = (144/18) = 8 units/day
Efficiency of Y = (144/24) = 6 units/day
Efficiency of Z = (144/16) = 9 units/day
Efficiency of X, Y and Z together = (8 + 6 + 9) units/day = 23 units/day
Work done by Y in 26/3 days = (26/3) x 6 = 52 units
Remaining work = 144 - 52 = 92 units
Time required to complete this work when they work together = 92/23 = 4 days
So, n = 4
Q2. A set (X) of 20 pipes can fill 70% of a tank in 14 minutes. Another set (Y) of 10 pipes fills 3/8th of the tank in 6 minutes. A third set (Z) of 16 pipes can empty half of the tank in 20 minutes. If half of the pipes of set X are closed and only half of the pipes of set Y are open, and all pipes of the set (Z) are open, then how long will it take to fill 50% of the tank? (2025)
(a) 8 minutes
(b) 10 minutes
(c) 12 minutes
(d) 16 minutes
 View Answer
View Answer 
Ans: (d)
20 X pipes can fill 70% tank in 14 minutes.
So, 20 X pipes can fill 100% tank in (14/70) × 100 = 20 minutes
10 Y pipes can fill 3/8th of the tank in 6 minutes.
So, 10 Y pipes can fill 100% tank in [6/(3/8)] × 100 = 16 minutes
16 Z pipes can empty 50% tank in 20 minutes.
So, 16 Z pipes can empty 100% tank in 40 minutes.
As per the question, X and Y work at half their capacity, while Z work at full capacity.
So, Set X pipes can fill the tank in 40 minutes.
Set Y pipes can fill the tank in 32 minutes.
And, Set Z pipes can empty the tank in 40 minutes.
We can see that pipes X and Z will eliminate each other’s efforts.
So, the question boils down to this: In how much time will Y fill 50% of the tank?
As Y can fill the entire tank in 32 minutes, it will fill half the tank in 16 minutes.
Q3. A certain number of men can complete a piece of work in 6k days, where k is a natural number. By what percent should the number of men be increased so that the work can be completed in 5k days? (2024)
(a) 10%
(b) (50/3)%
(c) 20%
(d) 25%
 View Answer
View Answer 
Ans: (c)
Let the number of men in the first and second instances be m and n respectively.
So, man-days required = 6k × m = 5k × n
Or 6m = 5n Or n = (6/5)m Or n = 1.2 m
Or n = m + 20% of m
So, the number of men need to be increased by 20%.
Q4. X, Y and Z can complete a piece of work individually in 6 hours, 8 hours and 8 hours respectively. However, only one person at a time can work in each hour and nobody can work for two consecutive hours. All are engaged to finish the work. What is the minimum amount of time that they will take to finish the work. (2024)
(a) 6 hours 15 minutes
(b) 6 hours 30 minutes
(c) 6 hours 45 minutes
(d) 7 hours
 View Answer
View Answer 
Ans: (c)
X, Y and Z can complete a piece of work individually in 6 hours, 8 hours and 8 hours respectively.
Now, to finish the work in minimum possible time, we need to ensure that X is utilized the most, as he’s the most efficient worker.
So, we will use X alternatively every second hour. We will also start with him.
So, the sequence of their working will be X, (Y or Z), X, (Y or Z), X, …..and so on.
X can complete the work in 6 hours. So, in one hour he can complete 16.67% of the work.
Similarly, Y (or Z) can complete the work in 8 hours. So, in one hour he can complete 12.5% of the work.
Now, X + Y + X + Y + X + Y = 3X + 3Y = 50 + 37.5 = 87.5%
Now, 12.5% of the work is left and it’s X’s turn to do it.
X can do it in (12.5/16.67) hours, i.e. 0.75 hours, or 45 minutes.
So, the entire task can be done by them in the minimum possible time of 6 hours 45 minutes.
Q5. 24 men and 12 women can do a piece of work in 30 days. In how many days can 12 men and 24. women do the same piece of work? (2022)
(a) 30 days
(b) more than 30 days
(c) Less than 30 days or more than 30 days
(d) Data is inadequate to draw any conclusion
 View Answer
View Answer 
Ans: (d)
Since the comparative efficiencies of man and women are not known, we cannot determine the time taken by 12 men and 24 women to complete the given work.
Hence, the data is inadequate to draw any conclusion.
|
208 videos|272 docs|138 tests
|
FAQs on Previous Year Topic Wise Questions With Solutions: Time & Work - CSAT Preparation - UPSC
| 1. What is the basic concept of Time and Work in mathematics? |  |
| 2. How do you calculate the work done by multiple workers together? |  |
| 3. What is the significance of the concept of efficiency in Time and Work problems? |  |
| 4. Can you explain the concept of 'man-days' in Time and Work? |  |
| 5. What are some common types of Time and Work problems that appear in competitive exams? |  |





















