NEET Previous Year Questions (2014-2025): Motion in a Straight Line | Physics Class 11 PDF Download
2025
Q1: In some appropriate units, time (t) and position (x) relation of a moving particle is given by t = x2 + x. The acceleration of the particle is. [2025]
(a) 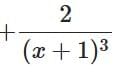
(b) 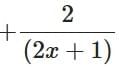
(c) 
(d) 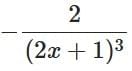
Ans: (d)
t = x2 + x
We have
dt/dx = 2x + 1
⇒ v = dx/dt = 1 / (2x + 1)
⇒ dv/dx = −2 / (2x + 1)2
⇒ a = v × dv/dx = [1 / (2x + 1)] × [−2 / (2x + 1)2]
= −2 / (2x + 1)3
Q2: Two cities X and Y are connected by a regular bus service with a bus leaving in either direction every T min. A girl is driving a scooty with a speed of 60 km/h in the direction X to Y and notices that a bus goes past her every 30 minutes in the direction of her motion, and every 10 minutes in the opposite direction. Choose the correct option for the period T of the bus service and the speed (assumed constant) of the buses. [2025]
(a) 10 min, 90 km/h
(b) 15 min, 120 km/h
(c) 9 min, 40 km/h
(d) 25 min, 100 km/h
Ans: (b) 
t1 = 30 min = 1/2 hr
t2 = 10 min = 1/6 hr
VB = speed of bus
Vg = speed of scooty (girl)
d = (VB − Vg) × t1 = (VB + Vg) × t2
⇒ (VB − 60) × 1/2 = (VB + 60) × 1/6
⇒ 3VB − 180 = VB + 60
⇒ 2VB = 240 = 120 km/h
Distance = (VB − VS) × t1
D = (120 − 60) × 1/2 = 30 km
t = d / VB = 30 / 120 = 1/4 hr = 15 min
2024
Q1: The velocity (v)− time (t) plot of the motion of a body is shown below: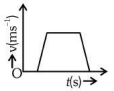 The acceleration (a)− time (t) graph that best suits this motion is : [2024]
The acceleration (a)− time (t) graph that best suits this motion is : [2024]
(a) 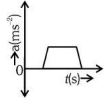
(b) 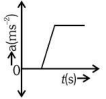
(c) 
(d) 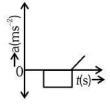
Ans: (c)
Initially, the body has zero velocity and zero slope. Hence the acceleration would be zero initially. After that, the slope of v-t curve is constant and positive.
After some time, velocity becomes constant and acceleration is zero.
After that, the slope of v-t curve is constant and negative.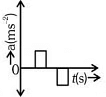
Q2: An object falls freely from height h above the ground. It travels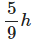 of the total height in the last 1s. The height h is: (use g = 10 m/s2) [2024]
of the total height in the last 1s. The height h is: (use g = 10 m/s2) [2024]
(a) 5 m
(b) 25 m
(c) 45 m
(d) 58 m
Ans: (c)
Let the total time taken to fall the height h be t seconds. The distance fallen in t seconds can be given by the equation:
h = (1/2) × g × t²
Now, in the last 1 second, the object travels 5/9 h of the total height. The distance fallen in the last second is the difference between the distance fallen in t seconds and the distance fallen in (t - 1) seconds. Thus, the distance fallen in the last second is:
Distance in last second = h(t) - h(t-1) = (1/2) × g × t² - (1/2) × g × (t-1)²
We are told this distance is 5/9 h. So, we can write the equation:
(1/2) × g × t² - (1/2) × g × (t-1)² = (5/9) h
Substitute g = 10 m/s²:
(1/2) × 10 t² - (1/2) × 10 × (t-1)² = (5/9) × h
Simplify:
5 × t² - 5 × (t-1)² = (5/9) × h
Factor out 5:
5 × (t² - (t-1)²) = (5/9) × h
Now expand (t-1)²:
t² - (t-1)² = t² - (t² - 2t + 1) = 2t - 1
Thus:
5 × (2t - 1) = (5/9) × h
Cancel 5 from both sides:
(2t - 1) = (1/9) × h
Now, we know the total height fallen is related to the time taken by the equation h = (1/2) × g × t²:
h = 5 t²
Substitute this in the equation:
(2t - 1) = (1/9) × 5t²
Simplify:
(2t - 1) = (5/9) × t²
Multiply through by 9 to eliminate the fraction:
9 × (2t - 1) = 5 × t²
Expand:
18t - 9 = 5t²
Rearrange into a quadratic equation:
5t² - 18t + 9 = 0
Now, solve this quadratic equation using the quadratic formula:
t = [-(-18) ± √((-18)² - 4 × 5 × 9)] / (2 × 5)
Simplify:
t = [18 ± √(324 - 180)] / 10
t = [18 ± √144] / 10
t = [18 ± 12] / 10
So, the two possible solutions for t are:
t = (18 + 12) / 10 = 30 / 10 = 3 seconds
or
t = (18 - 12) / 10 = 6 / 10 = 0.6 seconds (not physically possible)
Thus, the time t is 3 seconds.
Finding the height h:
Now, use the formula h = (1/2) × g × t²:
h = (1/2) × 10 × 3²
h = 5 × 9 = 45 meters
Thus, the height h is 45 meters.
The correct answer is (c) 45 m.
Q3: The speed (s) of a car as a function of time (t) is shown figure, The distance travelled by the car in 8 seconds is: [2024]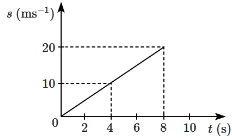 (a)180m
(a)180m
(b) 60m
(c) 80m
(d) 18m
Ans: (c)
Assume the speed-time graph is either a straight line or a series of geometric shapes. We will consider a possible case where the graph is linear (i.e., the speed increases linearly over time). This is a common type of question.
- Speed-time graph: If the graph shows a linear increase in speed from 0 m/s to V over t = 8 seconds, the graph will be a right triangle. The base of the triangle will be 8 seconds (time), and the height will be V (the maximum speed after 8 seconds).
- Distance traveled = Area under the speed-time graph. If the graph is a triangle:
Area of a triangle = (1/2) × base × height
Here, the base = 8 seconds and the height = V m/s (maximum speed). - The distance traveled = (1/2) × 8 × V = 4V meters.
Finding the speed V:
Since the maximum speed is not given directly, we can infer it from the answer choices. If we assume that the maximum speed V is 20 m/s, then the distance traveled would be:
Distance traveled = 4 × 20 = 80 meters.
Thus, the distance traveled by the car in 8 seconds is 80 meters, which corresponds to the answer (c) 80m.
Q4: A particle is moving along the x-axis with its position (x) varying with time (t) as x = αt4 + βt2 + γt + δ. The ratio of its initial velocity to its initial acceleration is: [2024]
(a) 2 α : δ
(b) γ : 2δ
(c) 4 α : β
(d) γ : 2β
Ans: (d)
The position of the particle as a function of time is given by:
x = αt⁴ + βt² + γt + δ
To find the ratio of the initial velocity to the initial acceleration, we need to first calculate the initial velocity and initial acceleration.
Step 1: Initial Velocity
The velocity of the particle is the first derivative of the position function with respect to time t:
v(t) = dx/dt
Differentiate the position function:
v(t) = d/dt [αt⁴ + βt² + γt + δ]
Using basic differentiation rules:
v(t) = 4αt³ + 2βt + γ
The initial velocity is the velocity at t = 0, so substitute t = 0 into the velocity equation:
v(0) = 4α(0)³ + 2β(0) + γ = γ
So, the initial velocity is γ.
Step 2: Initial Acceleration
The acceleration of the particle is the first derivative of the velocity function with respect to time t:
a(t) = dv/dt
Differentiate the velocity function:
a(t) = d/dt [4αt³ + 2βt + γ]
Using basic differentiation rules:
a(t) = 12αt² + 2β
The initial acceleration is the acceleration at t = 0, so substitute t = 0 into the acceleration equation:
a(0) = 12α(0)² + 2β = 2β
So, the initial acceleration is 2β.
Step 3: Ratio of Initial Velocity to Initial Acceleration
Now, we need to find the ratio of the initial velocity to the initial acceleration:
(Initial velocity) / (Initial acceleration) = γ / 2β
Thus, the ratio is γ : 2β.
The correct answer is (d) γ : 2β.
2023
Q1: A vehicle travels half the distance with speed v and the remaining distance with speed 2v. Its average speed is [2023]
(a) V/3
(b) 2V/3
(c) 4V/3
(d) 3V/4
Ans: (c)
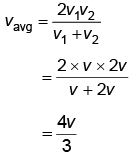
Q2: A bullet from a gun is fired on a rectangular wooden block with velocity u. When bullet travels 24 cm through the block along its length horizontally, velocity of bullet becomes u/3. Then it further penetrates into the block in the same direction before coming to rest exactly at the other end of the block. The total length of the block is [2023]
(a) 27 cm
(b) 24 cm
(c) 28 cm
(d) 30 cm
Ans: (a)
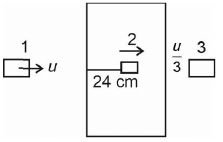
between 1 to 2
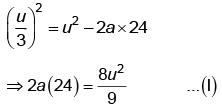
between 2 to 3
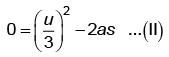
From equation (I) and (II)
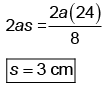
Length of wooden block is 24 + 3 = 27 cm
Q4: A horizontal bridge is built across a river. A student standing on the bridge throws a small ball vertically upwards with a velocity 4 m s–1. The ball strikes the water surface after 4 s. The height of bridge above water surface is (Take g = 10 m s–2) [2023]
(a) 56 m
(b) 60 m
(c) 64 m
(d) 68 m
Ans: (c)
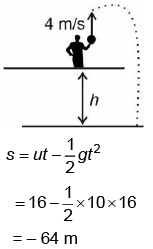
Height of bridge above water surface = 64 m
2022
Q1: The position-time (x - t) graph for positive acceleration is
(a) 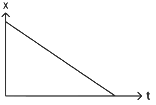
(b) 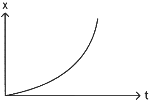
(c) 
(d) 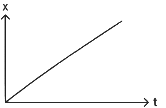
Ans: (b)
Slope of position-time (x - t) graph represents velocity.
In graph-2, the slope is increasing hence the velocity is increasing hence acceleration is positive.
Q2: The ratio of the distances travelled by a freely falling body in the 1st, 2nd, 3rd, and 4th second [2022]
(a) 1 : 4 : 9 : 16
(b) 1 : 3 : 5 : 7
(c) 1 : 1 : 1 : 1
(d) 1 : 2 : 3 : 4
Ans: (b)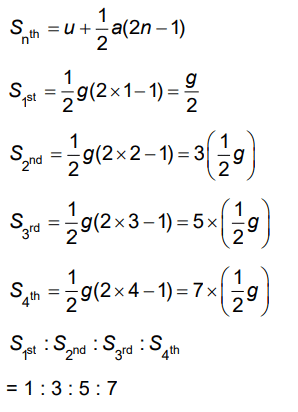
Q3: The displacement-time graphs of two moving particles make angles of 30° and 45° with the x-axis as shown in the figure. The ratio of their respective velocity is [2022]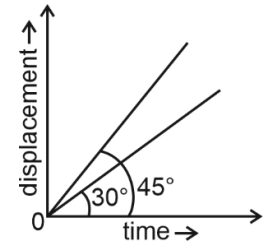 (a) 1 : 1
(a) 1 : 1
(b) 1 : 2
(c) 1: √3
(d) √3 : 1
Ans: (c)
Slope of x-t curves gives the velocity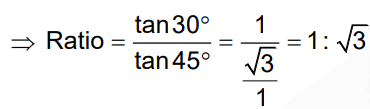
2021
Q1: A small block slides down on a smooth inclined plane starting from rest at time t=0. Let Sn be the distance travelled by the block in the interval t= n-1 to t=n. Then the ratio 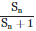 is: [2021]
is: [2021]
(a) 
(b) 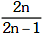
(c) 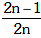
(d) 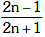
Ans: (d)
Sn = Distance in nth sec.
i.e. t = n – 1 to t = n
Sn + 1 = Distance in (n + 1)th sec.
i.e. t = n to t = n + 1
So as we know,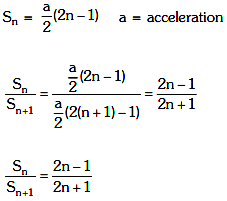
2020
Q1: A ball is thrown vertically downward with a velocity of 20m/s from the top of a tower. It hits the ground after some time with a velocity of 80m/s. The height of the tower is : (g = 10m/s2) [2020]
(a) 320 m
(b) 300 m
(c) 360 m
(d) 340 m
Ans: (b)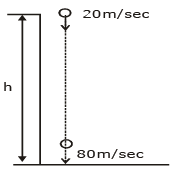
v2 – u2 = 2as
(80)2 – (–20)2 = 2(–10) × s
6400 – 400 = 2 × (–10) × s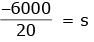
s = – 300 m
Height of tower h = 300 m
2019
Q1: The speed of a swimmer in still water is 20 m/s. The speed of river water is 10 m/s and is flowing due east. If he is standing on the south bank and wishes to cross the river along the shortest path, the angle at which he should make his strokes w.r.t. north is given by :
(a) 0o
(b) 60
(c) 45o west
(d) 30o west
Ans: (d)
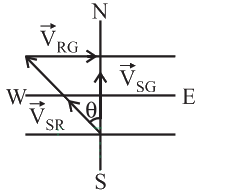
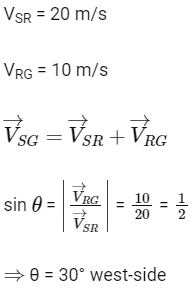
2017
Q1: Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time t1. On other days, if she remains stationary on the moving escalator, then the escalator takes her up in time t2. The time taken by her to walk up on the moving escalator will be [2017]
(a) 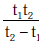
(b) 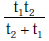
(c) t1 – t2
(d) 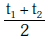
Ans: (b)
Solution: Given:
- t1: Time taken by Preeti to walk up the stationary escalator.
- t2: Time taken by the escalator to carry Preeti up when she remains stationary.
Let vP be Preeti’s walking speed, and vE be the escalator’s speed.
Preeti's walking speed can be written as:
vP = d / t1
The escalator's speed is:
vE = d / t2
When Preeti walks on the moving escalator, her effective speed is the sum of her walking speed and the escalator’s speed:
Effective speed = vP + vE
The time taken by Preeti to walk up the moving escalator is:
t = d / (vP + vE)
Substituting the expressions for vP and vE, we get:
t = d / (d / t1 + d / t2)
Simplifying the expression:
t = 1 / (1 / t1 + 1 / t2)
Therefore, the time taken by Preeti to walk up the moving escalator is:
t = (t1 t2) / (t1 + t2)
2016
Q1: A particle moves so that its position vector is given by r = cosωtx + sinωty. Where ω is a constant. Which of the following is true?
(a) Velocity is perpendicular to r and acceleration is directed away from the origin.
(b) Velocity and acceleration both are perpendicular to r
(c) Velocity is acceleration both are parallel to r
(d) Velocity is perpendicular to r and acceleration is directed towards the origin. [2016]
Ans: (d)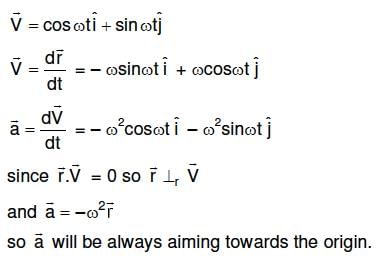
Q3: If the velocity of a particle is  , where A and B are constants, then the distance travelled by it between 1s and 2s is [2016]
, where A and B are constants, then the distance travelled by it between 1s and 2s is [2016]
(a) A/2 + B/3
(b) 3A/2 + B
(c) 3A + 7B
(d) 3A/2 + 7B/3
Ans: (d)
2015
Q1: A particle of unit mass undergoes one-dimensional motion such that its velocity varies according to v(x) = βx-2n, where β and n are constants and x is the position of the particle. The acceleration of the particle as a function of x, is given by :
[NEET / AIPMT 2015 Cancelled Paper ]
(a) -2nβ2 e-4n + 1
(b) -2nβ2 x-2n - 1
(c) -2nβ2 x-4n - 1
(d) -2nβ2 x-2n + 1
Ans: (c)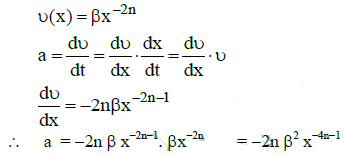
|
96 videos|367 docs|98 tests
|
FAQs on NEET Previous Year Questions (2014-2025): Motion in a Straight Line - Physics Class 11
| 1. What is the equation for motion in a straight line? |  |
| 2. How is velocity related to displacement in motion in a straight line? |  |
| 3. What is the difference between speed and velocity in motion in a straight line? |  |
| 4. How does acceleration affect motion in a straight line? |  |
| 5. What are the different types of motion in a straight line? |  |

















