NEET Exam > NEET Notes > NCERT Exemplar & Revision Notes for NEET > Revision Notes: Gravitation & Projectile
Gravitation & Projectile Class 11 Notes Physics
Gravitation:-
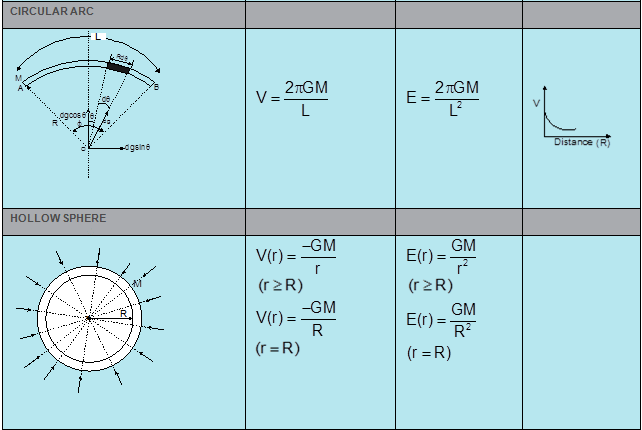
- Kepler’s first law (law of elliptical orbit):- A planet moves round the sun in an elliptical orbit with sun situated at one of its foci.
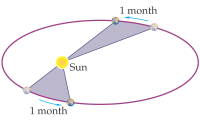
- Kepler’s second law (law of areal velocities):- A planet moves round the sun in such a way that its areal velocity is constant.
- Kepler’s third law (law of time period):- A planet moves round the sun in such a way that the square of its period is proportional to the cube of semi major axis of its elliptical orbit.
 T2 ∝ R3
T2 ∝ R3
Here R is the radius of orbit.
T2 = (4π2/GM)R 3 - Newton’s law of gravitation:-
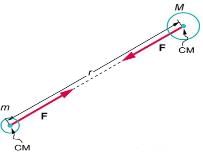
Every particle of matter in this universe attracts every other particle with a forcer which varies directly as the product of masses of two particles and inversely as the square of the distance between them.
F= GMm/r2
Here, G is universal gravitational constant. G = 6.67 ´10 -11 Nm2 / kg2 - Dimensional formula of G: G = Fr2/Mm =[MLT-2][L2]/[M2] = [M-1L3T-2]
- Acceleration due to gravity (g):- g = GM/R2
- Variation of g with altitude:- g' = g(1- 2h/R), if h<<R. Here R is the radius of earth and h is the height of the body above the surface of earth.
- Variation of g with depth:- g' = g(1- d/R). Here g' be the value of acceleration due to gravity at the depth d.
- Variation with latitude:-
At poles:- θ = 90°, g' = g
At equator:- θ = 0°, g' = g (1-ω2R/g)
Here ω is the angular velocity. - As g = GMe/Re2 , therefore gpole > gequator
- Gravitational Mass:- m = FR2/GM
- Gravitational field intensity:-
E = F/m
= GM/r2 - Weight:- W= mg
- Gravitational intensity on the surface of earth (Es):-
Es = 4/3 (πRρG)
Here R is the radius of earth, ρ is the density of earth and G is the gravitational constant. - Gravitational potential energy (U):- U = -GMm/r
(a) Two particles: U = -Gm1m2/r
(b) hree particles: U = -Gm1m2/r12 – Gm1m3/r13 – Gm2m3/r23 - Gravitational potential (V):- V(r) = -GM/r
At surface of earth,
Vs= -GM/R
Here R is the radius of earth. - Escape velocity (ve):-
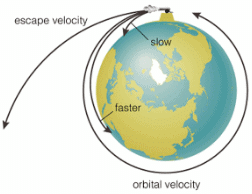
It is defined as the least velocity with which a body must be projected vertically upward in order that it may just escape the gravitational pull of earth.
ve = √2GM/R
or, ve = √2gR = √gD
Here R is the radius of earth and D is the diameter of the earth. - Escape velocity (ve) in terms of earth’s density:- ve = R√8πGρ/3
- Orbital velocity (v0):-
v0 = √GM/r
If a satellite of mass m revolves in a circular orbit around the earth of radius R and h be the height of the satellite above the surface of the earth, then,
r = R+h
So, v0 = √MG/R+h = R√g/R+h
In the case of satellite, orbiting very close to the surface of earth, then orbital velocity will be,
v0 = √gR - Relation between escape velocity ve and orbital velocity v0 :- v0= ve/√2 (if h<<R)
- Time period of Satellite:- Time period of a satellite is the time taken by the satellite to complete one revolution around the earth.
T = 2π√(R+h)3/GM = (2π/R)√(R+h)3/g
If h<<R, T = 2π√R/g - Height of satellite:- h = [gR2T2/4π2]1/3 – R
- Energy of satellite:-
Kinetic energy, K = ½ mv02 = ½ (GMm/r)
Potential energy, U = - GMm/r
Total energy, E = K+U
= ½ (GMm/r) + (- GMm/r)
= -½ (GMm/r) - Gravitational force in terms of potential energy:- F = – (dU/dR)
- Acceleration on moon:-
gm = GMm/Rm2 = 1/6 gearth
Here Mm is the mass of moon and Rm is the radius of moon. - Gravitational field:-
(a) Inside:-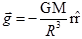
(b) Outside:-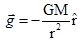
- GRAVITATIONAL POTENTIAL & FIELD DUE TO VARIOUS OBJECTS

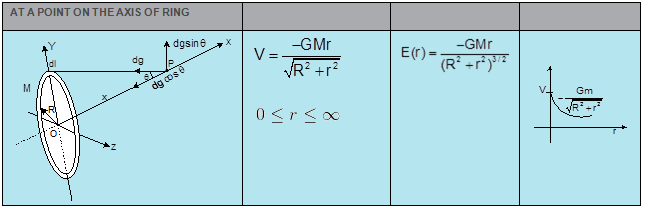
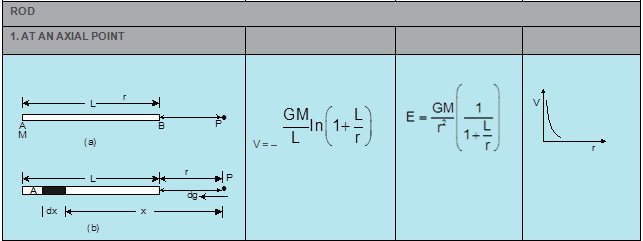
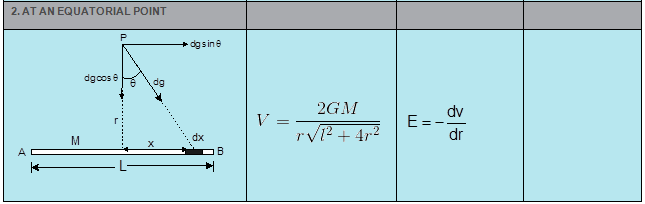


Projectile:-
- Projectile fired at angle α with the horizontal:- If a particle having initial speed u is projected at an angle α (angle of projection) with x-axis, then,
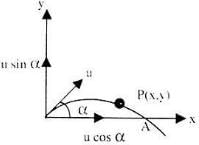
Time of Ascent, t = (u sinα)/g
Total time of Flight, T = (2u sinα)/g
Horizontal Range, R = u2sin2α/g
Maximum Height, H = u2sin2α/2g
Equation of trajectory, y = xtanα-(gx2/2u2cos2α)
Instantaneous velocity, V=√(u2+g2t2-2ugt sinα)
and
β = tan-1(usinα-gt/ucosα) - Projectile fired horizontally from a certain height:-
Equation of trajectory: x2 = (2u2/g)y
Time of descent (timer taken by the projectile to come down to the surface of earth), T = √2h/g
Horizontal Range, H = u√2h/g. Here u is the initial velocity of the body in horizontal direction.
Instantaneous velocity:-
V=√u2+g2t2
If β be the angle which V makes with the horizontal, then,
β = tan-1(-gt/u) - Projectile fired at angle α with the vertical:-
Time of Ascent, t = (u cosα)/g
Total time of Flight, T = (2u cosα)/g
Horizontal Range, R = u2sin2α/g
Maximum Height, H = u2cos2α/2g
Equation of trajectory, y = x cotα-(gx2/2u2sin2α)
Instantaneous velocity, V=√(u2+g2t2-2ugt cosα) and β = tan-1(ucosα-gt/usinα) - Projectile fired from the base of an inclined plane:-
Horizontal Range, R = 2u2 cos(α+β) sinβ/gcos2α
Time of flight, T = 2u sinβ/ gcosα
Here, α+β=θ
The document Gravitation & Projectile Class 11 Notes Physics is a part of the NEET Course NCERT Exemplar & Revision Notes for NEET.
All you need of NEET at this link: NEET
FAQs on Gravitation & Projectile Class 11 Notes Physics
| 1. What is the formula for calculating the force of gravity? |  |
Ans. The formula for calculating the force of gravity is given by Newton's law of universal gravitation, which states that the force is equal to the product of the masses of two objects divided by the square of the distance between them, multiplied by the gravitational constant. Mathematically, it can be represented as F = (G * m1 * m2) / r^2, where F is the force of gravity, G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between their centers of mass.
| 2. How does the force of gravity affect the motion of objects? |  |
Ans. The force of gravity affects the motion of objects by causing them to accelerate towards each other. According to Newton's second law of motion, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. As gravity exerts a force on an object, it causes it to accelerate towards the center of the gravitational field. This acceleration is commonly referred to as "falling" and is responsible for the motion of objects on the surface of the Earth and other celestial bodies.
| 3. What is projectile motion? |  |
Ans. Projectile motion refers to the motion of an object that is launched into the air and then moves along a curved path under the influence of gravity. In this type of motion, the object is subject to two independent motions: horizontal motion and vertical motion. The horizontal motion is constant and is not affected by gravity, while the vertical motion is influenced by gravity and follows a parabolic trajectory. Examples of projectile motion include a ball thrown into the air and a bullet fired from a gun.
| 4. How is the range of a projectile calculated? |  |
Ans. The range of a projectile is the horizontal distance it travels before hitting the ground. It can be calculated using the formula R = (v^2 * sin(2θ)) / g, where R is the range, v is the initial velocity of the projectile, θ is the angle of projection, and g is the acceleration due to gravity. This formula takes into account the horizontal component of the initial velocity and the effect of gravity on the vertical motion of the projectile.
| 5. What factors affect the trajectory of a projectile? |  |
Ans. Several factors affect the trajectory of a projectile, including the initial velocity, angle of projection, and the presence of air resistance. The initial velocity determines the speed at which the projectile is launched, while the angle of projection determines the direction of the initial velocity vector. These two factors combined determine the shape and range of the projectile's trajectory. Additionally, air resistance can also affect the trajectory by slowing down the projectile's motion and altering its path. However, in ideal projectile motion problems, air resistance is often neglected.
Related Searches





















